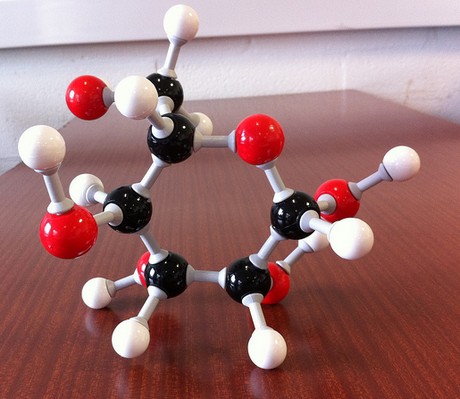
yhdisteen empiirinen kaava kertoo, että pienin kokonaislukusuhde kyseisen yhdisteen muodostavien alkuaineiden välillä on.

tämä tarkoittaa, että empiirisen kaavan voi ajatella olevan eräänlainen molekyylin rakennusosa.

kun tarkastellaan yhdisteesi empiiristä kaavaa #”CH”_2″O”#, tiedät tarvitsevasi

• yhden hiiliatomin
• kaksi vetyatomia

voidakseen alkaa rakentaa tätä molekyyliä. Teidän tehtävänne on nyt selvittää, montako rakennuspalikkaa tarvitaan yhdisteen molekyylikaavan saamiseksi.

huomaa, että tiedät yhdisteen moolimassan. Moolimassa kertoo, mikä on yhdisteen yhden moolin kokonaismassa.

tämä tarkoittaa sitä, että jos selvittää rakennuspalikan moolimassan, voi molekyylin koko moolimassan avulla määrittää, kuinka monta rakennuspalikkaa tarvitsee.

saadakseen empiirisen kaavan moolimassan käytetään jokaisen sen sisältämän atomin moolimassoja

#overbrace(1 xx ”12.011 g/mol”)^(Väri(Sininen)(”yksi mooli C”)) + overbrace(2 xx ”1.00794 g/mol”)^(Väri(Vihreä)(”kaksi moolia H”)) + overbrace(1 xx ”15.9994 g/mol”)^(Väri(Punainen)(”yksi mooli o”)) = ”30.03 g/mol”#

joten yhden rakennuspalikan moolimassa on #”30.03 g/mol”# ja molekyylin moolimassa on #”180.2 g / mol”#. Tämä tarkoittaa, että sinulla on

# 30.03 color(red)(cancel(color(black)(”g/mol”)) * color(blue) (n) = 180.2 color(red) (cancel(color(black) (”g/mol”)))#

#color(blue) (n) = 180.2/30.03 = 6.0007 ~~ 6#

The molecular formula of the compound will thus be

#(”CH”_2″O”)_color(blue)(6) implies ”C”_6″H”_12″O”_6 -># glucose