Il y a plus d’une façon de additionner une série infinie. La sommation de Cesàro vous permet de calculer la somme de séries qui n’ont pas de somme au sens classique.
Supposons que nous ayons une série infinie
La nième somme partielle de la série est donnée par
La somme classique de la série, si elle existe, est définie comme la limite de ses sommes partielles. Autrement dit,
La sommation de Cesàro adopte une approche différente. Au lieu de prendre la limite des sommes partielles, il prend la limite des moyennes des sommes partielles. Pour être précis, définissez
et définissez la somme de Cesàro comme étant la limite du Cn lorsque n va à l’infini. Si une série a une somme au sens classique, elle a aussi une somme au sens de Cesàro, et les limites sont les mêmes. Mais certaines séries ont une somme de Cesàro qui n’ont pas de somme classique. Ou peut-être que les deux limites existent, mais les étapes intermédiaires de la sommation de Cesàro se comportent mieux, comme nous le verrons dans un exemple ci-dessous.
Si vous exprimez le Cn en termes des termes an originaux, vous obtenez
En d’autres termes, la nième somme partielle de Cesàro est une re-pondération des sommes partielles classiques, les poids changeant en fonction de n. Notez que pour i fixe, la fraction multipliant ai passe à 1 lorsque n augmente.
Sommation de Fejér et phénomène de Gibbs
La sommation de Fejér est une sommation de Cesàro appliquée aux séries de Fourier. Les sommes partielles (ordinaires) d’une série de Fourier donnent la meilleure approximation d’une fonction mesurée par la norme des moindres carrés. Mais les sommes partielles de Cesàro peuvent être qualitativement plus semblables à la fonction approchée. Nous le démontrons ci-dessous avec une onde carrée.
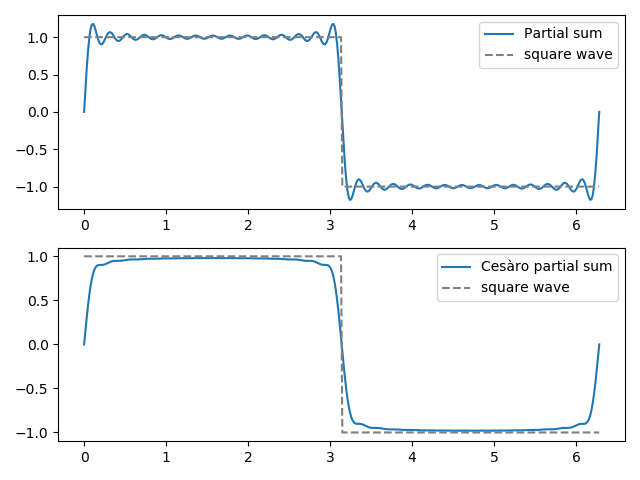
La 30ème somme partielle ordinaire montre les débuts du phénomène de Gibbs, les « oreilles de chauve-souris » en haut de l’onde carrée et leur image miroir en bas. La 30e somme partielle de Cesàro est plus lisse et élimine les phénomènes de Gibbs près de la discontinuité dans l’onde carrée.
Autres articles de la série de Fourier
- Série de Fourier-Bessel
- Contre-exemple du principe de Dirichlet
- Ondes sinusoïdales coupées
