Faisons ceci. Je vais dériver l’expression du centre de masse d’un triangle rectangle. Pourquoi?

Voyez, nous allons nous amuser. J’ai déjà inclus un mème Yoda. Qu’est-ce qui pourrait mal tourner?

Voici le triangle.

Oh, ressemble à un triangle bleu normal. Pas vrai? Mais supposons qu’il s’agisse d’une fine feuille de métal d’une masse de M. Comment trouveriez-vous l’emplacement du centre de masse? Commençons par la définition de base du centre de masse.

Il s’agit essentiellement d’une moyenne pondérée. OK, c’EST une moyenne pondérée. Mais si vous cassez l’objet en un tas de minuscules morceaux, multipliez la position vectorielle de chaque masse et sa masse minuscule. Ensuite, vous ajoutez puis tout et divisez par la masse totale. C’est le centre de masse. Voici une autre photo.

Bien sûr, dans ce cas, nous n’avons pas un tas de pièces. Nous avons une masse continue. Cela signifie que nous pouvons à la place transformer la somme en une intégrale. Au lieu de traiter à la fois les directions x et y en même temps, je vais simplement considérer le centre de masse y.

Je vais commencer par diviser ce triangle en un tas de rectangles horizontaux. Voici un de ces rectangles.

Donc, je peux utiliser ces rectangles maigres pour trouver le centre de masse. J’ai juste besoin de multiplier la position de chaque rectangle et la masse de chaque rectangle. La position est assez simple, c’est « y ». La masse est un peu plus délicate. Notez également que pour les rectangles qui remontent le triangle, ils sont plus petits avec une masse plus petite.

L’aire de ce petit rectangle doit être proportionnelle à son aire. Permettez-moi de définir la densité de surface pour l’ensemble du triangle comme suit:

Cela signifie que la masse du petit rectangle sera la valeur minuscule (dm) qui dépend de son aire.

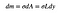
Enfin, je dois obtenir L en termes de y. Je vais le faire en obtenant d’abord une expression en termes de x. Je peux appeler le côté gauche du rectangle « x » et le côté droit « s ». Cela signifie que :

Mais le côté gauche de ce triangle peut être décrit comme une droite avec l’équation :

>

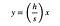
Où (h/s) est la pente. Je peux résoudre cette équation pour x et la remplacer par l’expression pour L.

Que diriez-vous d’une vérification rapide de la réalité. Faisons en sorte que les choses fonctionnent avant d’aller trop loin. Et si on laissait y =h ? Cela devrait être au sommet du triangle avec une longueur de rectangle de zéro. Ouaip. Ça marche. Qu’en est-il de y = 0? Le rectangle doit avoir une longueur de s. A l’air bien.

Maintenant, j’ai juste besoin de mettre tout cela ensemble. C’est la masse de cette tranche d’un rectangle.

Le « s » annule FTW (pour la victoire).

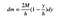
C’est assez bon pour l’instant. L’étape suivante consiste à écrire une expression pour le centre de masse y. Puisque je vais laisser la largeur de cette pièce aller à zéro, je vais obtenir une intégrale au lieu d’une somme.

Je peux l’intégrer, mais c’est plus facile si je le divise en deux parties. Juste un peu d’algèbre me donne:

>

Maintenant je peux intégrer. Voici ce que j’ai.

Évaluation aux limites (ce qui est facile puisque la limite inférieure est nulle) :

Boom. C’est le centre de masse y. Il a même des unités de distance (ce qu’il devrait). Notez également que le centre de masse y ne dépend pas de la longueur du triangle dans la direction x (le paramètre s). C’est cool. Cela signifie également que nous pouvons facilement trouver le centre de masse x. Tout ce que je dois faire est de casser ce même triangle en rectangles verticaux.

Afin de rendre les calculs identiques dans la direction X, je devrais déplacer l’origine vers l’autre coin du triangle. Cela signifie que le centre de masse x est (1/3) s du côté droit. Cela donne un centre de masse total de :

Refroidir.

Calcul numérique du Centre de masse

Oh, vous pensiez que j’avais fini? Je n’ai pas fini. Que diriez—vous de cela – un calcul numérique du centre de masse? Oui, ce sera amusant. Voici mon plan.

• Choisissez les dimensions réelles d’un triangle. Je ne peux pas faire de calcul numérique avec des variables. J’ai besoin de chiffres. Je vais utiliser s = 4, h = 1. Oui, il devrait y avoir des unités, mais peu importe. OK, la densité de surface est de 1 (il devrait être clair que cela n’a pas non plus d’importance).
• Choisissez une petite taille de pas. Disons que j’ai de petits blocs d’une taille de 0,01 par 0,01. Trouvez l’emplacement vectoriel de ce bloc et sa masse (tous les blocs ont la même masse).
• Utilisez la version de la formule somme du centre de masse.
• Déplacez le bloc jusqu’à ce que toutes les parties du triangle soient couvertes.

Faisons cela. OK, il y a une petite difficulté. Je vais devoir faire une boucle dans une boucle. La boucle interne additionnera des carrés le long de l’axe des abscisses à partir de la pente gauche jusqu’à x = h. La boucle externe déplacera ces lignes horizontales de 0 à h.

Voici la partie principale du code (code complet ici):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

Avec une taille de pièce de 0,01 par 0,01, j’obtiens ce qui suit:

Ouais, je je suis plutôt content de ça.