Cabestan! Une machinerie vieille de 6 siècles. Des milliers d’hommes robustes l’utilisaient pour soulever des cargaisons pour gagner leur vie, ou pour parcourir la mer sauvage, ou tout simplement pour la retourner sans raison évidente, mais pour construire un corps qui rendrait même Hercule jaloux.
Le 20ème siècle est arrivé, et l’humanité utilise toujours des cabestans mais d’une manière moins virile. Ils sont alimentés électriquement, hydrauliquement ou même via des moteurs à combustion interne. Les cabestans sont également utilisés dans nos bandes bien-aimées. Oui ceux avec de la musique sur également connus sous le nom de cassettes. Ceux que vous mixiez pour donner à la fille que vous aimiez le jour de la Saint-Valentin, ou ceux qu’un petit gars plein de zits vous a donnés le jour de la Saint-Valentin au lycée.
Comment cela a-t-il fonctionné? Le cabestan servait à déplacer la bande d’enregistrement à travers le mécanisme d’un magnétophone. Le ruban est enfilé entre le cabestan et une ou plusieurs roues recouvertes de caoutchouc, appelées rouleaux pinceurs, qui s’appuient contre le cabestan, assurant ainsi le frottement nécessaire au cabestan pour tirer le ruban. Le cabestan est toujours placé en aval (dans le sens du mouvement de la bande) des têtes de bande. Pour maintenir la tension requise contre les têtes de bande et toute autre partie du transport de bande, une petite quantité de traînée est placée sur la bobine d’alimentation. Les cabestans de magnétophone ont une fonction similaire aux cabestans nautiques, qui n’ont cependant pas de rouleaux pinceurs, la ligne étant simplement enroulée autour d’eux.
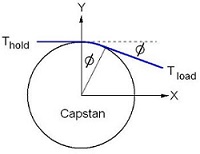Il existe également une équation de cabestan. L’équation de cabestan ou équation de frottement de courroie, également connue sous le nom de formule d’Eytelwein, relie la force de maintien à la force de charge si une ligne flexible est enroulée autour d’un cylindre (une borne, un treuil ou un cabestan). En raison de l’interaction des forces de frottement et de la tension, la tension sur une ligne enroulée autour d’un cabestan peut être différente de chaque côté du cabestan. Une petite force de maintien exercée d’un côté peut supporter une force de chargement beaucoup plus importante de l’autre côté ; c’est le principe selon lequel fonctionne un dispositif de type cabestan.
L’équation est celle de gauche et la charge est la tension appliquée sur la ligne (N), la force résultante exercée de l’autre côté du cabestan (N), μ le coefficient de frottement entre la corde et les matériaux du cabestan (sans dimension) et φ est l’angle total balayé par toutes les spires de la corde (radians).
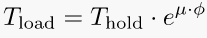
Allez-y, vérifiez cette équation et recherchez tout ce que vous voulez résoudre. Vous trouverez de l’aide dans notre vidéo fxSolver.
N’oubliez pas de suivre ou d’interagir avec nous dans nos pages de médias sociaux. Vous trouverez des liens ci-dessous.
