Lass uns das machen. Ich werde den Ausdruck für den Massenschwerpunkt für ein rechtwinkliges Dreieck ableiten. Warum?

Sehen Sie, wir werden Spaß haben. Ich habe bereits ein Yoda-Mem aufgenommen. Was könnte schief gehen?
Hier ist das Dreieck.

sieht aus wie ein normales blaues Dreieck. Stimmt’s? Aber angenommen, dies ist ein dünnes Blech mit einer Masse von M. Wie würden Sie die Position des Massenschwerpunkts finden? Beginnen wir mit der grundlegenden Definition des Massenschwerpunkts.

Dies ist im Wesentlichen ein gewichteter Durchschnitt. OK, es IST ein gewichteter Durchschnitt. Wenn Sie das Objekt jedoch in eine Reihe winziger Teile zerlegen, multiplizieren Sie die Vektorposition jeder Masse und ihrer winzigen Masse. Dann addieren Sie dann alles und dividieren durch die Gesamtmasse. Das ist das Zentrum der Masse. Hier ist ein anderes Bild.

atürlich haben wir in diesem Fall nicht viele Stücke. Wir haben eine kontinuierliche Masse. Das heißt, wir können stattdessen die Summe in ein Integral umwandeln. Anstatt mich gleichzeitig mit der x- und der y-Richtung zu befassen, werde ich nur den y-Massenschwerpunkt betrachten.
Ich beginne damit, dieses Dreieck in eine Reihe horizontaler Rechtecke zu zerlegen. Hier ist eines dieser Rechtecke.

Also, Ich kann diese dünnen Rechtecke verwenden, um den Massenmittelpunkt zu finden. Ich muss nur die Position jedes Rechtecks und die Masse jedes Rechtecks multiplizieren. Die Position ist ziemlich einfach, es ist „y“. Die Masse ist etwas kniffliger. Beachten Sie auch, dass Rechtecke, die sich im Dreieck nach oben bewegen, mit einer geringeren Masse kleiner sind.
Die Fläche dieses kleinen Rechtecks sollte proportional zu seiner Fläche sein. Lassen Sie mich die Flächendichte für das gesamte Dreieck wie folgt definieren:

Das bedeutet, dass die Masse des winzigen Rechtecks der winzige Wert (dm) ist, der von seiner Fläche abhängt.
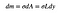
Schließlich muss ich L in Bezug auf y. Ich werde das tun, indem ich zuerst einen Ausdruck in Bezug auf x bekomme. Ich kann die linke Seite des Rechtecks „x“ und die rechte Seite „s“ nennen. Dies bedeutet, dass:

Aber die linke Seite dieses Dreiecks kann als eine Linie mit der Gleichung beschrieben werden:
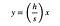
Wobei (h / s) die Steigung ist. Ich kann diese Gleichung für x lösen und in den Ausdruck für L ersetzen.

Wie wäre es mit einem schnellen Reality Check. Lassen Sie uns nur sicherstellen, dass die Dinge funktionieren, bevor wir zu weit kommen. Was ist, wenn wir y = h lassen? Das sollte am oberen Rand des Dreiecks mit einer Rechtecklänge von Null sein. Jep. Das funktioniert. Was ist mit y = 0? Das Rechteck sollte eine Länge von s haben.
Jetzt muss ich nur noch das ganze Zeug zusammenfügen. Dies ist die Masse dieser Scheibe eines Rechtecks.

Das „s“ bricht FTW für den Sieg).
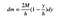
Das ist gut genug für jetzt. Der nächste Schritt besteht darin, einen Ausdruck für den y-Massenschwerpunkt zu schreiben. Da ich die Breite dieses Stücks auf Null gehen lasse, erhalte ich ein Integral anstelle einer Summe.

Ich kann das integrieren, aber es ist einfacher, wenn ich es in zwei Teile teile. Nur ein bisschen Algebra gibt mir:

Jetzt kann ich integrieren. Hier ist, was ich bekomme.

Bewertung an den Grenzen (was einfach ist, da die untere Grenze Null ist):

Boom. Das ist der y-Massenschwerpunkt. Es hat sogar Entfernungseinheiten (was es sollte). Beachten Sie auch, dass der y-Massenschwerpunkt nicht von der Länge des Dreiecks in x-Richtung abhängt (der Parameter s). Das ist cool. Es bedeutet auch, dass wir den x-Massenschwerpunkt leicht finden können. Alles, was ich tun muss, ist, dasselbe Dreieck in vertikale Rechtecke zu unterteilen.

Um die Mathematik in x-Richtung gleich zu machen, müsste ich den Ursprung in die andere Ecke des Dreiecks verschieben. Dies bedeutet, dass der x-Massenschwerpunkt (1/3) s von der rechten Seite entfernt ist. Dies ergibt einen Gesamtschwerpunkt von:

Cool.
Numerische Berechnung des Massenschwerpunkts
Oh, du dachtest, ich wäre fertig? Ich bin noch nicht fertig. Wie wäre es damit – eine numerische Berechnung des Massenschwerpunkts? Ja, es wird Spaß machen. Hier ist mein Plan.
- Wählen Sie die tatsächlichen Abmessungen eines Dreiecks aus. Ich kann keine numerische Berechnung mit Variablen durchführen. Ich brauche Zahlen. Ich werde s = 4, h = 1 verwenden. Ja, es sollte Einheiten geben, aber es wird keine Rolle spielen. OK, die Flächendichte ist 1 (es sollte klar sein, dass das auch keine Rolle spielt).
- Wählen Sie eine kleine Schrittweite. Angenommen, ich habe winzige Blöcke mit einer Größe von 0,01 x 0,01. Finden Sie die Vektorposition dieses Blocks und seine Masse (alle Blöcke haben die gleiche Masse).
- Verwenden Sie die Summenformelversion des Massenschwerpunkts.
- Bewegen Sie den Block entlang, bis alle Teile des Dreiecks bedeckt sind.
Machen wir das. OK, es gibt eine kleine Schwierigkeit. Ich muss eine Schleife in einer Schleife machen. Die innere Schleife addiert Quadrate entlang der x-Achse von der linken Neigung zu x = h. Die äußere Schleife bewegt diese horizontalen Zeilen von 0 nach h.
Hier ist der Hauptteil des Codes (vollständiger Code hier ):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
Mit einer Stückgröße von 0,01 mal 0,01 erhalte ich Folgendes:

Ja, damit bin ich ziemlich zufrieden.
