Cesaro Summierbarkeit

Es gibt mehr als eine Möglichkeit, eine unendliche Reihe zu summieren. Mit Cesàro Summation können Sie die Summe von Reihen berechnen, die keine Summe im klassischen Sinne haben.

Angenommen, wir haben eine unendliche Reihe

$a_0 + a_1 + a_2 + \cdots$

Die n-te Teilsumme der Reihe ist gegeben durch

$S_n = \sum_{i=0}^n a_i$

Die klassische Summe der Reihe, wenn sie existiert, ist definiert als die Grenze ihrer Teilsummen. Das heißt,

$\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\to\infty} \sum_{i=0}^n a_i$

Die Cesàro-Summierung verfolgt einen anderen Ansatz. Anstatt die Grenze der Teilsummen zu nehmen, nimmt es die Grenze der Mittelwerte der Teilsummen. Um genau zu sein, definieren Sie

$C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}$

und definieren Sie die Cesàro-Summation als die Grenze des Cn, wenn n gegen unendlich geht. Wenn eine Reihe eine Summe im klassischen Sinne hat, hat sie auch eine Summe im Cesàro-Sinne, und die Grenzen sind die gleichen. Aber einige Serien haben eine Cesàro-Summe, die keine klassische Summe hat. Oder vielleicht gibt es beide Grenzen, aber die Zwischenschritte der Cesàro-Summierung verhalten sich besser, wie wir in einem Beispiel unten sehen werden.

Wenn Sie das Cn in Bezug auf die ursprünglichen an ausdrücken, erhalten Sie

$C_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i$

Mit anderen Worten, die n-te Cesàro-Teilsumme ist eine Neugewichtung der klassischen Teilsummen, wobei sich die Gewichtungen als Funktion von n ändern. Beachten Sie, dass für das feste i der Bruch die Multiplikation von ai geht zu 1, wenn n zunimmt.

Fejér-Summation und Gibbs-Phänomen

Die Fejér-Summation ist eine Cesàro-Summation, die auf Fourier-Reihen angewendet wird. Die (gewöhnlichen) Teilsummen einer Fourier-Reihe ergeben die beste Annäherung an eine Funktion, gemessen nach der Norm der kleinsten Quadrate. Aber die Cesàro-Teilsummen können qualitativ eher der angenäherten Funktion ähneln. Wir demonstrieren dies unten mit einer Rechteckwelle.

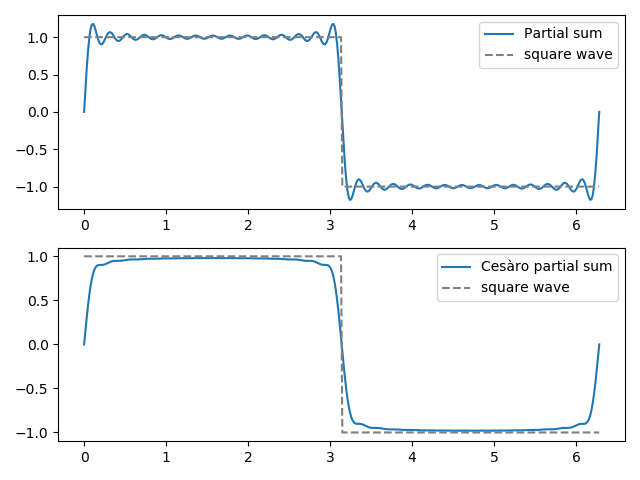
Die 30. gewöhnliche Teilsumme zeigt die Anfänge des Gibbs-Phänomens, die „Fledermausohren“ oben auf der Rechteckwelle und ihr Spiegelbild unten. Die 30. Cesàro-Teilsumme ist glatter und eliminiert Gibbs-Phänomene in der Nähe der Diskontinuität in der Rechteckwelle.

KGSAU

Cesàro Summierung

Fejér-Summation und Gibbs-Phänomen

Weitere Beiträge zur Fourier-Reihe

Schreibe einen Kommentar Antworten abbrechen