Wie erinnerst du dich an die Stelle auf einer einsamen Insel, an der du deinen Schatz vergraben hast? Sie wählen ein Wahrzeichen, sagen wir eine Palme, und messen, wie viele Schritte Nord / Süd und wie viele Schritte Ost / West Sie von diesem Wahrzeichen aus gehen müssen, um zum Schatz zu gelangen. Es ist eine einfache Idee, aber überraschenderweise dauerte es Jahrhunderte, bis Mathematiker ihr volles Potenzial auf ihrem eigenen Gebiet entfalten konnten. Als sie es schließlich taten, revolutionierte es die Mathematik, indem es zwei Bereiche zusammenbrachte, die auf den ersten Blick wenig miteinander zu tun haben: Algebra und Geometrie.
Wenn wir anfangen, Geometrie zu lernen, denken wir normalerweise an einfache Formen wie Linien, Dreiecke und Kreise in der zweidimensionalen Ebene. Sie können diese und kompliziertere Formen mit einem Lineal, einem Kompass und einem Winkelmesser konstruieren. Die alten Griechen waren Meister dieser Art von Geometrie: mit nur Kompassen und einer geraden Kante (einem nicht markierten Lineal) konnten sie eine Reihe von Formen konstruieren und sogar mathematische Ergebnisse wie den Satz des Pythagoras mit diesen einfachen Werkzeugen beweisen.
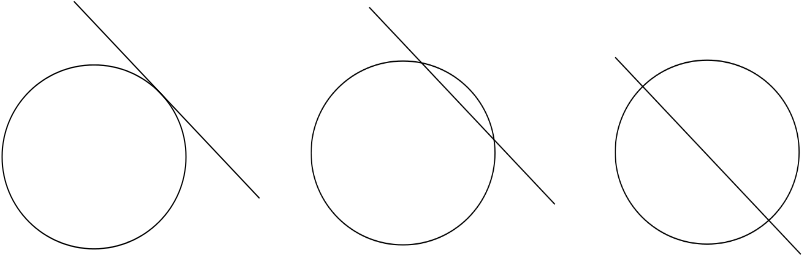
Es gibt jedoch bestimmte Dinge, die Sie mit diesen grundlegenden Methoden nicht tun können. Zwei Formen, sagen wir eine Linie und ein Kreis, können sich schneiden oder nicht, und sie können sich auf unterschiedliche Weise schneiden: Vielleicht berührt die Linie nur den Kreis, vielleicht rasiert sie einen kleinen Bogen davon oder vielleicht schneidet sie ihn in zwei Hälften. Um diese Informationen aufzuzeichnen, benötigen Sie eine Möglichkeit, die Positionen der Formen zu beschreiben.
Hier kommt die Idee der Schatzinsel ins Spiel. Es zeigt, was das kartesische Koordinatensystem genannt wird. Wählen Sie einen Punkt in der Ebene, den Ursprung, und zeichnen Sie zwei senkrechte Achsen, eine horizontale und eine vertikale. Jeder Punkt in der Ebene kann vom Ursprung aus erreicht werden, indem eine bestimmte Strecke \ (x \) entlang der horizontalen Achse und eine bestimmte Strecke \ (y \) entlang der vertikalen Achse zurückgelegt wird. Die Zahlen \((x,y)\) sind die Koordinaten des Punktes. Der Ursprung selbst hat Koordinaten \((0,0)\). Der Teil der horizontalen Achse (auch \(x\)-Achse genannt), der links vom Ursprung liegt, und der Teil der vertikalen Achse (die \(y\)-Achse) unterhalb des Ursprungs werden durch negative Zahlen beschrieben.Die kartesischen Koordinaten sind nach dem französischen Philosophen und Mathematiker René Descartes aus dem 17.Jahrhundert benannt. Es gibt eine (wahrscheinlich unwahre) Geschichte, dass Descartes diese Koordinaten erfand, während er im Bett lag und eine Fliege an der Decke beobachtete und sich fragte, wie er ihren Standort beschreiben sollte. Descartes ‚Vorliebe, bis mittags im Bett zu liegen, könnte tatsächlich die Ursache für seinen Tod gewesen sein, der 1650 in Stockholm stattfand. Descartes war in Schweden, um als Mathematiklehrer für Königin Christina zu fungieren, die es leider vorzog, früh am Morgen zu arbeiten. Berichten zufolge waren es diese frühen Morgenstunden und die skandinavischen Temperaturen, die die Lungenentzündung verursachten, die ihn schließlich tötete. Andere haben vorgeschlagen, dass er von einem katholischen Priester vergiftet wurde, der sich Sorgen um Descartes ‚radikale Theologie machte.In jedem Fall ist das kartesische Koordinatensystem eines der wichtigsten Vermächtnisse von Descartes (obwohl er nicht der einzige war, der die Idee hatte). Es erlaubt uns, geometrische Probleme mit Algebra zu beantworten und algebraische Zusammenhänge zu visualisieren, die sonst ziemlich abstrakt bleiben würden. Nehmen wir zum Beispiel die Gleichung \ Wir können den Graphen dieser Funktion in einem kartesischen Koordinatensystem zeichnen, indem wir alle Punkte zeichnen, deren Koordinaten die Form \((x,2x-1)\): punkte wie \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\ frac{1}{2}, -2)\), und \((1.73, 2.46)\). In diesem Fall ist der Graph eine gerade Linie, die am Punkt \((0,-1)\) auf die \(y\) -Achse trifft und eine Steigung von \(2\) hat.
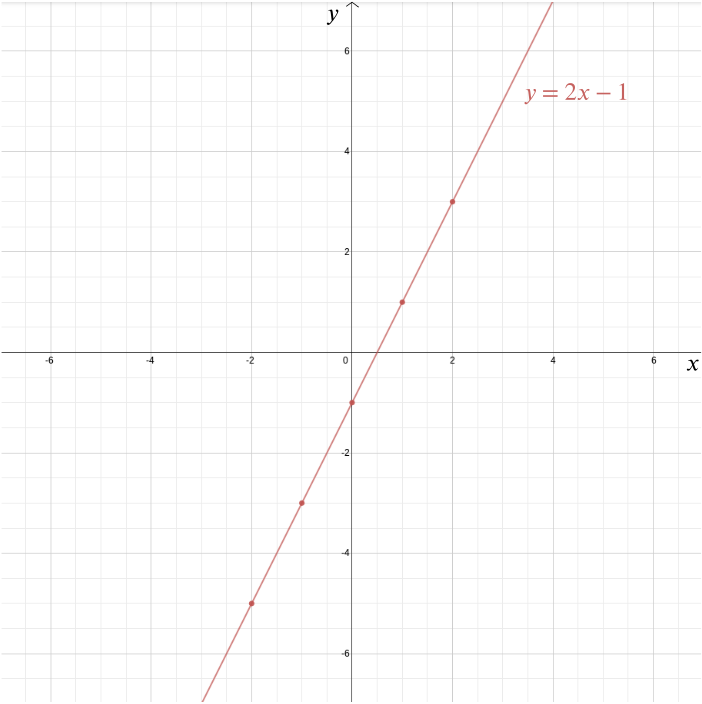
Allgemeiner ist jede Gerade durch eine Gleichung der Form \gegeben, wobei \(m\) die Steigung der Linie angibt und \((0,b)\) der Punkt ist, an dem sie die \(y\)-Achse kreuzt. Eine vertikale Linie, die die \(y\)-Achse nicht kreuzt, ist durch eine Gleichung der Form \(x=c\) gegeben. In diesem Fall ist \((c,0)\) der Punkt, an dem es die \(x\)-Achse kreuzt.
Was ist mit einem Kreis? Ein Kreis besteht aus all jenen Punkten, die in gleichem Abstand \(r\) von einem gegebenen Punkt \(m\) liegen. Angenommen, \(m\) ist der Punkt \((0,0)\). Aus dem Satz des Pythagoras wissen wir, dass, wenn ein Punkt \((x, y)\) in der Entfernung \(r\) von \((0,0)\) liegt, \
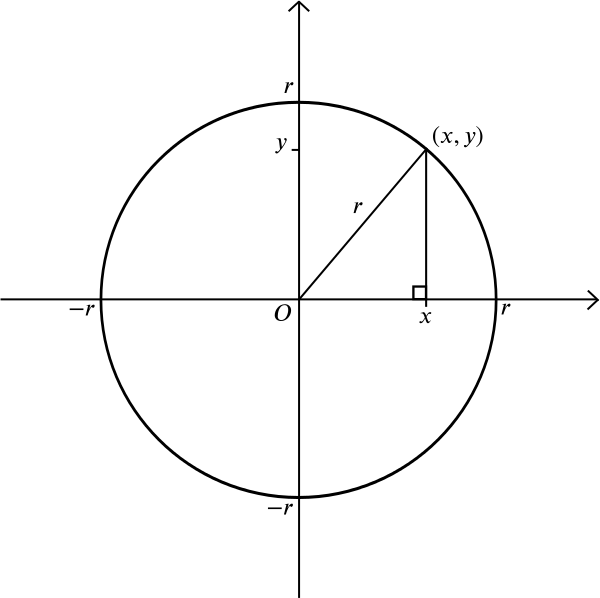
Dies ist also die Gleichung eines Kreises mit dem Radius \(r\), der auf den Ursprung zentriert ist. Sie können selbst herausfinden, dass ein Kreis mit dem Radius \(r\), der auf den Punkt \((a, b)\) zentriert ist, die Gleichung \ hat, aber hier ist eine kompliziertere Frage: welche Form erhalten Sie, wenn Sie alle Punkte betrachten, die in gleichem Abstand von einem bestimmten Punkt und einer bestimmten Linie liegen? Ohne ein Koordinatensystem können Sie den Punkt und die Linie zeichnen und mit Ihrem Lineal oder Zirkel experimentieren. Sie könnten ein paar Punkte zeichnen, die in gleichem Abstand von beiden liegen, und sehen, ob Sie die Gesamtform erraten können.
Bewaffnet mit einem Koordinatensystem wird die Antwort jedoch viel einfacher und präziser. Angenommen, der angegebene Punkt befindet sich im Abstand \ (1\) von der angegebenen Linie. Platzieren wir den gegebenen Punkt am Ursprung und die gegebene Linie so, dass sie horizontal ist, gegeben durch die Gleichung \ Nach dem Satz des Pythagoras ist der Abstand eines beliebigen Punktes \((x,y)\) von \((0,0)\) \(\sqrt{x^2 + y^2}\). Der Abstand von einem Punkt \((x,y)\) zur Linie \(y = -1\) ist \(|y+1|\) (wir verwenden hier den absoluten Wert, da die \(y\) -Koordinate negativ sein kann). Wenn diese beiden gleich sind, ergibt \ Quadrieren beider Seiten \ Neuordnen \ Also jeder Punkt in gleichem Abstand vom Punkt \((0,0)\) und die Linie \(y=-1\) hat Koordinaten \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Sie können selbst überprüfen, ob auch das Gegenteil der Fall ist: Jeder Punkt mit diesen Koordinaten liegt in gleichem Abstand vom Punkt \((0,0)\) und der Linie \(y= -1\).
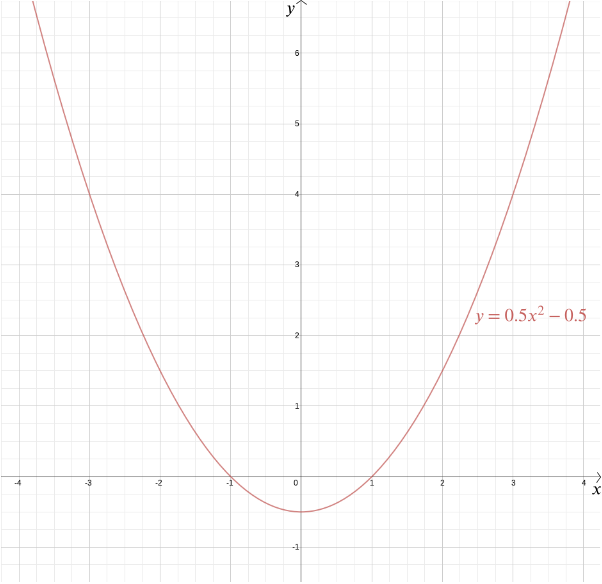
Wir können den Graphen dieser Funktion zeichnen, um die erforderliche Form zu sehen, die sich als Parabel herausstellt. Tatsächlich gibt uns jede quadratische Funktion \ für \ (a\), \ (b \) und \ (c \) Konstanten eine Parabel. Diese vertraute Form, die in so vielen subtilen Variationen auftreten kann — lang und dünn oder gedrungen und flach – wird von diesem praktischen algebraischen Ausdruck erfasst. Die Tatsache, dass heute die Begriffe „quadratische Funktion“ und „Parabel“ fast als synonym gelten, unterstreicht, wie erfolgreich Descartes ‚Idee war. Im Allgemeinen ergibt jede algebraische Beziehung zwischen zwei Variablen \ (x \) und \ (y \) eine Kurve, die wir mit kartesischen Koordinaten zeichnen können.
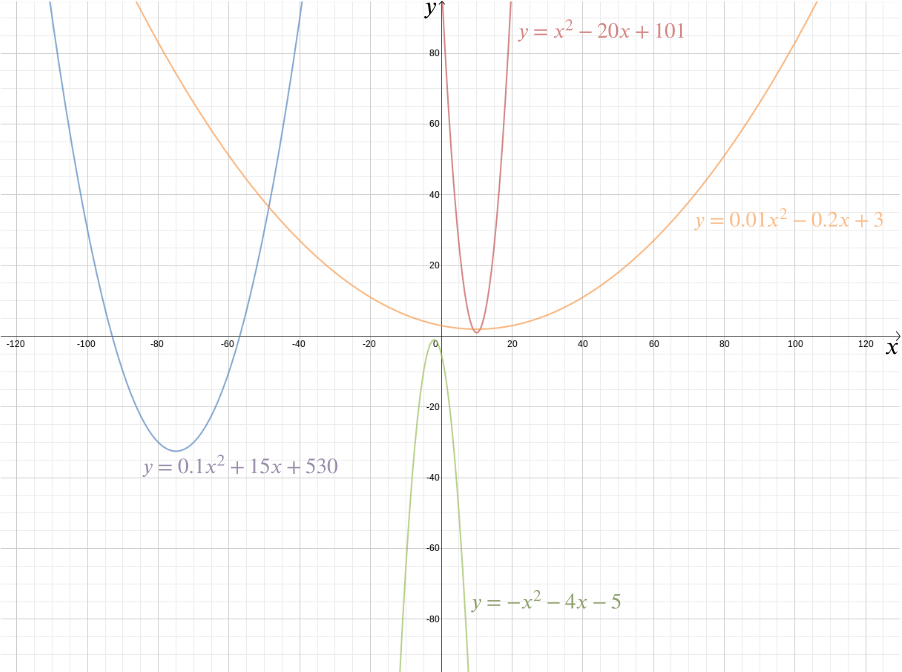
Die algebraische Darstellung erleichtert die Beantwortung einer ganzen Reihe geometrischer Fragen. Um die Schnittpunkte der durch \ und die Parabel \(y = \frac{x^2}{2} – \frac{1}{2}\) gegebenen Linie zu berechnen, beachten wir einfach, dass die \(y\) Koordinate eines beliebigen Punktes \((x,y)\), der auf beiden liegt, beide Gleichungen erfüllen muss, so dass \ Dies ergibt \ Lösen der quadratischen Gleichung erhalten wir \ und \ so sind die Schnittpunkte bei \
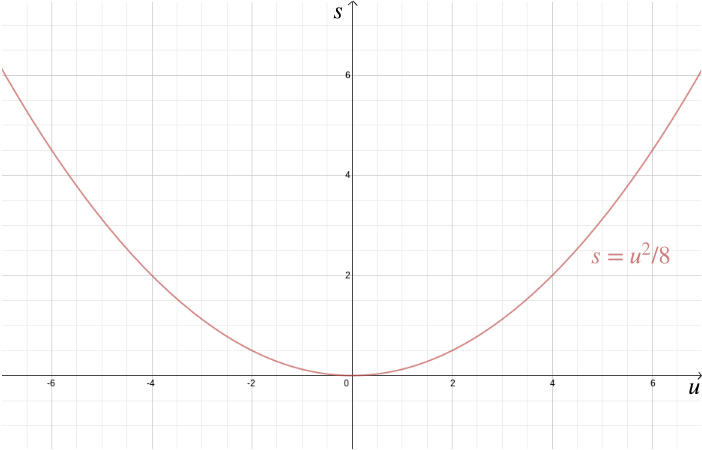
Neben der Lösung geometrischer Probleme helfen kartesische Koordinaten auch, algebraische Beziehungen zu visualisieren. Angenommen, ein Auto fährt mit der Geschwindigkeit \(u \) und der Fahrer bremst, was zu einer konstanten Verzögerung von beispielsweise \(-4 \) Metern / Sekunden \ (^ 2 \) führt. Der Bremsweg \(s\) – der Abstand, den das Auto zurücklegt, bevor es zum Stillstand kommt – ist durch die algebraische Beziehung gegeben \ Das Zeichnen mit kartesischen Koordinaten zeigt, wie wichtig es ist, in städtischen Gebieten langsamer zu fahren, da der Bremsweg mit \(u\) schnell zunimmt.
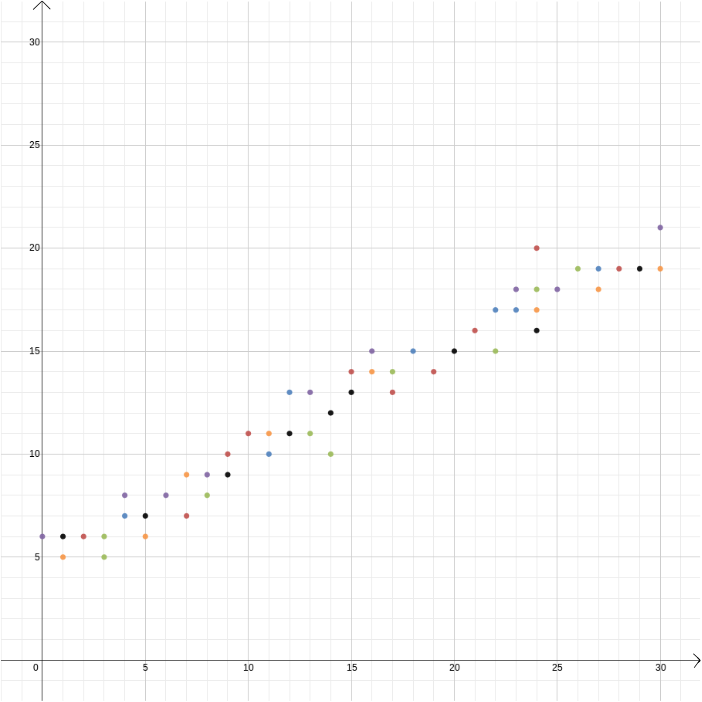
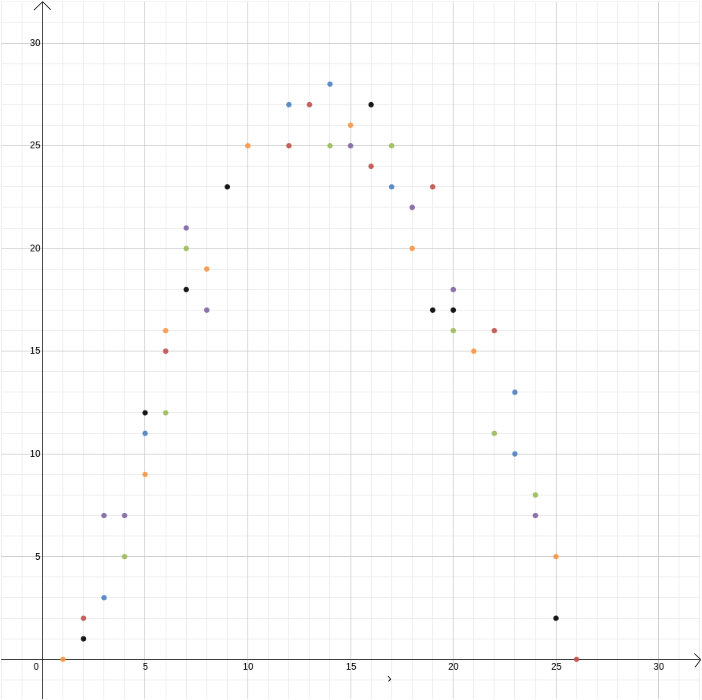
In diesem Beispiel kannten wir die Beziehung zwischen zwei Variablen, da sie aus den Gesetzen der Physik abgeleitet werden kann. Kartesische Koordinaten sind jedoch auch nützlich, wenn Sie den Verdacht haben, dass zwei Variablen verwandt sind, aber nicht wissen, wie. Angenommen, wir glauben, dass es eine Beziehung zwischen dem Gewinn eines Eisverkäufers und der Außentemperatur gibt. Um herauszufinden, wie diese Beziehung aussehen könnte, können wir Temperatur und Gewinn beispielsweise im Laufe eines Jahres messen und die Werte gegeneinander darstellen, wobei die Temperatur auf der \ (x \) -Achse und der Gewinn auf der \ (y \) -Achse aufgezeichnet werden. Wir können dann sehen, ob wir ein Muster erkennen können. Im ersten Diagramm unten können wir vermuten, dass die Beziehung linear ist, und wir können versuchen, die gerade Linie \ zu finden, die am besten zu unseren Daten passt (es gibt Methoden, um diese beste Anpassung zu finden). Im zweiten Diagramm unten können wir vermuten, dass die Beziehung quadratisch ist, und wir können erneut versuchen, die Funktion \ zu finden, die am besten zu den Daten passt.
Kartesische Koordinaten spielten in der zweiten Hälfte des 17. Kalkül ermöglicht es, Attribute von Kurven wie ihre Steigung an einem bestimmten Punkt oder die Fläche der Region, die zwischen einer Kurve und der \ (x \) -Achse liegt, zu berechnen. Diese können auch physische Interpretationen haben. Wenn wir beispielsweise die Entfernung, die ein Auto zurücklegt, gegen die Zeit, die es zurückgelegt hat, darstellen, stellt die Steigung der resultierenden Kurve zu einem bestimmten Zeitpunkt — die Änderungsrate der Entfernung in Bezug auf die Zeit — die Geschwindigkeit dar, mit der das Auto in diesem Moment gefahren ist in der Zeit: Es ist die Ableitung der Funktion, die uns Entfernung in Bezug auf Zeit gibt. Siehe auch Warum sind Farbverläufe in der realen Welt wichtig?.
Wir können auch eine Dimension nach oben gehen, indem wir eine dritte Achse senkrecht zu den ersten beiden betrachten, die Sie sich vorstellen können, wie Sie aus Ihrem Blatt Papier kommen und auf Sie zeigen. Mit einem solchen dreidimensionalen System können Sie nun dreidimensionale Objekte darstellen und visualisieren, wie eine dritte Variable \ (z\) von Ihren ersten beiden Variablen \ (x\) und \ (y\) abhängt.
Diese Beispiele sollen Ihnen einen Eindruck davon vermitteln, warum Koordinaten in allen Bereichen der Wissenschaft, von der Physik über die Astronomie und das Ingenieurwesen bis hin zur visuellen Industrie, um Computergrafiken und computergenerierte Bilder zu produzieren, die wir in Filmen und Spielen bewundern, so unverzichtbar geworden sind.
In der Mathematik selbst gipfelte die Verbindung zwischen Algebra und Geometrie in einem ganzen Gebiet namens algebraische Geometrie, das eine eigene Faszination besitzt. Das vielleicht berühmteste Ergebnis, das aus diesem Bereich hervorgegangen ist, ist Fermats letzter Satz, benannt nach einem Zeitgenossen von Descartes, Pierre de Fermat, der auch wesentlich zur Entwicklung des kartesischen Koordinatensystems beigetragen hat. Fermat dachte über eine Frage nach, die Geometrie mit Zahlentheorie verbindet. Nach dem Satz von Pythagoras, wenn \(a\), \(b\) und \(c\) sind die Seiten eines rechtwinkligen Dreiecks und \(c\) ist die Seite gegenüber dem rechten Winkel, dann \(a ^ 2 + b^ 2 = c ^ 2 \). Es gibt unendlich viele Tripel von ganzen Zahlen \(a\), \(b\) und \(c \), die diese Beziehung erfüllen; \((3,4,5)\) ist ein Beispiel.Nehmen wir nun an, wir ändern den Exponenten und betrachten Ausdrücke wie \ und \ und allgemeiner \, wobei \(n\) eine natürliche Zahl größer als \(2\) ist. Können wir immer noch positive ganze Zahlen \ (a \), \(b\) und \ (c \) finden, die die Gleichung erfüllen? Fermat vermutete, dass wir das nicht können, und er kritzelte so viel in den Rand seines Mathe-Lehrbuchs und sagte, er habe einen „wunderbaren Beweis“ für diese Tatsache, für den der Rand zu eng sei.
Dieses Kritzeln sollte Mathematiker über 350 Jahre lang verfolgen. Erst 1994 wurde vom Mathematiker Andrew Wiles endlich ein korrekter Beweis für dieses scheinbar harmlose Ergebnis angekündigt. Wiles hatte umfangreiche Verwendung der algebraischen Geometrie gemacht. Insbesondere hatte er Ergebnisse über die elliptischen Kurven verwendet, die durch Punkte in der Ebene beschrieben werden, deren Koordinaten \ Descartes ‚Betrachtung einer Fliege befriedigen hat einen langen Weg zurückgelegt!
