Låt oss göra detta. Jag kommer att härleda uttrycket för masscentrum för en rätt triangel. Varför?

se, vi kommer att ha kul. Jag har redan inkluderat en Yoda meme. Vad kan gå fel?

här är triangeln.

åh, ser ut som en vanlig blå triangel. Eller hur? Men antar att detta är en tunn metallplåt med en massa M. hur skulle du hitta platsen för massans centrum? Låt oss börja med den grundläggande definitionen av masscentrum.

detta är i huvudsak ett vägt genomsnitt. OK, det är ett vägt genomsnitt. Men om du bryter objektet i en massa små bitar, multiplicerar du vektorpositionen för varje massa och dess lilla massa. Sedan lägger du till allt och delar upp med den totala massan. Det är massans centrum. Här är en annan bild.

naturligtvis i det här fallet har vi inte en massa bitar. Vi har en kontinuerlig massa. Det betyder att vi istället kan göra summan till en integral. I stället för att hantera både x-och y-riktningarna samtidigt, kommer jag bara att överväga y-mitten av massan.

Jag börjar med att bryta denna triangel i en massa horisontella rektanglar. Här är en av dessa rektanglar.

så, jag kan använda dessa mager rektanglar för att hitta massans centrum. Jag behöver bara multiplicera positionen för varje rektangel och massan för varje rektangel. Positionen är ganska enkel, det är ”y”. Massan är lite mer knepig. Observera också att för rektanglar som rör sig upp i triangeln är de mindre med mindre massa.

området för denna lilla rektangel ska vara proportionell mot dess område. Låt mig definiera områdestätheten för hela triangeln som:

det betyder att massan av den lilla rektangeln kommer att vara det lilla värdet (dm) som beror på dess område.

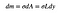
slutligen måste jag få l i termer av Y. jag kommer att göra det genom att först få ett uttryck i termer av X. Jag kan ringa vänster sida av rektangeln ” x ”och höger sida”s”. Detta betyder att:

men den vänstra sidan av den triangeln kan beskrivas som en linje med ekvationen:

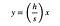
där (h / S) är lutningen. Jag kan lösa denna ekvation för x och ersätta uttrycket för L.

vad sägs om en snabb verklighetskontroll. Låt oss bara se till att saker fungerar innan vi kommer för långt. Vad händer om vi låter y = h? Det borde vara högst upp i triangeln med en rektangellängd på noll. Japp. Det fungerar. Vad sägs om y = 0? Rektangeln ska ha en längd av s. ser bra ut.

nu behöver jag bara sätta ihop alla dessa saker. Detta är massan av den skivan av en rektangel.

”s” avbryter FTW (för vinsten).

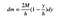
det är bra nog för nu. Nästa steg är att skriva ett uttryck för y-masscentret. Eftersom jag ska låta bredden på denna bit gå till noll, kommer jag att få en integral istället för en summa.

jag kan integrera detta, men det är lättare om jag bryter det i två delar. Bara lite algebra ger mig:

nu kan jag integrera. Här är vad jag får.

utvärdering vid gränserna (vilket är lätt eftersom den nedre gränsen är noll):

bom. Det är y-mitten av massan. Det har till och med enheter av avstånd (vilket det borde). Observera också att Y-mitten av massan inte beror på längden på triangeln i x-riktningen (parametern s). Det är coolt. Det betyder också att vi lätt kan hitta x-mitten av massan. Allt jag behöver göra är att bryta samma triangel i vertikala rektanglar.

för att göra matematiken densamma i x-riktningen, skulle jag behöva flytta ursprunget till det andra hörnet av triangeln. Detta betyder att X-mitten av massan är (1/3) s från höger sida. Detta ger ett totalt masscentrum av:

cool.

numerisk beräkning av masscentrum

Åh, trodde du att jag var klar? Jag är inte klar. Vad sägs om detta-en numerisk beräkning av masscentrum? Ja, det blir kul. Här är min plan.

• Välj faktiska dimensioner av en triangel. Jag kan inte göra en numerisk beräkning med variabler. Jag behöver siffror. Jag ska använda s = 4, h=1. Ja, det borde finnas enheter men det spelar ingen roll. OK, områdestätheten är 1 (Det borde vara klart att det inte spelar någon roll).
• välj en liten stegstorlek. Låt oss säga att jag har små block med storleken 0,01 med 0,01. Hitta vektorplatsen för detta block och dess massa (alla block har samma massa).
• använd sum formula-versionen av masscentrum.
• flytta blocket tills alla delar av triangeln är täckta.

Låt oss göra det här. OK, det finns en liten svårighet. Jag kommer att behöva göra en slinga inuti en slinga. Den inre slingan kommer att lägga upp rutor längs x-axeln från vänster lutning till x = h. den yttre slingan kommer att flytta dessa horisontella rader upp från 0 till h.

Här är huvuddelen av koden (full kod här):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

med en bitstorlek på 0,01 med 0,01 får jag följande:

ja, jag är ganska nöjd med det.