det finns mer än ett sätt att summera en oändlig serie. Med CES bisexro summation kan du beräkna summan av serier som inte har en summa i klassisk mening.

Antag att vi har en oändlig serie

den n: e delsumman av serien ges av

den klassiska summan av serien, om den existerar, definieras som gränsen för dess partiella summor. Det vill säga

cesubbiro summering tar ett annat tillvägagångssätt. I stället för att ta gränsen för delsummorna tar den gränsen för medelvärdena för delsummorna. För att vara specifik, definiera

och definiera ces Jacobro-summeringen för att vara gränsen för Cn när n går till oändlighet. Om en serie har en summa i klassisk mening, har den också en summa i cesubbiro-mening, och gränserna är desamma. Men vissa serier har en ces Bisexro summa som inte har en klassisk summa. Eller kanske båda gränserna finns, men mellanstegen i CES Usculiro summering är bättre uppförda, som vi ser i ett exempel nedan.

om du uttrycker Cn i termer av de ursprungliga an-termerna får du

med andra ord är nth ces Aucliro delsumma en omviktning av de klassiska delsummorna, med vikterna som ändras som en funktion av n. Observera att för fast i, fraktionen som multiplicerar ai går till 1 När n ökar.

fej Actuir summering och Gibbs fenomen

fej Actuir summering är ces Actuiro summering tillämpas på Fourier-serien. De (vanliga) delsummorna i en Fourier-serie ger den bästa approximationen till en funktion mätt med minsta kvadratnorm. Men de partiella summorna i Cesubbiro kan vara kvalitativt mer som den funktion som approximeras. Vi demonstrerar detta nedan med en kvadratvåg.

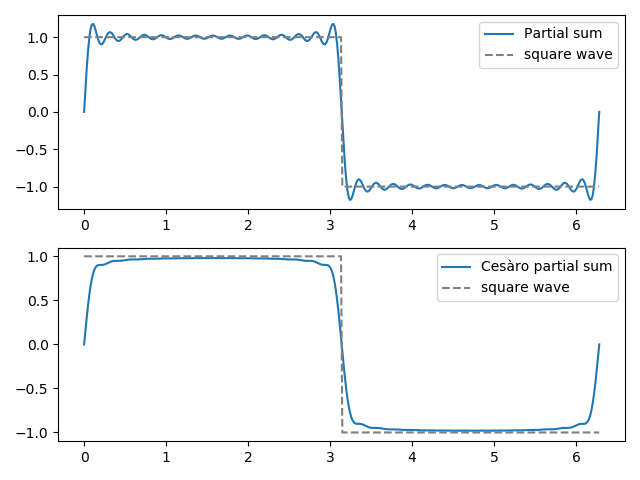
den 30: e vanliga delsumman visar början på Gibbs-fenomenet,” fladdermusöron ” högst upp på kvadratvågen och deras spegelbild längst ner. Den 30: e ces usci-delsumman är mjukare och eliminerar Gibbs-fenomen nära diskontinuiteten i kvadratvågen.

fler Fourier series-inlägg

• Fourier-Bessel-serien
• motprov till Dirichlet-principen
• klippta sinusvågor