hur kommer du ihåg platsen på en öde ö där du begravde din skatt? Du väljer ett landmärke, säger ett palmer och mäter hur många steg norr/söder och hur många steg Öst/Väst du måste gå från det landmärket för att komma till skatten. Det är en enkel ide men överraskande tog matematiker århundraden för att utveckla sin fulla potential inom sitt eget område. När de äntligen gjorde det revolutionerade det matematiken genom att sammanföra två områden som på framsidan av det har lite att göra med varandra: algebra och geometri.
När vi börjar lära oss geometri tänker vi vanligtvis på enkla former som linjer, trianglar och cirklar i det tvådimensionella Planet. Du kan konstruera dessa och mer komplicerade former med hjälp av en linjal, kompasser och gradskiva. De gamla grekerna var mästare på denna typ av geometri: med bara kompasser och en rak kant (en omärkt linjal) kunde de konstruera en rad former och de kunde till och med bevisa matematiska resultat, såsom Pythagoras sats, med hjälp av dessa enkla verktyg.
det finns dock vissa saker som du inte kan göra med dessa grundläggande metoder. Två former, säg en linje och en cirkel, kanske eller kanske inte korsar varandra, och de kan korsa på olika sätt: kanske berör linjen bara cirkeln, kanske rakar den en liten båge av den, eller kanske skär den den i hälften. För att registrera denna information behöver du ett sätt att beskriva placeringen av formerna.
det är här treasure island-tanken kommer till nytta. Det illustrerar vad som kallas det kartesiska koordinatsystemet. Välj en punkt i planet, kallad ursprunget, och dra två vinkelräta axlar genom den, en horisontell och en vertikal. Varje punkt i planet kan nås från ursprunget genom att resa ett visst avstånd \(x\) längs den horisontella axeln och ett visst avstånd \(y\) längs den vertikala axeln. Siffrorna \((x,y)\) är koordinaterna för punkten. Ursprunget i sig har koordinater \((0,0)\). Den del av den horisontella axeln (även kallad \(x\)-axeln) som ligger till vänster om ursprunget och den del av den vertikala axeln (\(y\)-axeln) under ursprunget beskrivs med negativa tal.
kartesiska koordinater är uppkallade efter den 17: e århundradet franska filosofen och matematikern ren Slovakia Descartes. Det finns en (förmodligen osann) historia att Descartes uppfann dessa koordinater medan de låg i sängen och tittade på en fluga i taket och undrade hur man beskriver sin plats. Descartes förkärlek för att ligga i sängen fram till middagstid kan faktiskt ha varit orsaken till hans bortgång, som inträffade i Stockholm 1650. Descartes var i Sverige för att fungera som mattehandledare till Drottning Christina, som Tyvärr föredrog att arbeta tidigt på morgonen. Enligt vissa rapporter var det dessa tidiga timmar och de skandinaviska temperaturerna som orsakade lunginflammation som så småningom dödade honom. Andra har föreslagit att han förgiftades av en katolsk präst som oroade sig för Descartes radikala teologi.
hur som helst är det kartesiska koordinatsystemet en av Descartes viktigaste arv (även om han inte var den enda personen som hade tanken). Det gör att vi kan svara på geometriska problem med algebra och visualisera algebraiska relationer som annars skulle förbli ganska abstrakta. Ta till exempel ekvationen \ vi kan plotta grafen för denna funktion i ett kartesiskt koordinatsystem genom att plotta alla punkter vars koordinater är av formen \((x, 2x-1)\): punkter som \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), och \((1.73, 2.46)\). I detta fall är grafen en rak linje som möter\(y\)-axeln vid punkten\ ((0,-1)\) och har en lutning på\(2\).
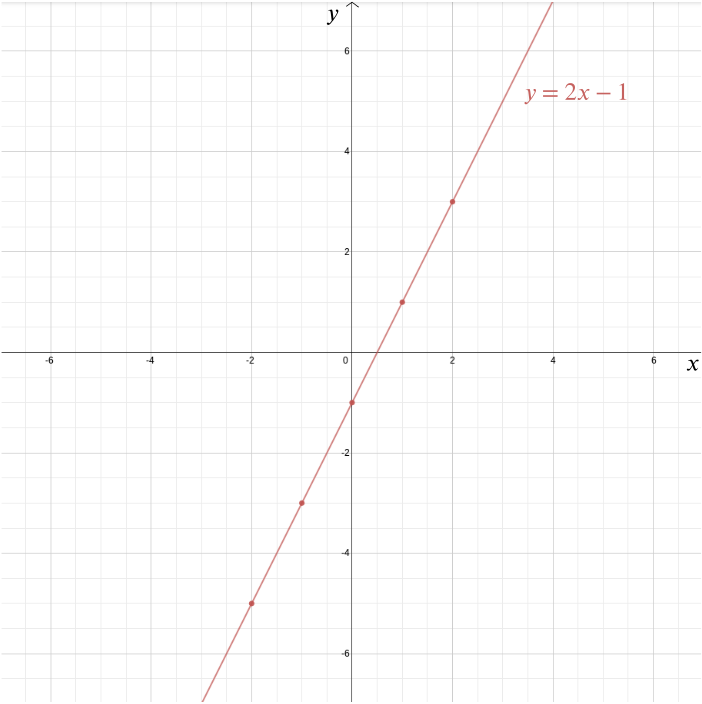
Mer Allmänt ges varje rak linje av en ekvation av formen \ där \(m\) ger dig linjens lutning och \((0,b)\) är den punkt där den korsar \(y\)-axeln. En vertikal linje som inte korsar\(y\)-axeln ges av en ekvation av formen\(x=c\). I detta fall är \((c,0)\) den punkt där den korsar \(x\)-axeln.
vad sägs om en cirkel? En cirkel består av alla de punkter som ligger på lika avstånd \(r\) från en given punkt \(m\). Låt oss anta att \(m\) är punkten \((0,0)\). Från Pythagoras sats vet vi att om en punkt \((x, y)\) ligger på avstånd \(r\) från \((0,0)\), då \
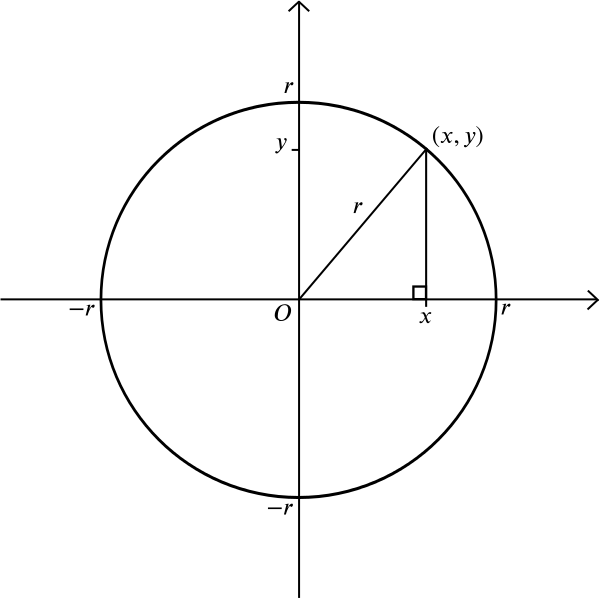
detta är därför ekvationen för en cirkel med radie \(r\) centrerad på ursprunget. Du kan själv räkna ut att en cirkel med radie \(r\) centrerad på punkten \((a,b)\) har ekvationen \ men här är en mer komplicerad fråga: vilken form får du när du tänker på alla punkter som ligger på samma avstånd från en given punkt och en given linje? Utan ett koordinatsystem kan du rita punkten och linjen och experimentera med din linjal eller kompasser. Du kan rita några punkter som ligger på lika avstånd från båda och se om du kan gissa den övergripande formen.
beväpnad med ett koordinatsystem blir svaret dock mycket enklare och mycket mer exakt. Antag att den givna punkten är på avstånd \(1\) från den angivna linjen. Låt oss placera den givna punkten vid ursprunget och den givna linjen så att den är horisontell, givet av ekvationen \ av Pythagoras sats avståndet för vilken punkt som helst \((x,y)\) från \((0,0)\) är \(\sqrt{x^2 + y^2}\). Avståndet från en punkt \((x,y)\) till linjen \(y = -1\) är \(|y+1|\) (Vi använder det absoluta värdet här eftersom \(y\)-koordinaten kan vara negativ). Om dessa två är lika, ger \ Squaring båda sidor \ Rearranging ger \ så någon punkt på lika avstånd från punkten \((0,0)\) och linjen \(y=-1\) har koordinater \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Du kan själv kontrollera att det omvända också är sant: varje punkt med dessa koordinater ligger på lika avstånd från punkten \((0,0)\) och linjen \(y=-1\).
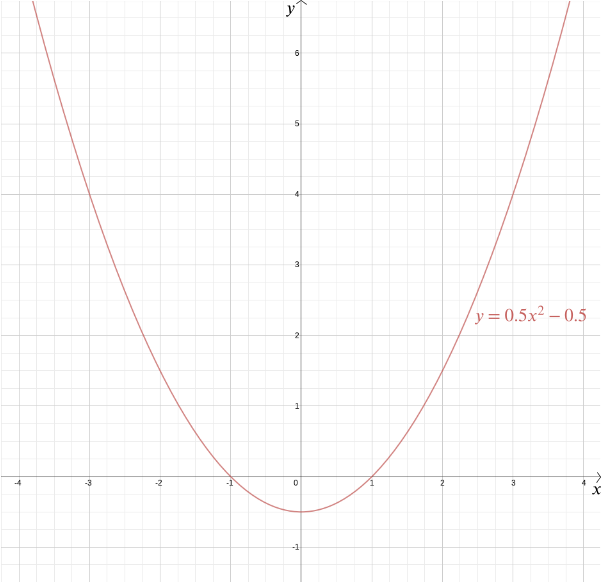
Vi kan plotta grafen för denna funktion för att se önskad form, som visar sig vara en parabola. Faktum är att varje kvadratisk funktion \ för \(a\), \(b\) och \(c\) konstanter ger oss en parabola. Denna välbekanta form, som kan komma i så många subtila variationer—lång och tunn eller squat och platt—fångas av detta praktiska algebraiska uttryck. Det faktum att termen ”kvadratisk funktion” och ”parabola” idag nästan anses vara synonymt belyser hur framgångsrik Descartes IDE har varit. Mer allmänt ger alla algebraiska förhållanden mellan två variabler \(x\) och \(y\) oss en kurva som vi kan plotta med kartesiska koordinater.
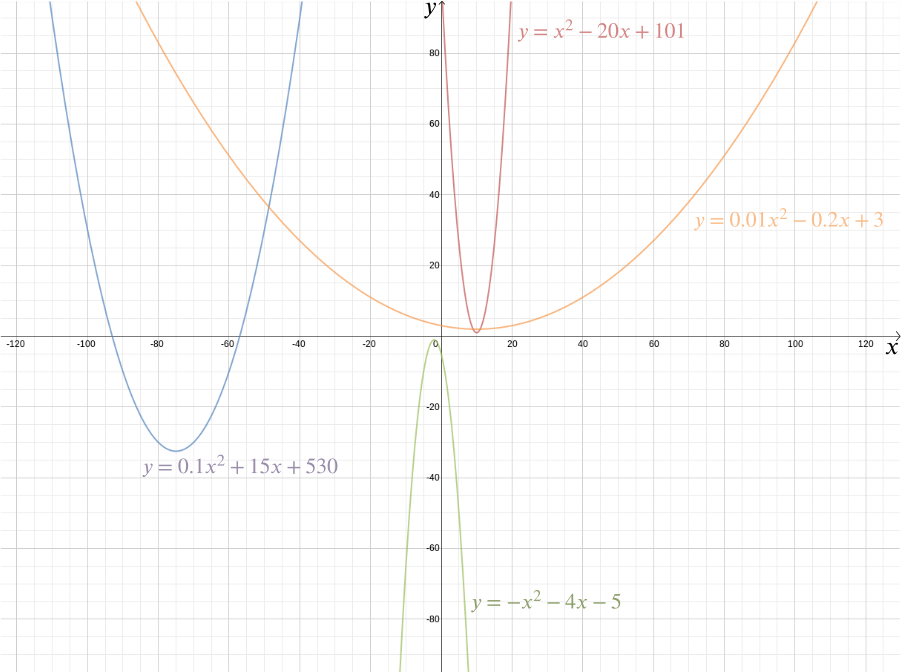
den algebraiska representationen gör det enkelt att svara på en hel rad geometriska frågor. För att räkna ut skärningspunkterna för linjen som ges av \ och parabolen \(y = \frac{x^2}{2} – \frac{1}{2}\) noterar vi helt enkelt att \(y\) koordinaten för vilken punkt som helst \((x, y)\) som ligger på båda måste uppfylla båda ekvationerna,så \ detta ger \ Lösa den kvadratiska ekvationen vi får \ och \ så skärningspunkterna är vid \
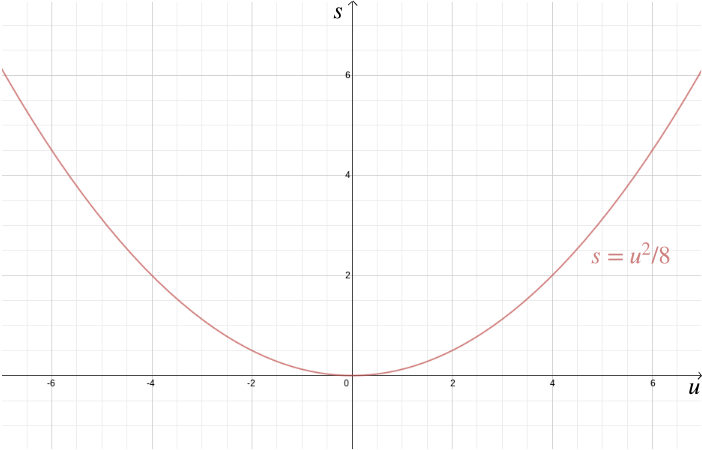
förutom att lösa geometriska problem, hjälper kartesiska koordinater också att visualisera algebraiska relationer. Anta till exempel att en bil kör i hastighet \(u\) och föraren bromsar, vilket resulterar i en konstant retardation av till exempel \(-4\) meter/sekunder\(^2\). Stoppavståndet \(s\)—avståndet som bilen täcker innan den stannar—ges av det algebraiska förhållandet \ Plotting detta med kartesiska koordinater ger hem hur viktigt det är att sakta ner i stadsområden, eftersom stoppavståndet ökar snabbt med \(u\).
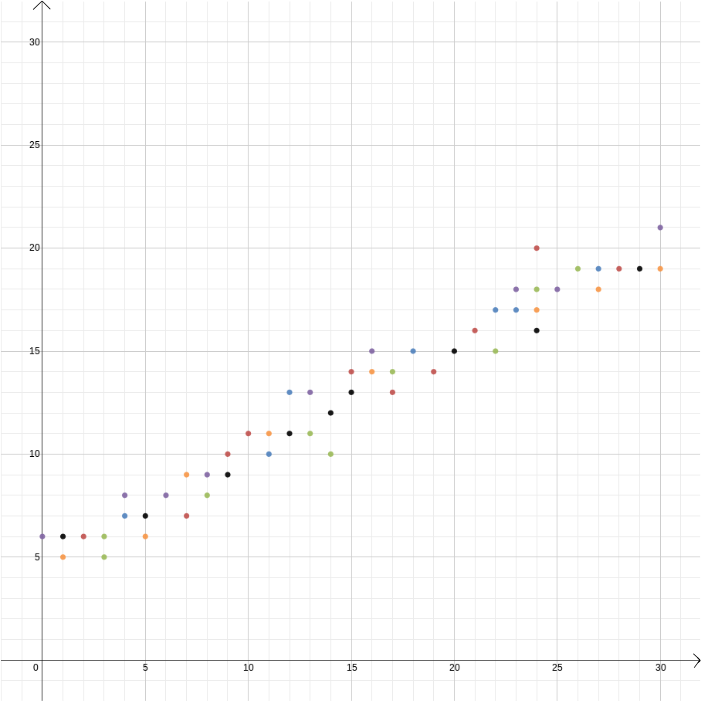
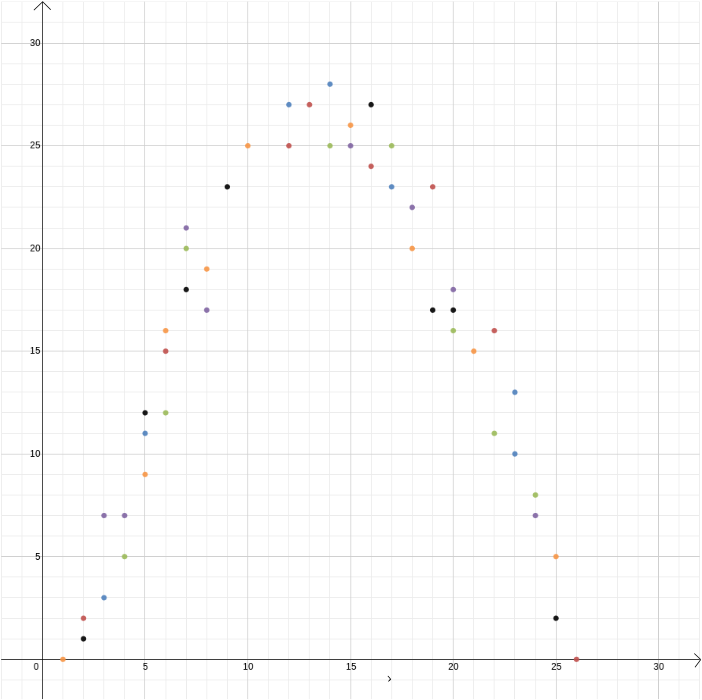
i det här exemplet visste vi förhållandet mellan två variabler eftersom det kan härledas från fysikens lagar. Men kartesiska koordinater är också användbara när du misstänker att två variabler är relaterade men du vet inte hur. Antag att vi tror att det finns ett samband mellan vinsten från en glassförsäljare och utetemperaturen. För att ta reda på vad det förhållandet kan vara, kan vi mäta temperatur och vinst över, säg, ett år och plotta värdena mot varandra, med temperatur inspelad på \(x\)-axeln och vinst på \(y\)-axeln. Vi kan sedan se om vi kan upptäcka ett mönster. I det första diagrammet nedan kan vi gissa att förhållandet är linjärt, och vi kan försöka hitta den raka linjen \ som bäst passar våra data (Det finns metoder för att hitta den bästa passformen). I det andra diagrammet nedan kan vi gissa att förhållandet är kvadratiskt och igen kan vi försöka hitta den funktion som bäst passar data.
kartesiska koordinater spelade en viktig roll i utvecklingen av kalkylen under andra hälften av 17-talet. Calculus gör det möjligt att utarbeta attribut av kurvor som deras lutning vid en given punkt eller området i regionen som ligger mellan en kurva och \(x\)-axeln. Dessa kan också ha fysiska tolkningar. Om vi till exempel plottar Avståndet en bil färdas mot den tid den har färdats, representerar lutningen på den resulterande kurvan vid en given tidpunkt—hastigheten för förändring av avstånd med avseende på tid—den hastighet med vilken bilen färdades i det ögonblicket: det är derivatet av funktionen som ger oss avstånd i termer av tid. Se också Varför är gradienter viktiga i den verkliga världen?.
Vi kan också gå upp en dimension genom att överväga en tredje axel vinkelrätt mot de två första, som du kan föreställa dig som kommer ut ur ditt pappersark och pekar på dig. Med hjälp av ett sådant tredimensionellt system kan du nu representera tredimensionella objekt och visualisera hur en tredje variabel \(z\) beror på dina första två, \(x\) och \(y\).
dessa exempel bör ge dig en känsla av varför koordinater har blivit så oumbärliga inom alla vetenskapsområden, från fysik till astronomi och teknik, och även i visuella industrier för att producera datorgrafik och datorgenererade bilder vi beundrar i filmer och spel.
i själva matematiken har kopplingen mellan algebra och geometri kulminerat i ett helt område som kallas algebraisk geometri, som har en egen fascination. Det kanske mest kända resultatet som har uppstått från detta område är Fermats sista sats, uppkallad efter en samtida av Descartes, Pierre de Fermat, som också bidrog väsentligt till utvecklingen av det kartesiska koordinatsystemet. Fermat övervägde en fråga som länkar geometri till talteori. Enligt Pythagoras sats, om \(a\), \(b\) och \(c\) är sidorna av en rätvinklig triangel och \(c\) är sidan motsatt rätt vinkel, då \(a^2 + b^2 = c^2\). Det finns oändligt många tripplar av heltal \(a\), \(b\) och \(c\) som uppfyller detta förhållande; \((3,4,5)\) är ett exempel.
antar nu att vi ändrar exponenten och överväger uttryck som \ och \ och mer generellt \ där \(n\) är ett naturligt tal större än \(2\). Kan vi fortfarande hitta positiva heltal \(a\), \(b\) och \(c\) som uppfyller ekvationen? Fermat misstänkte att vi inte kan och han klottrade så mycket i marginalen i sin matematiska textbok och sa att han hade ett ”fantastiskt bevis” för det faktum som marginalen var för smal för att innehålla.
att klottra var att hemsöka matematiker i över 350 år. Det var inte förrän 1994 att ett korrekt bevis på detta till synes oskyldiga resultat slutligen tillkännagavs av matematikern Andrew Wiles. Wiles hade gjort omfattande användning av algebraisk geometri. I synnerhet hade han använt resultat om de elliptiska kurvorna som beskrivs av punkter i planet vars koordinater uppfyller \ Descartes kontemplation av en fluga har kommit långt!
