Cesaro sumability

există mai multe modalități de a însuma o serie infinită. Cesextro însumare vă permite să calculați suma seriilor care nu au o sumă în sensul clasic.

Să presupunem că avem o serie infinită

$a_0 + a_1 + a_2 + \cdots$

A N-A sumă parțială a seriei este dată de

$S_n = \sum_{i=0}^n a_i$ p

suma clasică a seriei, dacă există, este definită ca fiind limita sumelor sale parțiale. Cu alte cuvinte,

$\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{N\to\infty} \sum_{i=0}^n A_i$

ces Unqustro însumare are o abordare diferită. În loc să ia limita sumelor parțiale, este nevoie de limita mediilor sumelor parțiale. Pentru a fi specific, definiți

$C_n = \frac{s_0 + S_1 + s_2 + \ldots + s_n}{n}$

și definiți însumarea Cesequstro ca fiind limita Cn Ca N merge la infinit. Dacă o serie are o sumă în sensul clasic, ea are și o sumă în sensul Cesextro, iar limitele sunt aceleași. Dar unele serii au o sumă Cesextro care nu au o sumă clasică. Sau poate că există ambele limite, dar etapele intermediare ale însumării Cesextro se comportă mai bine, așa cum vom vedea într-un exemplu de mai jos.

dacă exprimați Cn în termenii originali an Obțineți

$C_n = \sum_{i=0}^n \frac{n-i+1}{N+1} a_i$

cu alte cuvinte, A N-A sumă parțială Cesqustro este o re ponderare a sumelor parțiale clasice, ponderile schimbându-se în funcție de n. rețineți că pentru I fix, fracția care înmulțește ai merge la 1 Pe măsură ce n crește.

însumarea FEJ Oktogr și fenomenul Gibbs

însumarea FEJ Oktogr este însumarea ces Oktogro aplicată seriilor Fourier. Sumele parțiale (obișnuite) ale unei serii Fourier oferă cea mai bună aproximare unei funcții măsurate prin norma celor mai mici pătrate. Dar sumele parțiale Ceseinctro pot fi calitativ mai mult ca funcția fiind aproximată. Demonstrăm acest lucru mai jos cu un val pătrat.

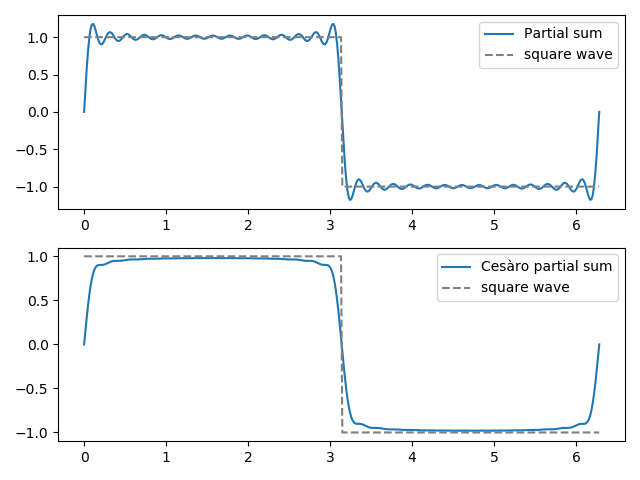
a 30-a sumă parțială obișnuită arată începuturile fenomenului Gibbs, „urechile liliacului” din partea de sus a valului pătrat și imaginea lor în oglindă în partea de jos. Cea de-a 30-a sumă parțială Cesqentro este mai lină și elimină fenomenele Gibbs în apropierea discontinuității în valul pătrat.

mai multe postări din seria Fourier

Seria Fourier-Bessel
contraexemplu la principiul Dirichlet
unde sinusoidale tăiate

KGSAU

Cesextro sumation

însumarea FEJ Oktogr și fenomenul Gibbs

mai multe postări din seria Fourier

Lasă un răspuns Anulează răspunsul