să facem asta. Voi deduce expresia pentru Centrul de masă pentru un triunghi dreptunghic. De ce?

imagine: https://memegenerator.net/instance/57639838/yoda-no-no-there-is-no-why-clear-your-mind-of-questions

vezi, ne vom distra. Am inclus deja un meme Yoda. Ce ar putea merge prost?

aici este triunghiul.

Oh, arată ca un triunghi albastru normal. Corect? Dar să presupunem că aceasta este o foaie subțire de metal cu o masă de M. cum ați găsi locația centrului de masă? Să începem cu definiția de bază a Centrului de masă.

aceasta este în esență o medie ponderată. OK, este o medie ponderată. Dar dacă spargeți obiectul într-o grămadă de bucăți mici, atunci înmulțiți poziția vectorială a fiecărei mase și a masei sale minuscule. Apoi adăugați apoi totul și împărțiți la masa totală. Acesta este centrul de masă. Iată o altă imagine.

desigur, în acest caz nu avem o grămadă de piese. Avem o masă continuă. Asta înseamnă că putem transforma suma într-o integrală. În loc de a face cu atât X și Y-direcții în același timp, am de gând doar să ia în considerare y-Centrul de masă.

voi începe prin a rupe acest triunghi într-o grămadă de dreptunghiuri orizontale. Iată unul dintre acele dreptunghiuri.

deci, pot folosi aceste dreptunghiuri subțiri pentru a găsi centrul de masă. Trebuie doar să înmulțesc poziția fiecărui dreptunghi și masa fiecărui dreptunghi. Poziția este destul de simplă, Este „y”. Masa este un pic mai complicată. De asemenea, observați că pentru dreptunghiurile care se deplasează în sus pe triunghi, acestea sunt mai mici cu o masă mai mică.

aria acestui mic dreptunghi ar trebui să fie proporțională cu aria sa. Permiteți-mi să definesc densitatea zonei pentru întregul triunghi ca:

asta înseamnă că masa dreptunghiului mic va fi valoarea mică (DM) care depinde de aria sa.

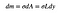
în cele din urmă, trebuie să obțin l în termeni de y. voi face asta obținând mai întâi o expresie în termeni de x. Pot numi partea stângă a dreptunghiului ” x „și partea dreaptă”s”. Aceasta înseamnă că:

dar partea stângă a triunghiului poate fi descrisă ca o linie cu ecuația:

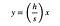
unde (h / S) este panta. Pot rezolva această ecuație pentru x și pot înlocui expresia pentru L.

Ce zici de o verificare rapidă a realității. Să ne asigurăm că lucrurile merg înainte să ajungem prea departe. Ce se întâmplă dacă lăsăm y = h? Aceasta ar trebui să fie în partea de sus a triunghiului cu o lungime de dreptunghi de zero. Da. Asta funcționează. Ce zici de y = 0? Dreptunghiul ar trebui să aibă o lungime de s. arată bine.

acum am nevoie doar pentru a pune toate aceste lucruri împreună. Aceasta este masa acelei felii de dreptunghi.

„s” anulează FTW (pentru victorie).

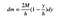
asta e destul de bun pentru acum. Următorul pas este să scrieți o expresie pentru centrul y al masei. Din moment ce voi lăsa lățimea acestei piese să meargă la zero, voi obține o integrală în loc de o sumă.

pot integra acest lucru, dar este mai ușor dacă îl rup în două părți. Doar un pic de algebră îmi dă:

>

acum pot integra. Uite ce primesc.

evaluarea la limitele (care este ușor, deoarece limita inferioară este zero):

boom. Acesta este centrul y al masei. Are chiar unități de distanță (ceea ce ar trebui). De asemenea, observați că centrul de masă y nu depinde de lungimea triunghiului în direcția x (parametrul s). Asta e cool. De asemenea, înseamnă că putem găsi cu ușurință centrul X al masei. Tot ce trebuie să fac este să rup același triunghi în dreptunghiuri verticale.

pentru a face matematica la fel în direcția X, ar trebui să mut originea în celălalt colț al triunghiului. Aceasta înseamnă că centrul de masă x este (1/3) s din partea dreaptă. Aceasta oferă un centru total de masă de:

rece.

calculul numeric al Centrului de Masă

Oh, ai crezut că am terminat? Nu am terminat. Ce zici de asta — un calcul numeric al Centrului de masă? Da, va fi distractiv. Iată planul meu.

• alege dimensiunile reale ale unui triunghi. Nu pot face un calcul numeric cu variabile. Am nevoie de numere. Voi folosi s = 4, h=1. Da, ar trebui să existe unități, dar nu va conta. OK, densitatea zonei este 1 (ar trebui să fie clar că, de asemenea, nu contează).
• alege o dimensiune pas mic. Să presupunem că am blocuri mici cu dimensiunea de 0,01 cu 0,01. Găsiți locația vectorială a acestui bloc și masa acestuia (toate blocurile au aceeași masă).
• utilizați versiunea cu formula sumă a Centrului de masă.
• Deplasați blocul de-a lungul până când toate părțile triunghiului sunt acoperite.

să facem asta. OK, există o mică dificultate. Va trebui să fac o buclă în interiorul unei bucle. Bucla interioară va adăuga pătrate de-a lungul axei x de la panta stângă la x = h. bucla exterioară va muta aceste rânduri orizontale de la 0 la h.

aici este partea principală a codului (codul complet aici):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

cu o dimensiune a piesei de 0,01 pe 0,01, obțin următoarele: