Soma de Cesaro

há mais de uma maneira de somar uma série infinita. A soma de Cesàro permite calcular a soma de séries que não têm uma soma no sentido clássico.

Suponhamos que temos um conjunto infinito

$a_0 + a_1 + a_2 + \cdots$

O n-ésimo soma parcial da série é dado por

$S_n = \sum_{i=0}^n a_i$

O clássico soma da série, se houver, é definido para ser o limite das somas parciais. Isto é,

$\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\to\infty} \sum_{i=0}^n a_i$

de Cesàro tem uma abordagem diferente. Em vez de tomar o limite das somas parciais, toma o limite das médias das somas parciais. Para ser mais específico, a definir

$C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}$

e definir o Cesàro a ser o limite da Cn n vai para o infinito. Se uma série tem uma soma no sentido clássico, ela também tem uma soma no sentido Cesàro, e os limites são os mesmos. Mas algumas séries têm uma soma Cesàro que não tem uma soma clássica. Ou talvez ambos os limites existam, mas os passos intermediários da soma de Cesàro são mais bem comportados, como veremos em um exemplo abaixo.

Se você expressar o Cn em termos de original de um dos termos que você get

$C_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i$

Em outras palavras, o n-ésimo de Cesàro soma parcial é uma nova ponderação do clássico parcial somas, com os pesos a alterar-se em função de n. Note que para fixo, eu, a fração multiplicando ai vai para 1, à medida que n aumenta.

Fejér summation and Gibbs phenomenon

Fejér summation is Cesàro summation applied to Fourier series. As somas parciais (ordinárias) de uma série de Fourier dão a melhor aproximação a uma função medida pela norma dos Mínimos Quadrados. Mas as somas parciais de Cesàro podem ser qualitativamente mais como a função sendo aproximada. Demonstramos isto abaixo com uma onda quadrada.

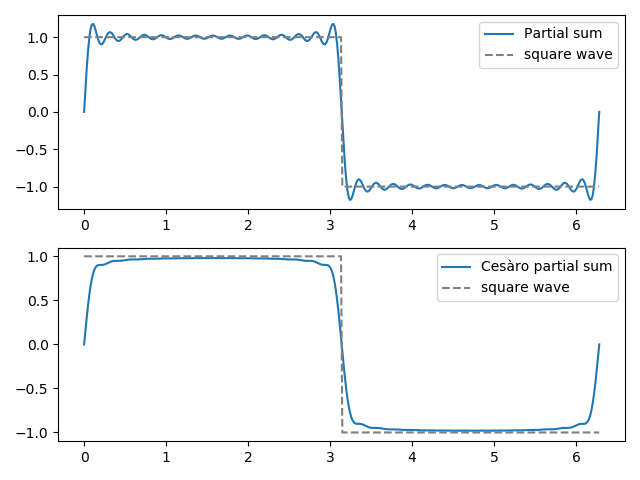
a 30ª soma parcial Ordinária mostra o início do fenômeno Gibbs, as “orelhas de morcego” no topo da Onda Quadrada e sua imagem espelho no fundo. A 30ª soma parcial de Cesàro é mais suave e elimina fenômenos Gibbs perto da descontinuidade na onda quadrada.

mais postos das séries de Fourier

séries de Fourier-Bessel
contra-exemplo do princípio de Dirichlet

ondas sinas recortadas

KGSAU

soma de Cesàro

Fejér summation and Gibbs phenomenon

mais postos das séries de Fourier

Deixe uma resposta Cancelar resposta