Vamos fazer isso. Eu vou derivar a expressão para o centro de massa para um triângulo direito. Por quê?

Veja, nós estamos indo para se divertir. Já incluí um Yoda meme. O que pode correr mal?aqui está o triângulo.

Ah, parece um azul normal triângulo. Certo? Mas suponha que esta é uma fina folha de metal com uma massa de M. Como você encontraria a localização do centro de massa? Vamos começar com a definição básica de centro de massa.

Este é, essencialmente, uma média ponderada. OK, é uma média ponderada. Mas se você quebrar o objeto em um monte de pequenos pedaços, então multiplique a posição vetorial de cada massa e sua pequena massa. Depois adicionas tudo e divides pela massa total. É o centro da massa. Aqui está outra foto.

Claro que neste caso não temos um monte de peças. Temos uma massa contínua. Isso significa que, em vez disso, podemos transformar a soma em uma integral. Em vez de lidar com as direções x e y ao mesmo tempo, vou apenas considerar o y-center da massa.vou começar por quebrar este triângulo num conjunto de rectângulos horizontais. Aqui está um desses retângulos.

Então, Eu posso usar esses magrinhos retângulos para encontrar o centro de massa. Só preciso de multiplicar a posição de cada rectângulo e a massa de cada rectângulo. A posição é bastante simples, é “y”. A missa é um pouco mais complicada. Além disso, observe que para retângulos que se movem para cima do triângulo, eles são menores com massa menor.

a área deste rectângulo minúsculo deve ser proporcional à sua área. Deixe-me definir a área de densidade para todo o triângulo como:

o que significa Que a massa do pequeno retângulo será o valor pequeno (dm) que depende de sua área.

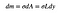
Finalmente, eu preciso para obter L em termos de y. Eu vou fazer o que por primeiro a obtenção de uma expressão em relação a x. Eu posso chamar o lado esquerdo do retângulo ” x “e o lado direito”s”. Isto significa que:

Mas o lado esquerdo do triângulo pode ser descrito como uma linha com a equação:

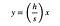
, Onde (h/s) é a inclinação. Eu posso resolver esta equação para x e substituir na expressão para L.

Como a cerca de uma rápida verificação da realidade. Vamos certificar-nos de que as coisas estão a funcionar antes de irmos longe demais. E se deixarmos o y = h? Que deve estar no topo do triângulo com um comprimento retângulo de zero. Sim. Obra. E o y = 0? O retângulo deve ter um comprimento de S. parece bom.agora só preciso de juntar tudo isto. Esta é a massa daquela fatia de um rectângulo.

O “s” cancela FTW (para ganhar).

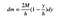
isso é bom o suficiente para agora. O próximo passo é escrever uma expressão para o y-center da massa. Uma vez que vou deixar a largura desta peça ir para zero, vou ter uma integral em vez de uma soma.

posso integrar este, mas é mais fácil se eu quebrá-lo em duas partes. Apenas um pouco de álgebra me dá:

Agora eu posso integrar. Isto é o que eu recebo.

a Avaliação dos limites (o que é fácil, já que o limite inferior é zero):

Boom. É o centro-y da massa. Tem até unidades de distância (que deve ter). Além disso, observe que o y-center de massa não depende do comprimento do triângulo na direção x (o parâmetro s). Isso é fixe. Também significa que podemos facilmente encontrar o x-center de massa. Tudo o que preciso de fazer é quebrar esse mesmo triângulo em rectângulos verticais.

A fim de tornar a matemática o mesmo na direção x, eu precisaria mover a origem para o outro vértice do triângulo. Isto significa que o x-center de massa é (1/3)s do lado direito. Isto dá um total centro de massa de:

Legal.cálculo numérico do centro de massa Oh, pensaste que eu estava acabado? Ainda não acabei. Que tal isto? um cálculo numérico do centro de massa? Sim, vai ser divertido. Eis o meu plano.escolha as dimensões reais de um triângulo. Não posso fazer um cálculo numérico com variáveis. Preciso de números. Vou usar s = 4, h = 1. Sim, deve haver unidades, mas não importa. OK, a densidade da área é 1 (deve ficar claro que também não importa).escolha um pequeno tamanho de passo. Digamos que tenho blocos minúsculos com tamanho de 0,01 Por 0,01. Encontre a localização vetorial deste bloco e sua massa (todos os blocos têm a mesma massa).

Use a versão da fórmula sum do centro de massa.

mova o bloco ao longo até que todas as partes do triângulo estejam cobertas.vamos a isto. Há uma pequena dificuldade. Vou precisar de fazer um loop dentro de um loop. O loop interno será adição de praças ao longo do eixo x da esquerda inclinação para x = h. O loop externo será mover estas linhas horizontais até de 0 a h.

Aqui é a parte principal do código (código completo aqui):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

Com um pedaço do tamanho de 0,01 por 0,01, recebo a seguinte:

Sim, eu estou muito feliz com isso.