sumowanie Cesàro

admin

istnieje więcej niż jeden sposób sumowania nieskończonego szeregu. Sumacja Cesàro pozwala obliczyć sumę szeregów, które nie mają sumy w sensie klasycznym.

Załóżmy, że mamy nieskończony szereg

a_0 + a_1 + a_2 + \cdots

n-ta suma częściowa szeregu jest dana przez

S_n = \sum_{i=0}^N a_i

suma klasyczna szeregu, jeśli istnieje, jest zdefiniowana jako granica jego sum częściowych. Oznacza to, że

\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{N\to\infty} \sum_{i=0}^N a_i

sumowanie Cesàro ma inne podejście. Zamiast brać limit sum częściowych, bierze limit średnich sum częściowych. Aby być konkretnym, zdefiniuj

C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}

i zdefiniuj sumację Cesàro jako granicę Cn, ponieważ n idzie do nieskończoności. Jeśli szereg ma sumę w sensie klasycznym, to ma również sumę w sensie Cesàro, a granice są takie same. Ale niektóre serie mają sumę Cesàro, która nie ma sumy klasycznej. A może oba ograniczenia istnieją, ale kroki pośrednie sumowania Cesàro są lepiej zachowane,jak zobaczymy w poniższym przykładzie.

jeśli wyrażasz Cn w kategoriach oryginalnych terminów an, otrzymujesz

C_n = \sum_{i=0}^N \frac{n-i+1}{n+1} a_i

innymi słowy, N-ta suma częściowa Cesàro jest reweightowaniem klasycznych sum częściowych, przy czym wagi zmieniają się jako funkcja N. zauważ, że dla stałych i, ułamek mnożenia ai idzie do 1 wraz ze wzrostem N.

sumowanie Fejéra i zjawisko Gibbsa

sumowanie Fejéra to sumowanie Cesàro stosowane do szeregów Fouriera. (Zwykłe) sumy cząstkowe szeregu Fouriera dają najlepsze przybliżenie funkcji mierzonej przez normę najmniejszych kwadratów. Ale Sumy cząstkowe Cesàro mogą być jakościowo bardziej zbliżone do funkcji przybliżonej. Demonstrujemy to Poniżej za pomocą fali kwadratowej.

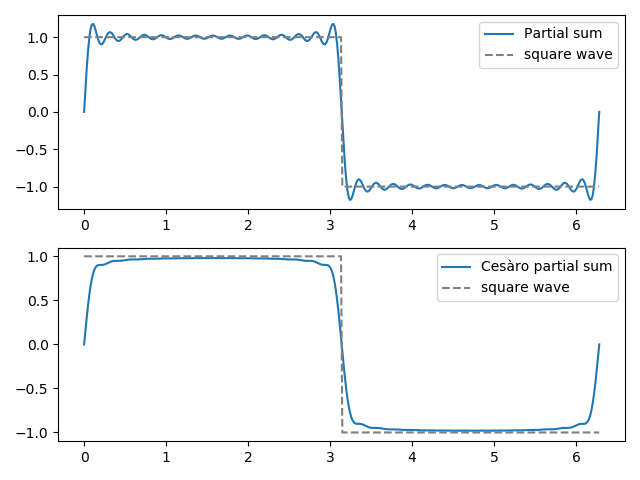
30.zwykła suma cząstkowa pokazuje początki zjawiska Gibbsa, „uszy nietoperza” na górze fali kwadratowej i ich lustrzane odbicie na dole. 30. suma cząstkowa Cesàro jest gładsza i eliminuje zjawiska Gibbsa w pobliżu nieciągłości w fali kwadratowej.

więcej postów serii Fouriera

  • Seria Fouriera-Bessela
  • kontrprzykład do zasady Dirichleta
  • obcięte fale sinusoidalne

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.