jak pamiętasz miejsce na bezludnej wyspie, gdzie zakopałeś swój skarb? Wybierz punkt orientacyjny, powiedzmy palmę i zmierz, ile kroków na północ / południe i ile kroków na wschód / zachód musisz przejść z tego punktu orientacyjnego, aby dostać się do skarbu. To prosty pomysł, ale, co zaskakujące, matematycy potrzebowali wieków, aby rozwinąć jego pełny potencjał w swojej dziedzinie. Kiedy w końcu to zrobili, zrewolucjonizowało matematykę, łącząc dwie dziedziny, które na pierwszy rzut oka mają ze sobą niewiele wspólnego: algebrę i geometrię.
kiedy zaczynamy uczyć się geometrii, zwykle myślimy o prostych kształtach, takich jak linie, trójkąty i okręgi na płaszczyźnie dwuwymiarowej. Te i bardziej skomplikowane kształty można konstruować za pomocą linijki, kompasów i kątomierza. Starożytni Grecy byli mistrzami w tego typu geometrii: używając tylko kompasów i prostej krawędzi (nieoznakowanej linijki) byli w stanie skonstruować szereg kształtów, a nawet mogli udowodnić wyniki matematyczne, takie jak twierdzenie Pitagorasa, za pomocą tych prostych narzędzi.
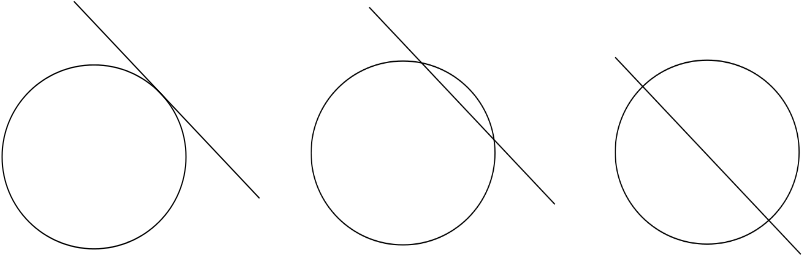
są jednak pewne rzeczy, których nie można zrobić za pomocą tych podstawowych metod. Dwa kształty, na przykład linia i okrąg, mogą się przecinać, ale nie muszą, i mogą się przecinać na różne sposoby: być może linia po prostu dotyka okręgu, być może wygina z niego mały łuk, a może przecina go na pół. Aby zapisać te informacje, potrzebujesz sposobu opisania lokalizacji kształtów.
tu przydaje się pomysł wyspy skarbów. Ilustruje to tzw. układ współrzędnych kartezjańskich. Wybierz punkt na płaszczyźnie, zwany początkiem, i narysuj przez niego dwie prostopadłe osie, jedną poziomą i jedną pionową. Dowolny punkt płaszczyzny można osiągnąć od początku, przemierzając pewną odległość \(x\) wzdłuż osi poziomej i pewną odległość \(y\) wzdłuż osi pionowej. Liczby \((x,y)\) są współrzędnymi punktu. Samo pochodzenie ma współrzędne \((0,0)\). Część osi poziomej(zwana również \(x\)-axis), która leży po lewej stronie początku, oraz część osi pionowej (\(Y\)-axis) poniżej początku są opisane liczbami ujemnymi.
współrzędne kartezjańskie zostały nazwane na cześć XVII-wiecznego francuskiego filozofa i matematyka René Descartesa. Istnieje (prawdopodobnie nieprawdziwa) historia, że Kartezjusz wymyślił te współrzędne, leżąc w łóżku, obserwując muchę na suficie i zastanawiając się, jak opisać jej położenie. Skłonność Kartezjusza do leżenia w łóżku do południa mogła być przyczyną jego śmierci, która miała miejsce w Sztokholmie w 1650 roku. Kartezjusz był w Szwecji jako nauczyciel matematyki Królowej Christiny, która niestety wolała pracować wcześnie rano. Według niektórych doniesień to właśnie te wczesne godziny i skandynawskie temperatury spowodowały zapalenie płuc, które ostatecznie go zabiło. Inni sugerowali, że został otruty przez katolickiego księdza zaniepokojonego radykalną teologią Kartezjusza.
tak czy inaczej, kartezjański układ współrzędnych jest jedną z najważniejszych spuścizn Kartezjusza (choć nie był on jedyną osobą, która miała ten pomysł). Pozwala nam to na rozwiązywanie problemów geometrycznych za pomocą algebry i wizualizację relacji algebraicznych, które w przeciwnym razie byłyby dość abstrakcyjne. Weźmy na przykład równanie \ możemy narysować wykres tej funkcji w kartezjańskim układzie współrzędnych wykreślając wszystkie punkty, których współrzędne mają postać \((x, 2x-1)\): punkty takie jak \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), oraz \((1.73, 2.46)\). W tym przypadku wykres jest linią prostą, która spełnia\(y\)-oś w punkcie \((0, -1)\) i ma nachylenie \(2\).
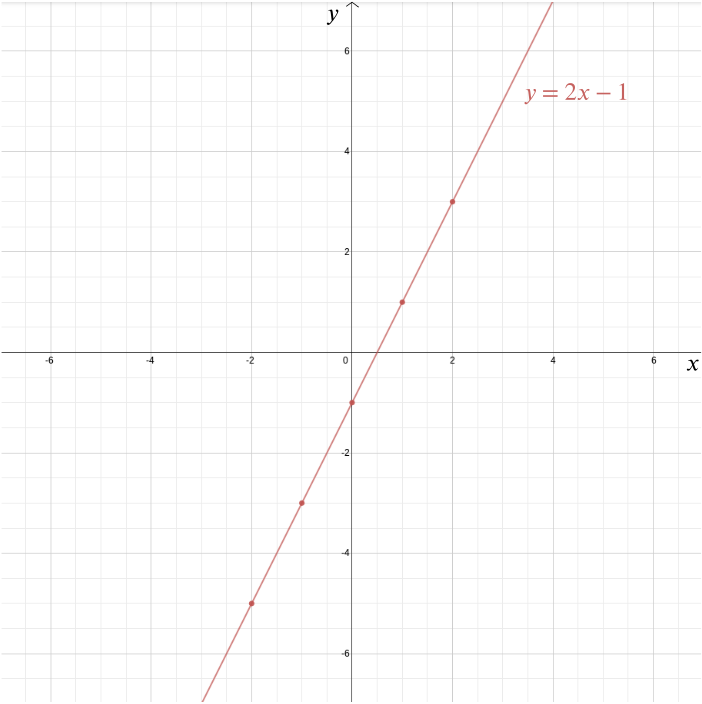
bardziej ogólnie każda linia prosta jest dana równaniem postaci \ gdzie \(M\) daje nachylenie linii,a \((0, b)\) jest punktem, w którym przecina oś \(y\). Pionowa linia, która nie przekracza osi \(y\) – jest dana równaniem postaci \(x=c\). W tym przypadku \((c, 0)\) jest punktem, w którym przecina oś \(x\).
a co z kółkiem? Okrąg składa się ze wszystkich tych punktów, które leżą w równej odległości \(r\) od danego punktu \(m\). Załóżmy, że \(m\) jest punktem \((0,0)\). Z twierdzenia Pitagorasa wiemy, że jeśli punkt \((x, y)\) leży w odległości\ (r\) od\ ((0,0)\), to \
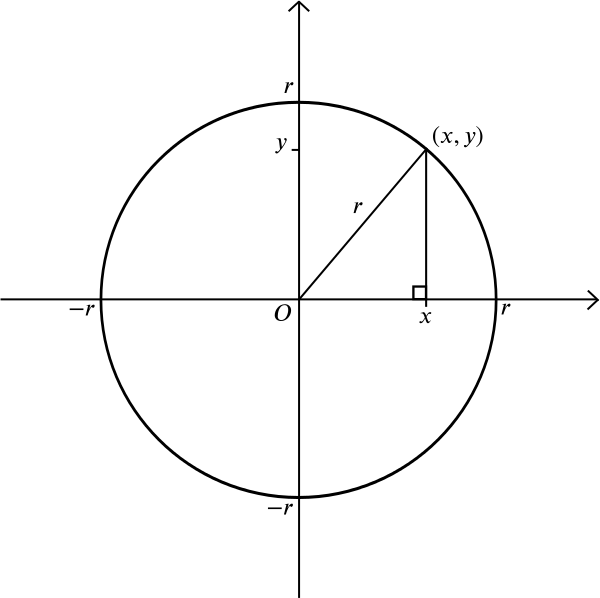
jest to zatem równanie okręgu o promieniu \(r\) wyśrodkowanego na początku. Możesz sam obliczyć, że okrąg o promieniu \(r\) wyśrodkowany na punkcie \((A, b)\) ma równanie \ , ale tutaj jest bardziej skomplikowane pytanie: jaki kształt uzyskasz, gdy weźmiesz pod uwagę wszystkie punkty leżące w równej odległości od danego punktu i danej linii? Bez układu współrzędnych możesz narysować punkt i linię I eksperymentować z linijką lub kompasami. Możesz narysować kilka punktów leżących w równej odległości od obu i zobaczyć, czy możesz odgadnąć ogólny kształt.
jednak odpowiedź staje się o wiele łatwiejsza i bardziej precyzyjna. Załóżmy, że dany punkt znajduje się w odległości \(1\) od podanej linii. Umieśćmy dany punkt na początku i podaną linię tak, aby była pozioma, dana równaniem \ twierdzeniem Pitagorasa odległość dowolnego punktu \((x, y)\) od \((0,0)\) wynosi \(\sqrt{x^2 + y^2}\). Odległość od punktu \((x,y)\) do linii \(y = -1\) wynosi \(|y+1|\) (używamy tutaj wartości bezwzględnej, ponieważ współrzędna \(y\) może być ujemna). Jeśli te dwa są równe, to \ kwadrat obu stron daje \ przestawianie daje \ więc dowolny punkt w równej odległości od punktu \((0,0)\), a linia \(y=-1\) ma współrzędne \(\left (x, \ frac{x^2}{2} – \frac{1}{2}\right)\). Możesz sam sprawdzić, czy konwersja jest również prawdziwa: każdy punkt o tych współrzędnych leży w równej odległości od punktu \((0,0)\) i linii \(y = -1\).
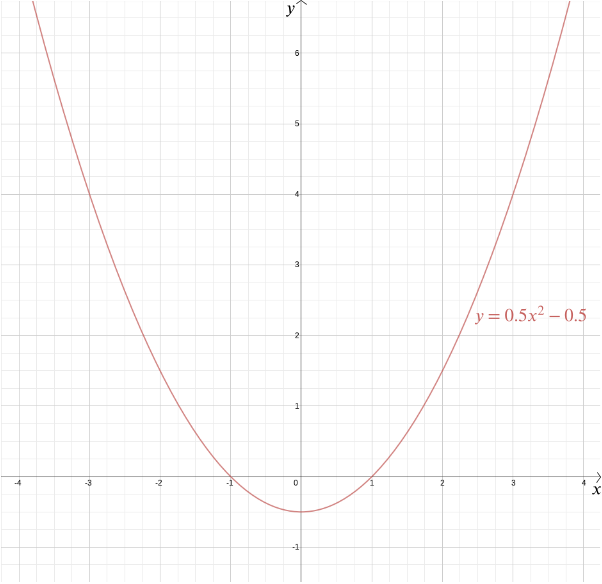
możemy wykreślić wykres tej funkcji, aby zobaczyć wymagany kształt, który okazuje się być parabolą. W rzeczywistości każda funkcja kwadratowa \ for \(a\), \(b\) i \(c\) daje nam parabolę. Ten znajomy kształt, który może występować w tak wielu subtelnych wariantach-długich i cienkich lub przysiadłych i płaskich – jest uchwycony przez to poręczne wyrażenie algebraiczne. Fakt, że dziś terminy „funkcja kwadratowa” i „parabola” są niemal uważane za synonimy, podkreśla, jak udany był pomysł Kartezjusza. Ogólniej, Dowolna zależność algebraiczna pomiędzy dwiema zmiennymi \(x\) i \(y\) daje nam krzywą, którą możemy wykreślić używając współrzędnych kartezjańskich.
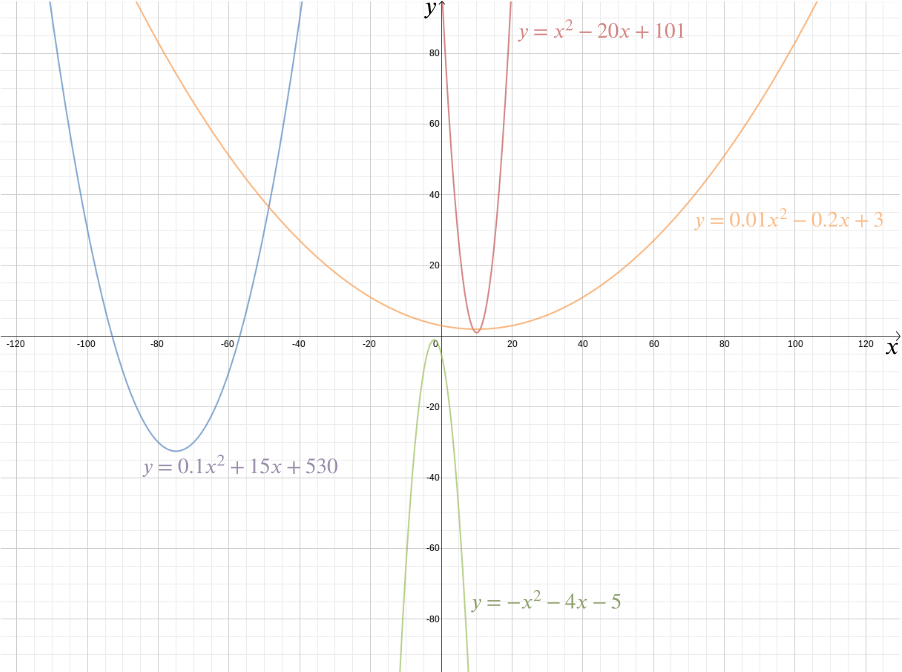
reprezentacja algebraiczna ułatwia odpowiadanie na cały szereg pytań geometrycznych. Aby obliczyć punkty przecięcia linii podane przez \ i parabolę \ (y = \ frac{x^2} {2} – \frac{1}{2}\), po prostu zauważamy,że współrzędna \(y\) dowolnego punktu \((x, y)\) leżącego na obu musi spełniać oba równania, więc \ to daje \ rozwiązywanie równania kwadratowego, które otrzymujemy \ i \ więc punkty przecięcia są w \
oprócz rozwiązywania problemów geometrycznych, współrzędne kartezjańskie pomagają również wizualizować relacje algebraiczne. Załóżmy na przykład, że samochód porusza się z prędkością \(u\), a kierowca hamuje, co skutkuje stałym opóźnieniem, na przykład \(-4\) metrów/sekund\(^2\). Droga zatrzymania \(s\)—odległość, jaką pokonuje samochód, zanim się zatrzyma-jest określona przez zależność algebraiczną \ Wykreślenie tego za pomocą współrzędnych kartezjańskich przynosi do domu to, jak ważne jest spowolnienie w obszarach miejskich, ponieważ droga zatrzymania wzrasta szybko z \(u\).
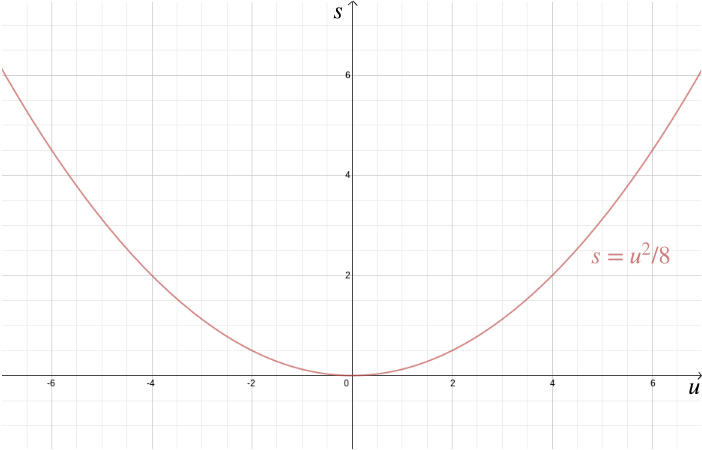
w tym przykładzie znaliśmy zależność między dwiema zmiennymi, ponieważ można ją wyprowadzić z praw fizyki. Ale współrzędne kartezjańskie są również przydatne, gdy podejrzewamy, że dwie zmienne są ze sobą powiązane, ale nie wiemy jak. Załóżmy, że uważamy, że istnieje związek między zyskiem osiągniętym przez Sprzedawcę lodów a temperaturą zewnętrzną. Aby dowiedzieć się, jaka może być ta zależność, możemy zmierzyć temperaturę i zysk w ciągu roku i narysować wartości względem siebie, z temperaturą zarejestrowaną na osi \(x\)-i zyskiem na osi \(y\) -. Możemy wtedy zobaczyć, czy możemy dostrzec wzór. Na pierwszym diagramie poniżej możemy się domyślać, że relacja jest liniowa i możemy spróbować znaleźć linię prostą\, która najlepiej pasuje do naszych danych (istnieją metody na znalezienie tego najlepszego dopasowania). Na drugim diagramie poniżej możemy zgadnąć, że relacja jest kwadratowa i ponownie możemy spróbować znaleźć funkcję \, która najlepiej pasuje do danych.
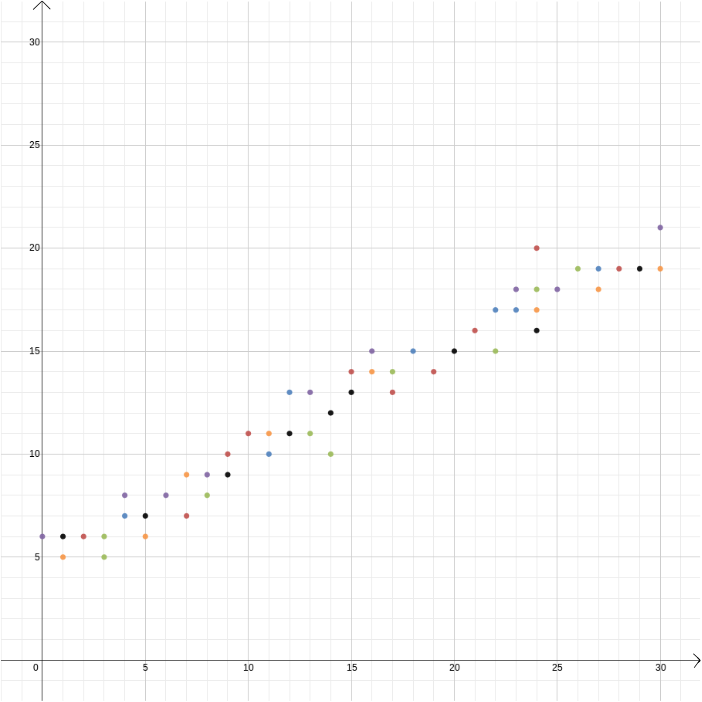
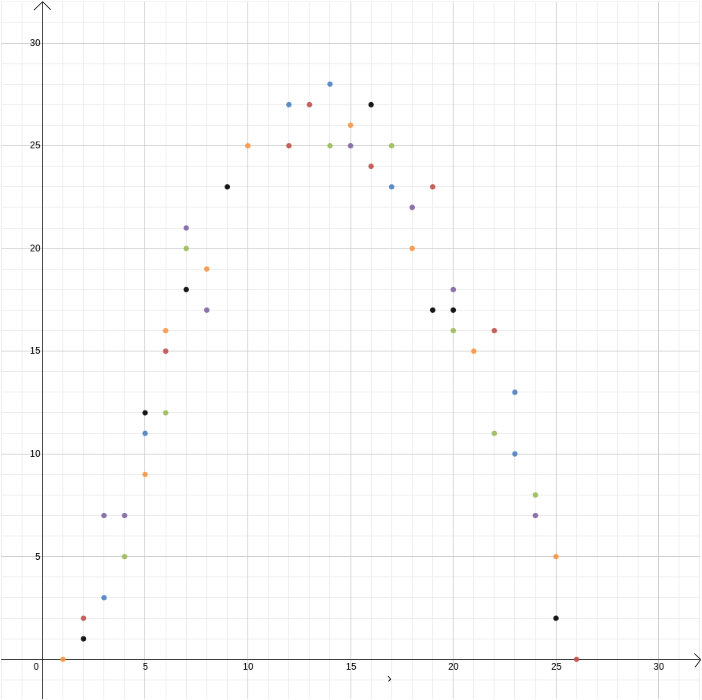
współrzędne kartezjańskie odegrały ważną rolę w rozwoju rachunku w drugiej połowie XVII wieku. Rachunek matematyczny umożliwia obliczenie atrybutów krzywych, takich jak ich nachylenie w danym punkcie lub obszar obszaru leżącego między krzywą a osią \(x\). Mogą one mieć również fizyczne interpretacje. Na przykład, jeśli wykreślimy odległość przejechaną przez samochód względem czasu, w którym się poruszał, nachylenie krzywej wynikowej w danym czasie—szybkość zmiany odległości względem czasu-reprezentuje prędkość, z jaką samochód podróżował w tym momencie w czasie: jest pochodną funkcji, która daje nam odległość w kategoriach czasu. Zobacz też dlaczego gradienty są ważne w realnym świecie?.
możemy również pójść w górę wymiaru, rozważając trzecią oś prostopadłą do dwóch pierwszych, którą można sobie wyobrazić jako wychodzącą z kartki papieru i wskazującą na Ciebie. Korzystając z takiego trójwymiarowego systemu możesz teraz reprezentować trójwymiarowe obiekty i wizualizować, jak trzecia zmienna \(z\) zależy od dwóch pierwszych, \(x\) i \(y\).
te przykłady powinny dać ci poczucie, dlaczego współrzędne stały się tak niezbędne we wszystkich dziedzinach nauki, od fizyki po astronomię i inżynierię, a także w przemyśle wizualnym do produkcji grafiki komputerowej i obrazów generowanych komputerowo, które podziwiamy w filmach i grach.
w samej matematyce związek między algebrą a geometrią rozwinął się w cały obszar zwany geometrią algebraiczną, który posiada własną fascynację. Być może najbardziej znanym wynikiem, który wyłonił się z tego obszaru jest ostatnie twierdzenie Fermata, nazwane na cześć współczesnego Kartezjusza, Pierre ’ a de Fermata, który również znacząco przyczynił się do rozwoju kartezjańskiego układu współrzędnych. Fermat rozważał zagadnienie łączące geometrię z teorią liczb. Zgodnie z twierdzeniem Pitagorasa, jeśli \(A\), \(b\) i \(c\) są bokami trójkąta prostokątnego, a \(c\) jest bokiem przeciwnym do kąta prostego, to \(a^2 + b^2 = c^2\). Istnieje nieskończenie wiele trójek liczb całkowitych \(a\), \(b\) i \(c\), które spełniają tę zależność; \((3,4,5)\) jest przykładem.
Załóżmy teraz, że zmienimy wykładnik i rozważymy wyrażenia takie jak \ i \ i bardziej ogólnie \ gdzie \(n\) jest liczbą naturalną większą niż \(2\). Czy nadal możemy znaleźć dodatnie liczby całkowite \(A\), \(b\) I \(c\) spełniające równanie? FERMAT podejrzewał, że nie możemy i nabazgrał tyle na marginesie swojego podręcznika do matematyki, mówiąc, że ma „cudowny dowód” na ten fakt, że margines był zbyt wąski, aby go zawrzeć.
to bazgroły miały nawiedzać matematyków przez ponad 350 lat. Dopiero w 1994 roku poprawny dowód tego pozornie nieszkodliwego wyniku został ostatecznie ogłoszony przez matematyka Andrew Wilesa. Wiles szeroko wykorzystywał geometrię algebraiczną. W szczególności wykorzystał wyniki dotyczące krzywych eliptycznych opisywanych przez punkty na płaszczyźnie, których współrzędne spełniają \ Descartes’ kontemplacja muchy przebyła długą drogę!
