zróbmy to. Wyprowadzę wyrażenie dla środka masy dla trójkąta prostokątnego. Dlaczego?

Dodałem już mem Yody. Co może pójść nie tak?
oto Trójkąt.

och, wygląda jak normalny niebieski trójkąt. Prawda? Ale załóżmy, że jest to cienka blacha o masie M. Jak można znaleźć położenie środka masy? Zacznijmy od podstawowej definicji środka masy.

jest to zasadniczo średnia ważona. OK, to jest średnia ważona. Ale jeśli rozbijemy obiekt na kilka małych kawałków, pomnożymy pozycję wektorową każdej masy i jej małej masy. Następnie dodajemy wszystko i dzielimy przez masę całkowitą. To środek masy. Tu jest kolejne zdjęcie.

oczywiście w tym przypadku nie mamy kilku kawałków. Mamy masę ciągłą. Oznacza to, że zamiast tego możemy zamienić sumę w całkę. Zamiast zajmować się jednocześnie kierunkami x i y, rozważę po prostu y-środek masy.
zacznę od rozbicia tego trójkąta na kilka poziomych prostokątów. Oto jeden z tych prostokątów.

więc mogę użyć tych chudych prostokątów, aby znaleźć środek masy. Muszę tylko pomnożyć położenie każdego prostokąta i masę każdego prostokąta. Pozycja jest dość prosta, to „y”. Masa jest nieco bardziej skomplikowana. Zauważ też, że dla prostokątów, które poruszają się w górę trójkąta, są one mniejsze o mniejszej masie.
powierzchnia tego małego prostokąta powinna być proporcjonalna do jego powierzchni. Zdefiniuję gęstość obszaru dla całego trójkąta jako:


oznacza to, że masa małego prostokąta będzie małą wartością (DM), która zależy od jego powierzchni.
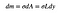
wreszcie, muszę dostać l pod względem y. zrobię to, najpierw dostając wyrażenie pod względem x. Mogę nazwać lewą stronę prostokąta „x” i prawą stronę „s”. Oznacza to, że:

ale lewy bok tego trójkąta można opisać jako linię z równaniem:
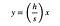
gdzie (h/S) jest nachyleniem. Mogę rozwiązać to równanie dla x i podstawić do wyrażenia dla L.

co powiesz na szybkie sprawdzenie rzeczywistości. Upewnijmy się, że wszystko działa, zanim zajdziemy za daleko. Co jeśli pozwolimy y = h ? To powinno być na górze trójkąta o długości prostokąta równej zero. Tak. To działa. A co z y = 0? Prostokąt powinien mieć długość s.wygląda dobrze.
teraz muszę to wszystko poskładać do kupy. To jest masa tego kawałka prostokąta.

„s” anuluje FTW (za wygraną).
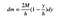
na razie wystarczy. Następnym krokiem jest napisanie wyrażenia dla y-środka masy. Ponieważ pozwolę, aby szerokość tego elementu wynosiła zero, otrzymam całkę zamiast sumy.
mogę to zintegrować, ale będzie łatwiej, jeśli podzielę go na dwie części. Tylko trochę algebry daje mi:
teraz mogę się zintegrować. Oto, co dostaję.

Ocena na granicy (co jest łatwe, ponieważ dolna granica wynosi zero):

Boom. To Y jest środkiem masy. Ma nawet jednostki odległości (tak jak powinno być). Zauważ również, że środek masy y nie zależy od długości trójkąta w kierunku x (Parametr s). Spoko. Oznacza to również, że możemy łatwo znaleźć x-Środek masy. Wszystko, co muszę zrobić, to rozbić ten sam trójkąt na pionowe prostokąty.

aby matematyka była taka sama w kierunku X, musiałbym przenieść początek do drugiego rogu trójkąta. Oznacza to, że x-Środek masy wynosi (1/3)s od prawej strony. Daje to całkowity środek masy:

fajne.
Numeryczne Obliczanie środka masy
och, myślałeś, że skończyłem? Jeszcze nie skończyłem. Co powiesz na to — numeryczne obliczenie środka masy? Tak, będzie fajnie. Oto mój plan.
- Wybierz rzeczywiste wymiary trójkąta. Nie mogę wykonywać obliczeń numerycznych ze zmiennymi. Potrzebuję liczb. Użyję s = 4, h = 1. Tak, powinny być jednostki, ale to nie ma znaczenia. Ok, gęstość obszaru wynosi 1 (powinno być jasne, że również nie ma znaczenia).
- wybierz mały rozmiar kroku. Powiedzmy, że mam małe bloki o rozmiarze 0,01 na 0,01. Znajdź położenie wektorowe tego bloku i jego masę (wszystkie bloki mają tę samą masę).
- użyj wzoru sumy środka masy.
- Przesuń blok wzdłuż, aż wszystkie części trójkąta zostaną pokryte.
zróbmy to. OK, jest mały problem. Muszę zrobić pętlę wewnątrz pętli. Wewnętrzna pętla będzie sumować kwadraty wzdłuż osi x z lewego zbocza do x = h. zewnętrzna pętla będzie przesuwać te poziome rzędy w górę od 0 do h.
oto główna część kodu (Pełny kod tutaj):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
przy rozmiarze kawałka 0.01 na 0.01 otrzymuję następujące:

tak, i jestem z tego zadowolony.
