laten we dit doen. Ik ga de uitdrukking afleiden voor het middelpunt van de massa voor een rechthoekige driehoek. Waarom?

zie, we gaan plezier hebben. Ik heb al een Yoda meme toegevoegd. Wat kan er mis gaan?
Hier is de driehoek.

Oh, ziet eruit als een normale blauwe driehoek. Toch? Maar stel dat dit een dunne metalen plaat is met een massa van M. hoe zou je de locatie van het middelpunt van de massa vinden? Laten we beginnen met de basisdefinitie van het middelpunt van de massa.

Dit is in wezen een gewogen gemiddelde. OK, het is een gewogen gemiddelde. Maar als je het object in kleine stukjes breekt, vermenigvuldig dan de vectorpositie van elke massa en zijn kleine massa. Dan tel je alles op en deel je door de totale massa. Dat is het middelpunt van de massa. Hier is nog een foto.

natuurlijk hebben we in dit geval geen aantal stukken. We hebben een continue massa. Dat betekent dat we de som in plaats daarvan tot een integraal kunnen maken. In plaats van zowel de x-als de y-richtingen tegelijkertijd te behandelen, ga ik gewoon het Y-centrum van massa overwegen.
Ik begin met het breken van deze driehoek in een aantal horizontale rechthoeken. Hier is een van die rechthoeken.

dus ik kan deze magere rechthoeken gebruiken om het middelpunt van de massa te vinden. Ik hoef alleen maar de positie van elke rechthoek en de massa van elke rechthoek te vermenigvuldigen. De positie is vrij eenvoudig, het is “y”. De massa is wat lastiger. Merk ook op dat Voor rechthoeken die omhoog de driehoek bewegen, ze kleiner zijn met kleinere massa.
De oppervlakte van deze kleine rechthoek moet proportioneel zijn aan de oppervlakte. Laat me de oppervlaktedichtheid voor de hele driehoek definiëren als:

dat betekent dat de massa van de minuscule rechthoek de minuscule waarde (DM) is die afhankelijk is van de oppervlakte.
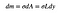
tot slot, ik moet l krijgen in termen van y. Ik zal dat doen door eerst een uitdrukking te krijgen in termen van X. Ik kan de linkerkant van Rechthoek “x” en de rechterkant “s”noemen. Dit betekent dat:

Maar de linker zijde van die driehoek kan beschreven worden als een lijn met de vergelijking:
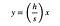
Waar (h/s) is de helling. Ik kan deze vergelijking voor x oplossen en vervangen door de uitdrukking voor L.

wat dacht je van een snelle reality check. Laten we ervoor zorgen dat alles werkt voordat we te ver gaan. Wat als we y = h toelaten? Dat moet aan de bovenkant van de driehoek met een rechthoek lengte van nul. Yup. Dat werkt. En y = 0? De rechthoek moet een lengte van s hebben. ziet er goed uit.
nu hoef ik alleen maar al deze dingen samen te stellen. Dit is de massa van dat stuk van een rechthoek.

De “s” annuleert FTW (voor de overwinning).
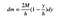

Ik kan dit integreren, maar het is makkelijker als ik het in twee delen opmaak. Een klein beetje algebra geeft me:

nu kan ik integreren. Dit is wat ik krijg.

het Evalueren van de grenzen (dat is eenvoudig omdat de ondergrens is nul):

Boem. Dat is het Y-centrum van de massa. Het heeft zelfs eenheden van afstand (die het zou moeten). Merk ook op dat het Y-centrum van massa niet afhangt van de lengte van de driehoek in de x-richting (de parameter s). Dat is cool. Het betekent ook dat we gemakkelijk het X-centrum van massa kunnen vinden. Het enige wat ik moet doen is diezelfde driehoek in verticale rechthoeken breken.

om de wiskunde in de x-richting hetzelfde te maken, moet ik de oorsprong verplaatsen naar de andere hoek van de driehoek. Dit betekent dat het X-centrum van massa (1/3) s van de rechterkant is. Dit geeft een totale massa van:

cool.
numerieke berekening van het middelpunt van de massa
Oh, dacht je dat ik klaar was? Ik ben nog niet klaar. Wat dacht je hiervan-een numerieke berekening van het middelpunt van de massa? Ja, het wordt leuk. Dit is mijn plan.
- kies werkelijke afmetingen van een driehoek. Ik kan geen numerieke berekening maken met variabelen. Ik heb nummers nodig. Ik ga s = 4 gebruiken, h = 1. Ja, er zouden eenheden moeten zijn, maar dat maakt niet uit. OK, de oppervlaktedichtheid is 1 (Het moet duidelijk zijn dat het ook niet uitmaakt).
- Kies een kleine stapgrootte. Laten we zeggen dat ik kleine blokken heb met een grootte van 0,01 bij 0,01. Zoek de vectorlocatie van dit blok en zijn massa (alle blokken hebben dezelfde massa).
- gebruik de somformuleversie van het middelpunt van de massa.
- beweeg het blok mee totdat alle delen van de driehoek bedekt zijn.
laten we dit doen. Oké, er is een klein probleem. Ik moet een lus in een lus doen. De binnenste lus toe te voegen vierkanten langs de x-as van de linker helling in x = h. De buitenste lus zal worden is het verplaatsen van deze horizontale rijen-up van 0 tot en met h.
Hier is het belangrijkste deel van de code (volledige tekst hier):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
Met een stuk grootte van 0,01 0,01 lager, krijg ik het volgende:

Ja, ik ben er erg blij mee.
