Cesàro sommatie

admin

Er is meer dan één manier om een oneindige reeks op te tellen. Cesàro sommatie kunt u berekenen van de som van de series die geen Som in de klassieke zin.

stel dat we een oneindige reeks hebben

a_0 + a_1 + a_2 + \cdots

De nde gedeeltelijke som van de reeks wordt gegeven door

S_n = \sum_{i=0}^n a_i

de klassieke som van de reeks, indien deze bestaat, wordt gedefinieerd als de limiet van de deelbedragen. Dat wil zeggen:

\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\to\infty} \sum_{i=0}^n a_i

cesàro-sommatie hanteert een andere benadering. In plaats van de limiet van de gedeeltelijke bedragen te nemen, neemt het de limiet van de gemiddelden van de gedeeltelijke bedragen. Om specifiek te zijn, definieer

C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}

en definieer de Cesàro-som als de limiet van de Cn als n naar oneindig gaat. Als een reeks een Som in de klassieke zin heeft, heeft ze ook een Som in de Cesàro zin, en de grenzen zijn hetzelfde. Maar sommige series hebben een Cesàro som die geen klassieke Som hebben. Of misschien beide grenzen bestaan, maar de tussenliggende stappen van cesàro sommatie zijn beter gedragen, zoals we zullen zien in een voorbeeld hieronder.

Als u uitdrukkelijk de Cn in termen van de oorspronkelijke een algemene krijgt u

C_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i

In andere woorden, de n-Cesàro gedeeltelijke som is een nieuwe weging van de klassieke gedeeltelijke sommen, met de gewichten veranderen als functie van n. Merk op dat voor vaste i, de fractie vermenigvuldigen ai gaat naar 1 als n toeneemt.

Fejér-sommatie en Gibbs-fenomeen

Fejér-sommatie is Cesàro-sommatie toegepast op fourierreeksen. De (gewone) partiële sommen van een fourierreeks geven de beste benadering van een functie zoals gemeten door de kleinste kwadratennorm. Maar de Cesàro partiële sommen kunnen kwalitatief meer lijken op de functie die wordt benaderd. We demonstreren dit hieronder met een vierkante golf.

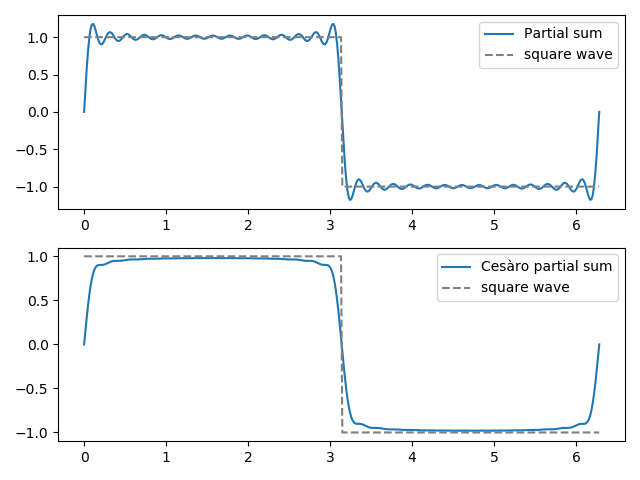
de 30e gewone partiële Som toont het begin van het Gibbs-fenomeen, de” vleermuisoren ” bovenaan de vierkante golf en hun spiegelbeeld onderaan. De 30e Cesàro gedeeltelijke som is gladder en elimineert Gibbs verschijnselen in de buurt van de discontinuïteit in de vierkante golf.

meer berichten uit de Fourierreeks

  • Fourier-Besselreeks
  • tegenvoorbeeld van het Dirichlet-Principe
  • geknipte sinusgolven

Geef een antwoord

Het e-mailadres wordt niet gepubliceerd.