hoe herinnert u zich de plek op een onbewoond eiland waar u uw schat hebt begraven? Je kiest een landmark, zeg een palmboom, en meet hoeveel stappen noord / zuid en hoeveel stappen Oost/west je moet gaan van dat landmark om bij de schat te komen. Het is een eenvoudig idee, maar verrassend genoeg deden wiskundigen er eeuwen over om het volledige potentieel in hun eigen vakgebied te ontwikkelen. Toen ze dat uiteindelijk deden, veranderde het de wiskunde door twee gebieden samen te brengen die op het eerste gezicht weinig met elkaar te maken hebben: algebra en meetkunde.
wanneer we meetkunde beginnen te leren denken we meestal aan eenvoudige vormen zoals lijnen, driehoeken en cirkels in het tweedimensionale vlak. Je kunt deze en meer gecompliceerde vormen construeren met behulp van een liniaal, kompassen en gradenboog. De oude Grieken waren meesters in dit type meetkunde: met behulp van kompassen en een straight-edge (een ongemarkeerde liniaal) waren ze in staat om een reeks vormen te construeren en ze konden zelfs wiskundige resultaten bewijzen, zoals de stelling van Pythagoras, met behulp van deze eenvoudige hulpmiddelen.
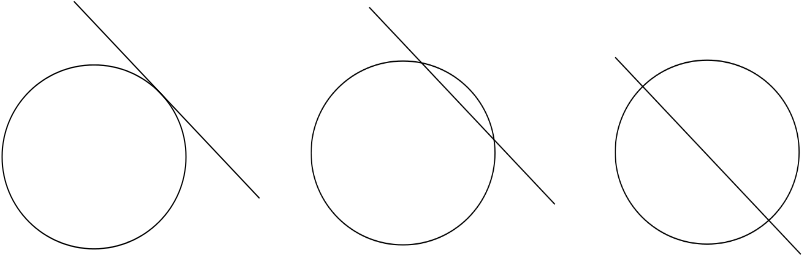
Er zijn echter bepaalde dingen die u niet kunt doen met deze basismethoden. Twee vormen, bijvoorbeeld een lijn en een cirkel, kunnen al dan niet kruisen, en ze kunnen elkaar op verschillende manieren snijden: misschien raakt de lijn gewoon de cirkel, misschien scheert hij er een kleine boog van af, of misschien snijdt hij hem doormidden. Om deze informatie vast te leggen moet je een manier om de locaties van de vormen te beschrijven.
Hier komt het idee van treasure island van pas. Het illustreert wat het Cartesiaanse coördinatenstelsel wordt genoemd. Kies een punt in het vlak, genaamd de oorsprong, en teken twee loodrechte assen door het, een horizontale en een verticale. Elk punt in het vlak kan vanaf de oorsprong worden bereikt door een bepaalde afstand \(x\) langs de horizontale as en een bepaalde afstand \(y\) langs de verticale as te nemen. De getallen \((x, y)\) zijn de coördinaten van het punt. De oorsprong zelf heeft coördinaten \((0,0)\). Het deel van de horizontale as (ook wel de \(x\)-as genoemd) dat links van de oorsprong ligt en het deel van de verticale as (de \(y\)-as) onder de oorsprong worden beschreven door negatieve getallen.
Cartesiaanse coördinaten zijn vernoemd naar de 17e-eeuwse Franse filosoof en wiskundige René Descartes. Er is een (waarschijnlijk onwaar) verhaal dat Descartes deze coördinaten uitvond terwijl hij in bed lag te kijken naar een vlieg op het plafond en zich afvraagt hoe hij de locatie moet beschrijven. Descartes ‘ voorliefde om tot het middaguur in bed te liggen kan de oorzaak zijn geweest van zijn overlijden, die in Stockholm in 1650 plaatsvond. Descartes was in Zweden om op te treden als wiskundeleraar van koningin Christina, die helaas liever vroeg in de ochtend werkte. Volgens sommige rapporten waren het deze vroege uren en de Scandinavische temperaturen die de longontsteking veroorzaakten die hem uiteindelijk doodde. Anderen hebben gesuggereerd dat hij werd vergiftigd door een katholieke priester die zich zorgen maakte over Descartes’ radicale theologie.
hoe dan ook, het Cartesiaanse coördinatenstelsel is een van de belangrijkste legaten van Descartes (hoewel hij niet de enige was die het idee had). Het stelt ons in staat om meetkundige problemen te beantwoorden met behulp van algebra en om algebraïsche relaties te visualiseren die anders vrij abstract zouden blijven. Neem bijvoorbeeld de vergelijking \ we kunnen de grafiek van deze functie in een Cartesiaans coördinatenstelsel plotten door alle punten te plotten waarvan de coördinaten de vorm \((x,2x-1)\)hebben: punten zoals \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), en \((1.73, 2.46)\). In dit geval is de grafiek een rechte lijn die de \(y\)-as op het punt \((0,-1)\) ontmoet en een helling van \(2\) heeft.
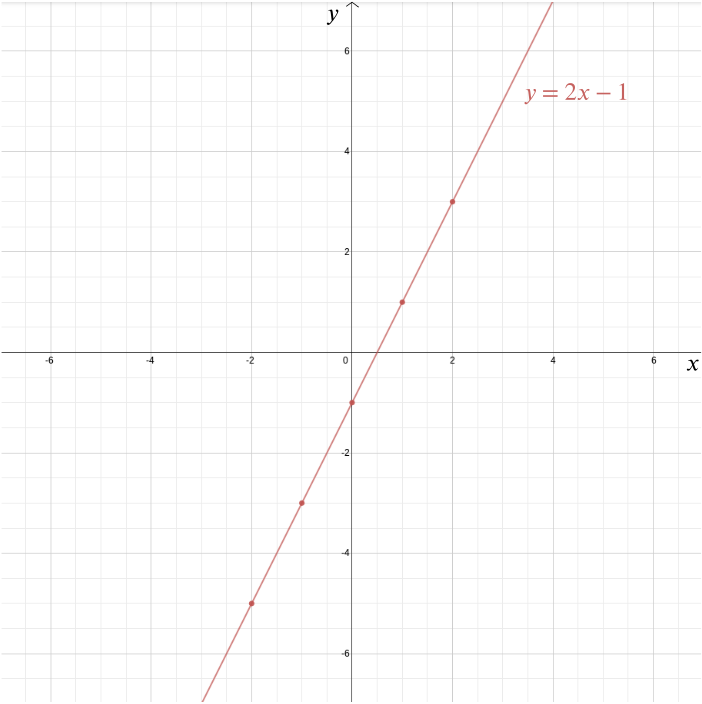
meer in het algemeen wordt elke rechte gegeven door een vergelijking van de vorm \ waar \(m\) je de helling van de lijn geeft en \((0,b)\) het punt is waarop hij de \(y\)-as kruist. Een verticale lijn die niet de \(y\)-as kruist wordt gegeven door een vergelijking van de vorm \(x=c\). In dit geval is \((c,0)\) het punt waarop het de \(x\)-as kruist.
hoe zit het met een cirkel? Een cirkel bestaat uit al die punten die op gelijke afstand \(r\) van een gegeven punt \(m\) liggen. Laten we aannemen dat \(m\) het punt \((0,0)\) is. Uit de stelling van Pythagoras weten we dat als een punt \((x, y)\) op afstand \(r\) van \((0,0)\) ligt, dan \
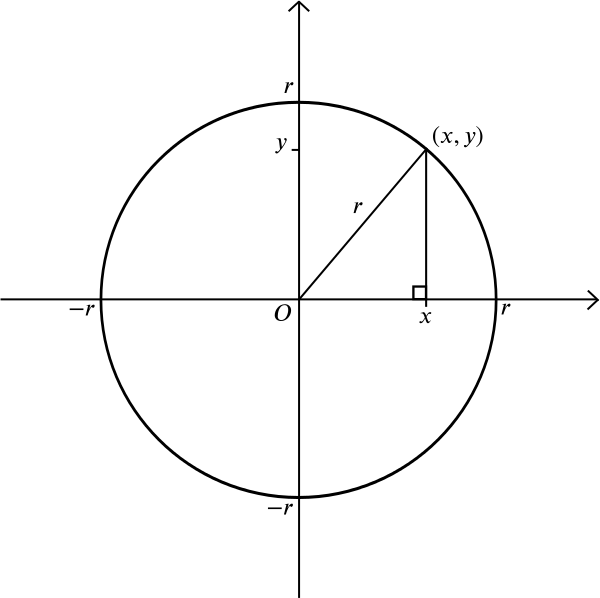
Dit is daarom de vergelijking van een cirkel met straal \(r\) gecentreerd op de oorsprong. Je kunt voor jezelf uitrekenen dat een cirkel van straal \(r\) gecentreerd op het punt \((A, b)\) de vergelijking \ heeft maar hier is een ingewikkelder vraag: welke vorm krijg je als je alle punten in aanmerking neemt die op gelijke afstand liggen van een gegeven punt en een gegeven lijn? Zonder coördinatenstelsel zou je het punt en de lijn kunnen tekenen en experimenteren met je liniaal of kompas. Je zou een paar punten kunnen tekenen die op een gelijke afstand van beide liggen en kijken of je de algemene vorm kunt raden.
gewapend met een coördinatenstelsel wordt het antwoord echter een stuk eenvoudiger en veel preciezer. Stel dat het gegeven punt zich op afstand \(1\) van de gegeven lijn bevindt. Laten we het gegeven punt op de oorsprong en de gegeven lijn plaatsen zodat het horizontaal is, gegeven door de vergelijking \ door de stelling van Pythagoras de afstand van elk punt \((x,y)\) van \((0,0)\) is \(\sqrt{x^2 + y^2}\). De afstand van een punt \((x, y)\) tot de lijn \(y = -1\) is \(|y+1|\) (We gebruiken hier de absolute waarde omdat de \(y\)-coördinaat negatief kan zijn). Als die twee gelijk zijn, dan geeft \ Squaring beide zijden \ herschikken \ dus elk punt op gelijke afstand van het punt \((0,0)\) en de lijn \(y=-1\) heeft coördinaten \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Je kunt zelf controleren of het omgekeerde ook Waar is: elk punt met deze coördinaten ligt op gelijke afstand van het punt \((0,0)\) en de lijn \(y=-1\).
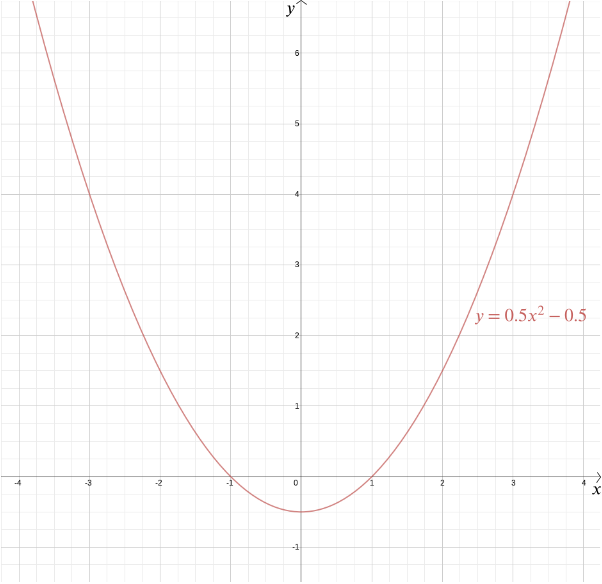
We kunnen de grafiek van deze functie plotten om de gewenste vorm te zien, die een parabool blijkt te zijn. In feite geeft elke kwadratische functie \ voor \(A\), \(b\) en \(c\) constanten, ons een parabool. Deze bekende vorm, die kan komen in zo veel subtiele variaties-lang en dun of squat en plat—wordt gevangen door deze handige algebraïsche expressie. Het feit dat vandaag de dag de termen “kwadratische functie” en “parabool” bijna als synoniem worden beschouwd, benadrukt hoe succesvol het idee van Descartes is geweest. Meer in het algemeen geeft elke algebraïsche relatie tussen twee variabelen \(x\) en \(y\) ons een curve die we kunnen plotten met behulp van cartesiaanse coördinaten.
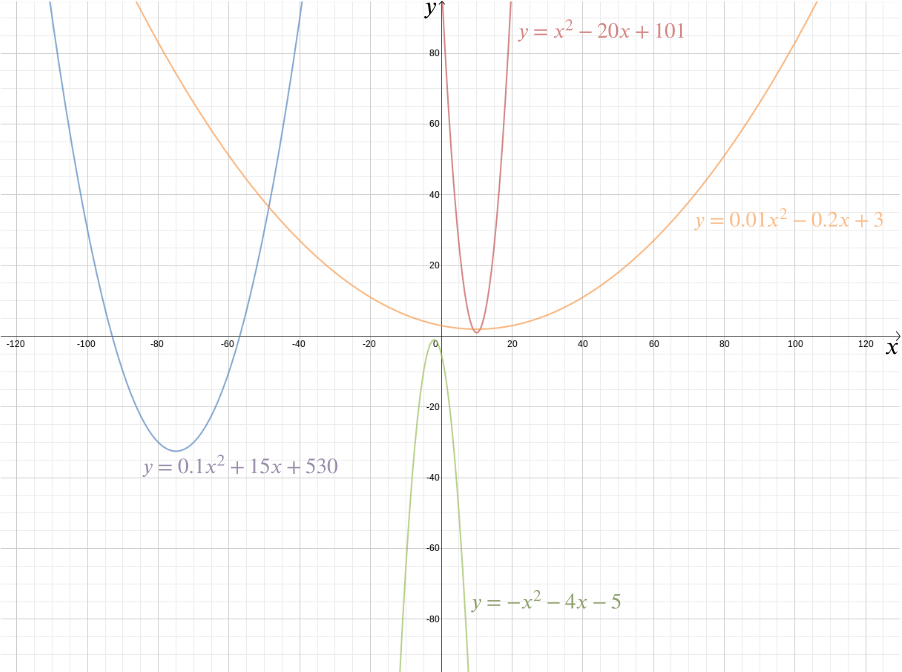
de algebraïsche representatie maakt het gemakkelijk om een hele reeks meetkundige vragen te beantwoorden. Om de snijpunten uit te werken van de lijn gegeven door \ en de parabool \(y = \ frac{x^2}{2} – \ frac{1}{2}\), merken we gewoon op dat de \(y\) coördinaat van elk punt \((x, y)\) dat op beide ligt aan beide vergelijkingen moet voldoen, dus \ dit geeft \ het oplossen van de kwadratische vergelijking die we krijgen \ en \ dus de snijpunten zijn op \
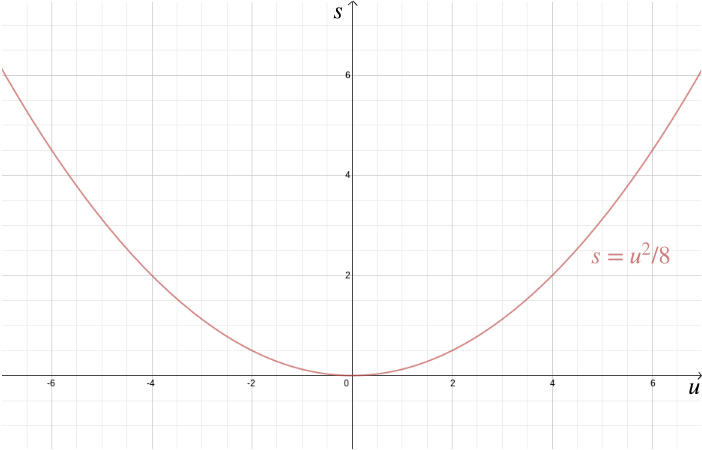
behalve het oplossen van meetkundige problemen, helpen Cartesische coördinaten ook om algebraïsche relaties te visualiseren. Stel bijvoorbeeld dat een auto met snelheid \(u\) rijdt en de bestuurder remt, wat resulteert in een constante vertraging van bijvoorbeeld \(-4\) meter/seconde\(^2\). De remafstand \(s\)—de afstand die de auto aflegt voordat hij tot stilstand komt-wordt gegeven door de algebraïsche relatie \ door dit met behulp van cartesiaanse coördinaten uit te zetten, wordt duidelijk hoe belangrijk het is om in stedelijke gebieden te vertragen, omdat de remafstand snel toeneemt met \(u\).
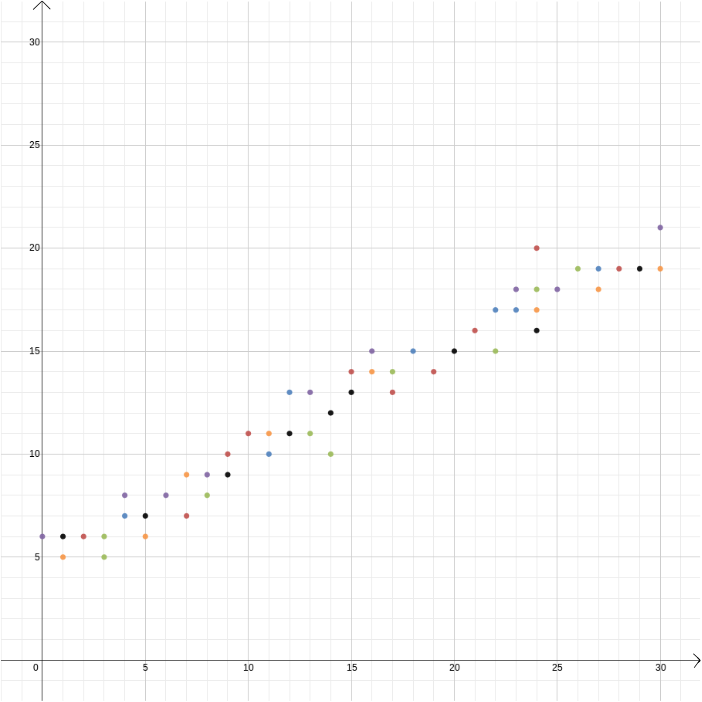
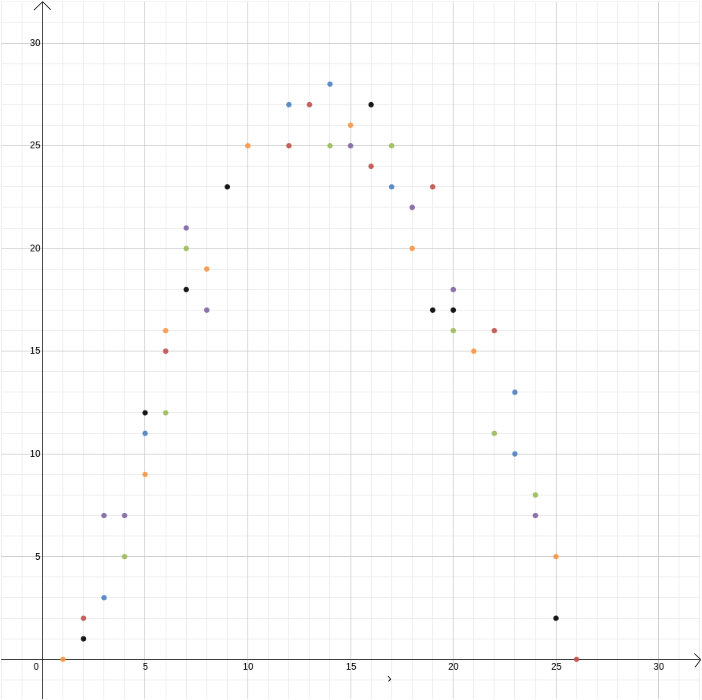
in dit voorbeeld kenden we de relatie tussen twee variabelen omdat het kan worden afgeleid uit de wetten van de fysica. Maar Cartesiaanse coördinaten zijn ook handig als je vermoedt dat twee variabelen gerelateerd zijn, maar je weet niet hoe. Stel dat we denken dat er een relatie is tussen de winst van een ijsverkoper en de buitentemperatuur. Om uit te vinden wat die relatie zou kunnen zijn, kunnen we temperatuur en winst meten over bijvoorbeeld de loop van een jaar en de waarden tegen elkaar plotten, waarbij de temperatuur op de \(x\)-as wordt geregistreerd en de winst op de \(y\)-as. Dan kunnen we zien of we een patroon kunnen herkennen. In het eerste diagram hieronder kunnen we raden dat de relatie lineair is, en we kunnen proberen de rechte \ te vinden die het beste bij onze gegevens past (er zijn methoden om deze het beste te vinden). In het tweede diagram hieronder kunnen we raden dat de relatie kwadratisch is en opnieuw kunnen we proberen de functie \ te vinden die het beste bij de gegevens Past.
Cartesiaanse coördinaten speelden een belangrijke rol in de ontwikkeling van calculus in de tweede helft van de 17e eeuw. Calculus maakt het mogelijk om attributen van krommen uit te werken, zoals hun helling op een bepaald punt of de oppervlakte van het gebied dat tussen een kromme en de \(x\)-as ligt. Deze kunnen ook fysieke interpretaties hebben. Als we bijvoorbeeld de afstand die een auto aflegt tegen de tijd die hij heeft afgelegd, berekenen, dan geeft de helling van de resulterende curve op een gegeven moment—de snelheid waarmee de afstand ten opzichte van de tijd verandert—de snelheid weer waarmee de auto op dat moment in de tijd reed: het is de afgeleide van de functie die ons afstand geeft in termen van tijd. Zie ook Waarom zijn gradiënten belangrijk in de echte wereld?.
we kunnen ook een dimensie omhoog gaan door een derde as loodrecht op de eerste twee te overwegen, die u zich kunt voorstellen als uit uw vel papier komen en naar u wijzen. Met zo ‘ n driedimensionaal systeem kun je nu driedimensionale objecten voorstellen en visualiseren hoe een derde variabele \(z\) afhangt van je eerste twee, \(x\) en \(y\).
deze voorbeelden geven je een idee waarom coördinaten zo onmisbaar zijn geworden in alle gebieden van de wetenschap, van natuurkunde tot astronomie en engineering, en ook in de visuele industrieën om computergraphics te produceren en de computer gegenereerde beelden die we bewonderen in films en games.
In de wiskunde zelf heeft de link tussen algebra en meetkunde zijn hoogtepunt bereikt in een geheel gebied dat algebraïsche meetkunde wordt genoemd, dat een eigen fascinatie bezit. Misschien wel het meest bekende resultaat dat uit dit gebied is voortgekomen is de laatste stelling van Fermat, genoemd naar een tijdgenoot van Descartes, Pierre de Fermat, die ook een belangrijke bijdrage heeft geleverd aan de ontwikkeling van het Cartesiaanse coördinatenstelsel. Fermat overwoog een vraag die meetkunde koppelt aan de getaltheorie. Volgens de stelling van Pythagoras zijn \(a\), \(b\) en \(c\) de zijden van een rechthoekige driehoek en \(c\) de zijde tegenover de rechte hoek, dan \(a^2 + b^2 = c^2\). Er zijn oneindig veel triples van hele getallen \(a\), \(b\) en \(c\) die aan deze relatie voldoen; \((3,4,5)\) is een voorbeeld.
stel nu dat we de exponent veranderen en expressies als \ en \ en meer in het algemeen \ beschouwen waar \(n\) een natuurlijk getal groter is dan \(2\). Kunnen we nog steeds positieve hele getallen \(a\), \(b\) en \(c\) vinden die voldoen aan de vergelijking? Fermat vermoedde dat we dat niet kunnen en hij krabbelde zo veel in de marge van zijn wiskundeboek, zeggende dat hij een “prachtig bewijs” voor dat feit had die de marge te smal was om te bevatten.
dat gekrabbel zou wiskundigen meer dan 350 jaar achtervolgen. Het was pas in 1994 dat een juist bewijs van dit schijnbaar onschuldige resultaat uiteindelijk werd aangekondigd door de wiskundige Andrew Wiles. Wiles had uitgebreid gebruik gemaakt van de algebraïsche meetkunde. In het bijzonder had hij Resultaten gebruikt met betrekking tot de elliptische krommen beschreven door punten in het vlak waarvan de coördinaten voldoen aan \ Descartes’ contemplatie van een vlieg is een lange weg afgelegd!
