A step-by-step guide to building a simple chess AI

by Lauri Hartikka

laten we enkele basisconcepten verkennen die ons zullen helpen een eenvoudig schaakspel te maken AI:

Move-generation
board evaluation
MiniMax
en alpha beta snoeien.

bij elke stap verbeteren we ons algoritme met een van deze beproefde schaakprogrammeertechnieken. Ik zal laten zien hoe elk de speelstijl van het algoritme beïnvloedt.

u kunt het uiteindelijke AI-algoritme hier op GitHub bekijken.

Stap 1: Verplaats generatie en bordvisualisatie

We zullen het Schaken gebruiken.js bibliotheek voor move generatie, en schaakbord.J ‘ s voor het visualiseren van het bord. De move generation bibliotheek implementeert in principe alle regels van het Schaken. Op basis hiervan kunnen we alle juridische stappen berekenen voor een bepaalde bestuurstoestand.

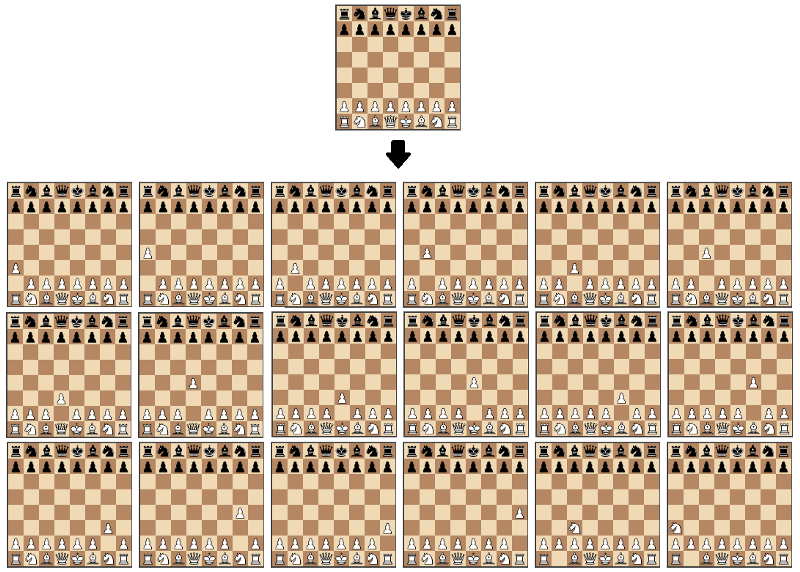
een visualisatie van de move generation functie. De startpositie wordt gebruikt als input en de output is alle mogelijke bewegingen van die positie.

het gebruik van deze bibliotheken zal ons helpen ons te concentreren op de meest interessante taak: het maken van het algoritme dat de beste zet vindt.

we beginnen met het maken van een functie die gewoon een willekeurige zet teruggeeft van alle mogelijke zetten:

hoewel dit algoritme geen zeer solide schaker is, is het een goed startpunt, omdat we er eigenlijk tegen kunnen spelen:

zwart speelt willekeurige zetten. Speelbaar op https://jsfiddle.net/lhartikk/m14epfwb/4

Stap 2 : Positie evaluatie

laten we nu proberen te begrijpen welke kant sterker is in een bepaalde positie. De eenvoudigste manier om dit te bereiken is door de relatieve sterkte van de stukken op het bord te tellen met behulp van de volgende tabel:

met de evaluatiefunctie kunnen we een algoritme maken dat de zet kiest die de hoogste evaluatie geeft:

de enige tastbare verbetering is dat ons algoritme zal nu een stuk vastleggen als het kan.

zwart speelt met behulp van de eenvoudige evaluatiefunctie. Speelbaar op https://jsfiddle.net/lhartikk/m5q6fgtb/1/

Stap 3: zoekboom met Minimax

vervolgens maken we een zoekboom waaruit het algoritme de beste zet kan kiezen. Dit wordt gedaan met behulp van de Minimax algoritme.

in dit algoritme wordt de recursieve boom van alle mogelijke bewegingen onderzocht tot een bepaalde diepte en wordt de positie geëvalueerd aan het einde van “bladeren” van de boom.

daarna keren we de kleinste of de grootste waarde van het kind terug naar de bovenliggende node, afhankelijk van of het een wit of zwart is om te verplaatsen. (Dat wil zeggen, we proberen het resultaat op elk niveau te minimaliseren of te maximaliseren.)

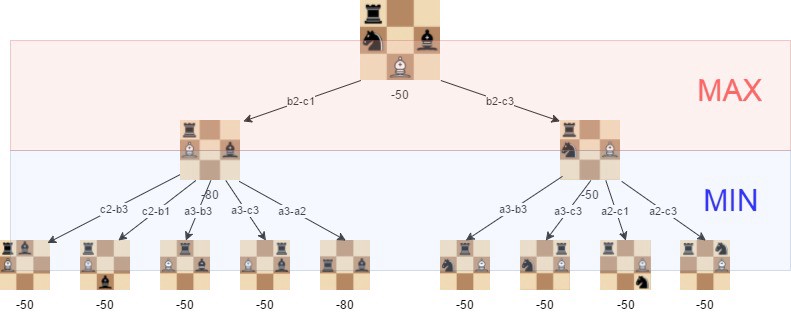
een visualisatie van het MiniMax-algoritme in een kunstmatige positie. De beste zet voor wit is b2-c3, omdat we kunnen garanderen dat we een positie kunnen bereiken waar de evaluatie -50

met minimax op zijn plaats begint ons algoritme een aantal basistactieken van Schaken te begrijpen:

Minimax met depth level 2. Speelbaar op: https://jsfiddle.net/k96eoq0q/1/

de effectiviteit van het MiniMax algoritme is sterk gebaseerd op de zoekdiepte die we kunnen bereiken. Dit is iets wat we zullen verbeteren in de volgende stap.

Stap 4: Alpha-beta snoeien

Alpha-beta snoeien is een optimalisatiemethode voor het minimax algoritme dat ons in staat stelt om enkele takken in de zoekboom te negeren. Dit helpt ons evalueren van de minimax zoekboom veel dieper, terwijl het gebruik van dezelfde middelen.

de alpha-beta snoei is gebaseerd op de situatie waarin we kunnen stoppen met het evalueren van een deel van de zoekboom als we een beweging vinden die leidt tot een slechtere situatie dan een eerder ontdekte beweging.

de alpha-beta snoei heeft geen invloed op de uitkomst van het minimax algoritme — het maakt het alleen sneller.

Het alpha-beta algoritme is ook efficiënter als we eerst die paden bezoeken die tot goede zetten leiden.

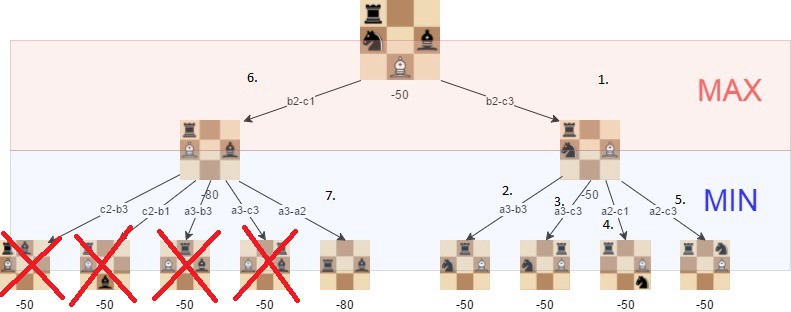
de posities die we niet hoeven te onderzoeken als alfa-beta snoeien wordt gebruikt en de boom wordt bezocht in de beschreven volgorde.

met alpha-beta, krijgen we een significante boost voor het MiniMax algoritme, zoals wordt getoond in het volgende voorbeeld:

het aantal posities dat nodig is om te evalueren als we een zoekopdracht met diepte van 4 willen uitvoeren en de” root ” positie is degene die wordt getoond.

volg deze link om de alpha-beta verbeterde versie van de chess AI te proberen.

Stap 5: verbeterde evaluatiefunctie

de initiële evaluatiefunctie is vrij naïef omdat we alleen het materiaal tellen dat op het bord wordt gevonden. Om dit te verbeteren, voegen we aan de evaluatie een factor toe die rekening houdt met de positie van de stukken. Bijvoorbeeld, een ridder op het midden van het bord is beter (omdat het meer opties heeft en dus actiever is) dan een ridder op de rand van het bord.

we gebruiken een licht aangepaste versie van vierkante tabellen die oorspronkelijk beschreven zijn in de chess-programming-wiki.

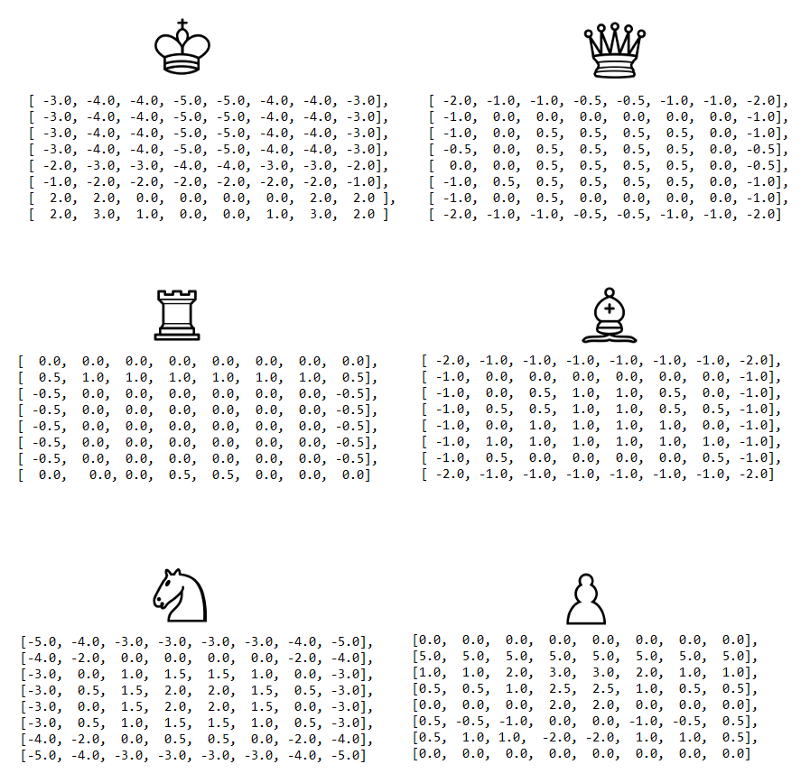
the visualized piece-square tables visualized. We kunnen verlagen of verhogen van de evaluatie, afhankelijk van de locatie van het stuk.

met de volgende verbetering beginnen we een algoritme te krijgen dat wat” fatsoenlijk”Schaken speelt, tenminste vanuit het oogpunt van een casual speler:

verbeterde evaluatie en alfa-beta snoeien met zoekdiepte van 3. Speelbaar op https://jsfiddle.net/q76uzxwe/1/

conclusies

De kracht van zelfs een eenvoudig schaakspelalgoritme is dat het geen domme fouten maakt. Dit gezegd zijnde, ontbreekt het nog steeds aan strategisch begrip.

met de methoden die ik hier heb geïntroduceerd, hebben we een schaakspel-algoritme kunnen programmeren dat basisschaak kan spelen. De “AI-deel” (Move-generatie uitgesloten) van het uiteindelijke algoritme is slechts 200 regels code, wat betekent dat de basisconcepten zijn vrij eenvoudig te implementeren. Je kunt de definitieve versie bekijken op GitHub.

enkele verdere verbeteringen die we aan het algoritme kunnen aanbrengen zijn bijvoorbeeld:

verplaatsingsvolgorde
snellere generatie van bewegingen
en eindspelspecifieke evaluatie.

KGSAU