hvordan husker du stedet på en øde øy hvor du begravet skatten din? Du velger et landemerke, sier et palme, og måler hvor mange trinn nord / sør og hvor mange trinn øst / vest du må gå fra det landemerket for å komme til skatten. Det er en enkel ide, men overraskende tok matematikere århundrer for å utvikle sitt fulle potensial på sitt eget felt. Da de endelig gjorde det, revolusjonerte det matematikk ved å samle to områder som på forsiden av det har lite å gjøre med hverandre: algebra og geometri.Når vi begynner å lære geometri, tenker vi vanligvis på enkle former som linjer, trekanter og sirkler i det todimensjonale planet. Du kan konstruere disse og mer kompliserte former ved hjelp av en linjal, kompass og vinkelmåler. De gamle Grekerne var mestere på denne type geometri: ved hjelp av bare kompasser og en rett kant (en umerket linjal) kunne de konstruere en rekke former, og de kunne til og med bevise matematiske resultater, som Pythagoras teorem, ved hjelp av disse enkle verktøyene.
det er imidlertid visse ting du ikke kan gjøre ved hjelp av disse grunnleggende metodene. To former, si en linje og en sirkel, kan eller ikke krysser, og de kan krysse på forskjellige måter: kanskje linjen bare berører sirkelen, kanskje den barberer en liten bue av den, eller kanskje den kutter den i halvparten. For å registrere denne informasjonen trenger du en måte å beskrive plasseringen av figurene.
dette er hvor treasure island ideen kommer til nytte. Det illustrerer det Som kalles Det Kartesiske koordinatsystemet. Velg et punkt i flyet, kalt opprinnelsen, og trekk to vinkelrette akser gjennom den, en horisontal og en vertikal. Ethvert punkt i flyet kan nås fra opprinnelsen ved å reise en viss avstand \(x\) langs den horisontale aksen og en viss avstand \(y\) langs den vertikale aksen. Tallene \((x, y)\) er koordinatene til punktet. Opprinnelsen selv har koordinater \(((0,0)\). Den delen av den horisontale aksen (også kalt \(x\)-aksen) som ligger til venstre for opprinnelsen og delen av den vertikale aksen (\(y\)-aksen) under opprinnelsen er beskrevet av negative tall.
Kartesiske koordinater er oppkalt etter den franske filosofen Og matematikeren René Descartes fra det 17.århundre. Det er en (sannsynligvis usann) historie At Descartes oppfant disse koordinatene mens han lå i sengen og så på en flue i taket og lurte på hvordan man skal beskrive beliggenheten. Descartes ‘ forkjærlighet for å ligge i sengen til middag kan faktisk ha vært årsaken til hans død, som skjedde I Stockholm i 1650. Descartes var I Sverige for å fungere som matematikklærer Til Dronning Christina, som dessverre foretrukket å jobbe tidlig om morgenen. Ifølge noen rapporter var det disse tidlige timene og De Skandinaviske temperaturene som forårsaket lungebetennelsen som til slutt drepte ham. Andre har antydet at Han ble forgiftet av En Katolsk prest som var bekymret For Descartes ‘ radikale teologi.uansett Er Det Kartesiske koordinatsystemet en Av Descartes viktigste legater (selv om han ikke var den eneste personen som hadde ideen). Det tillater oss å svare på geometriske problemer ved hjelp av algebra og å visualisere algebraiske relasjoner som ellers ville forbli ganske abstrakte. Ta for eksempel ligningen \ Vi kan plotte grafen til denne funksjonen i Et Kartesisk koordinatsystem ved å plotte alle punkter hvis koordinater er av skjemaet \((x, 2x-1)\): poeng som \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), og \((1.73, 2.46)\). I dette tilfellet er grafen en rett linje som møter \(y\)-aksen ved punktet \(((0, -1)\) og har en helling på \(2\).
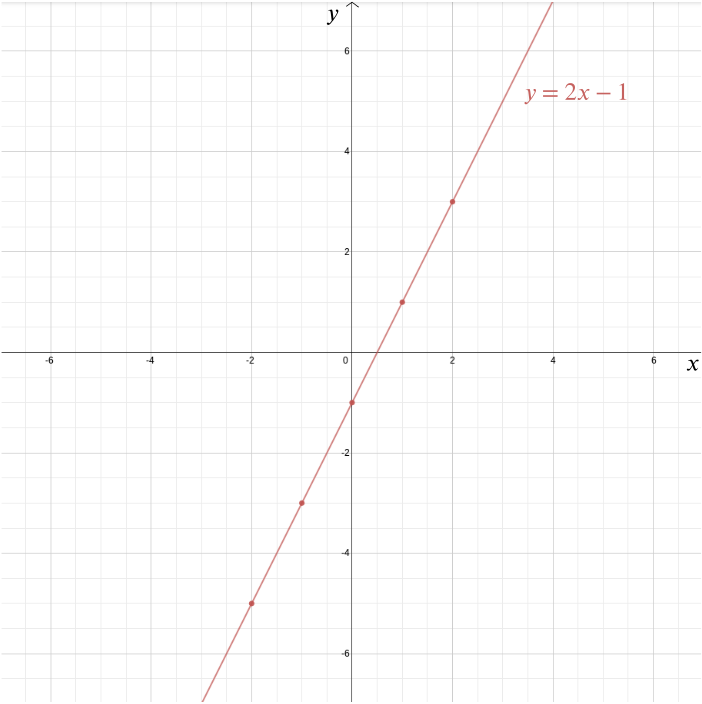
mer generelt er hver rett linje gitt av en ligning av formen \ hvor \ (m\) gir deg hellingen til linjen og \((0, b)\) er punktet der den krysser\(y\)-aksen. En vertikal linje som ikke krysser\(y\)-aksen er gitt ved en ligning av formen \(x=c\). I dette tilfellet er \((c, 0)\) punktet der det krysser \(x\)-aksen.
hva med en sirkel? En sirkel består av alle de punktene som ligger på lik avstand \(r\) fra et gitt punkt \(m\). La oss anta at \(m\) er punktet \(((0,0)\). Fra Pythagoras teorem vet vi at hvis et punkt \((x, y)\) ligger i avstand \(r\) fra \(((0,0)\), så \
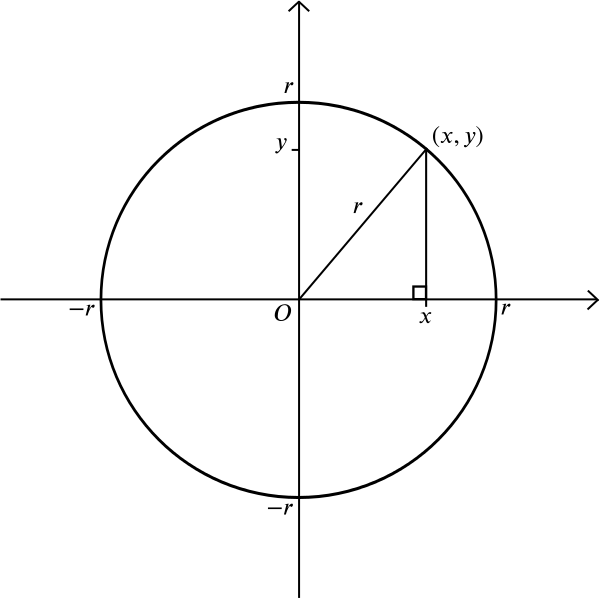
dette er derfor ligningen for en sirkel av radius \(r\) sentrert på opprinnelsen. Du kan trene for deg selv at en sirkel med radius \(r\) sentrert på punktet \((a,b)\) har ligningen \ Men her er et mer komplisert spørsmål: hvilken form får du når du vurderer alle punkter som ligger på like avstand fra et gitt punkt og en gitt linje? Uten et koordinatsystem kan du tegne punktet og linjen og eksperimentere med linjalen eller kompassene. Du kan tegne noen få poeng som ligger like langt fra begge og se om du kan gjette den generelle formen.
Bevæpnet med et koordinatsystem, men svaret blir mye enklere og mye mer presis. Anta at det gitte punktet er i avstand \(1\) fra den oppgitte linjen. La oss plassere det gitte punktet ved opprinnelsen og den gitte linjen slik at den er horisontal, gitt av ligningen \ Ved Pythagoras teorem avstanden til et hvilket som helst punkt\ ((x,y)\) fra \ (((0,0)\) er \(\sqrt{x^2 + y^2}\). Avstanden fra et punkt \((x, y)\) til linjen \(y = -1\) er \(|y+1/\) (vi bruker absoluttverdien her fordi \(y\)-koordinaten kan være negativ). Hvis de to er like, gir \ Kvadrering begge sider \ Omarrangering gir \ så et punkt på like avstand fra punktet \((0,0)\) og linjen \(y=-1\) har koordinater \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Du kan selv sjekke at det omvendte også er sant: hvert punkt med disse koordinatene ligger i like avstand fra punktet \((0,0)\) og linjen \(y=-1\).
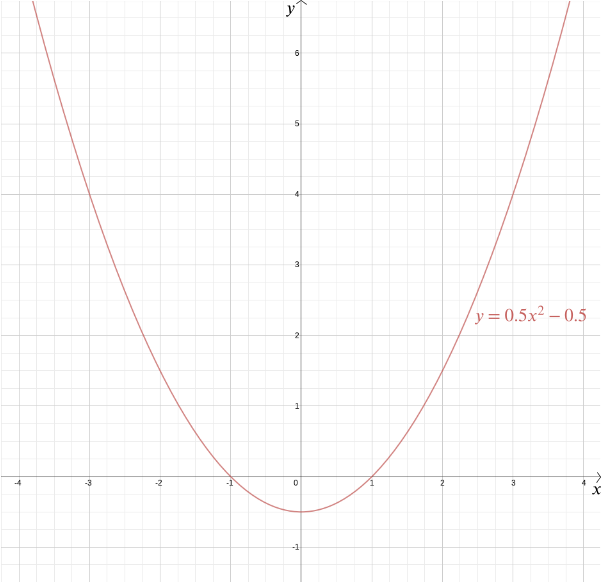
vi kan plotte grafen til denne funksjonen for å se ønsket form, som viser seg å være en parabola. Faktisk gir hver kvadratisk funksjon \ for \(a\), \(b\) og \(c\) konstanter oss en parabola. Denne kjente formen, som kan komme i så mange subtile variasjoner-lang og tynn eller knebøy og flat-er fanget av dette praktiske algebraiske uttrykket. Det faktum at begrepene «kvadratisk funksjon» og «parabola» i dag nesten betraktes som synonymt, fremhever hvor vellykket Descartes ‘ ide har vært. Mer generelt gir et algebraisk forhold mellom to variabler \(x\) og\ (y\) oss en kurve som vi kan plotte ved Hjelp Av Kartesiske koordinater.
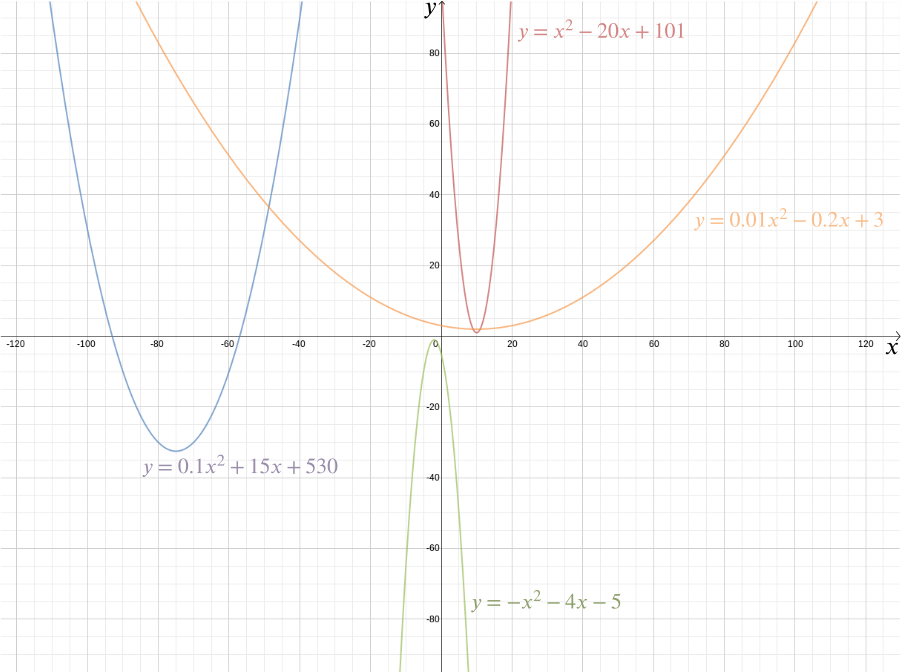
den algebraiske representasjonen gjør det enkelt å svare på en rekke geometriske spørsmål. For å utarbeide skjæringspunktene for linjen gitt av \ og parabolen \(y = \frac{x^2}{2} – \frac{1}{2}\), merker vi bare at\ (y\) koordinaten til et hvilket som helst punkt \((x,y)\) ligger på begge må tilfredsstille begge ligningene, så \ Dette gir \ Løse den kvadratiske ligningen vi får \ og \ så skjæringspunktene er på \
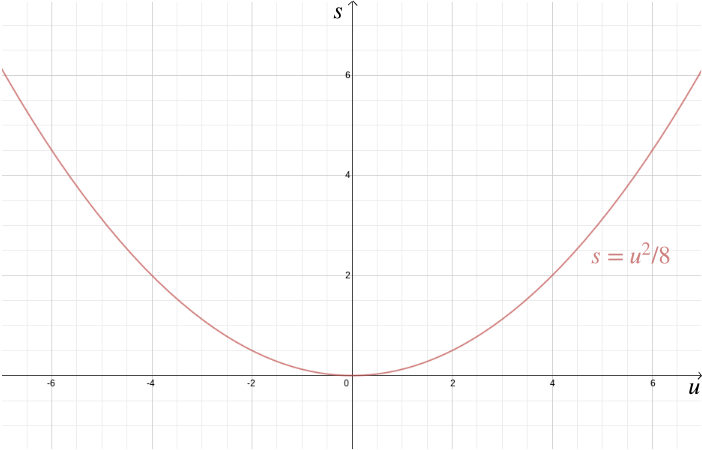
Bortsett fra å løse geometriske problemer, Hjelper Kartesiske koordinater også med å visualisere algebraiske relasjoner. Anta for eksempel at en bil kjører med fart \(u\) og føreren bruker bremsene, noe som resulterer i en konstant retardasjon på for eksempel \(-4\) meter / sekunder\(^2\). Stoppavstanden \(s\) – avstanden bilen dekker før den stopper – er gitt av det algebraiske forholdet \ Plotting dette ved Hjelp Av Kartesiske koordinater bringer hjem hvor viktig det er å bremse i byområder, fordi stoppavstanden øker raskt med \(u\).
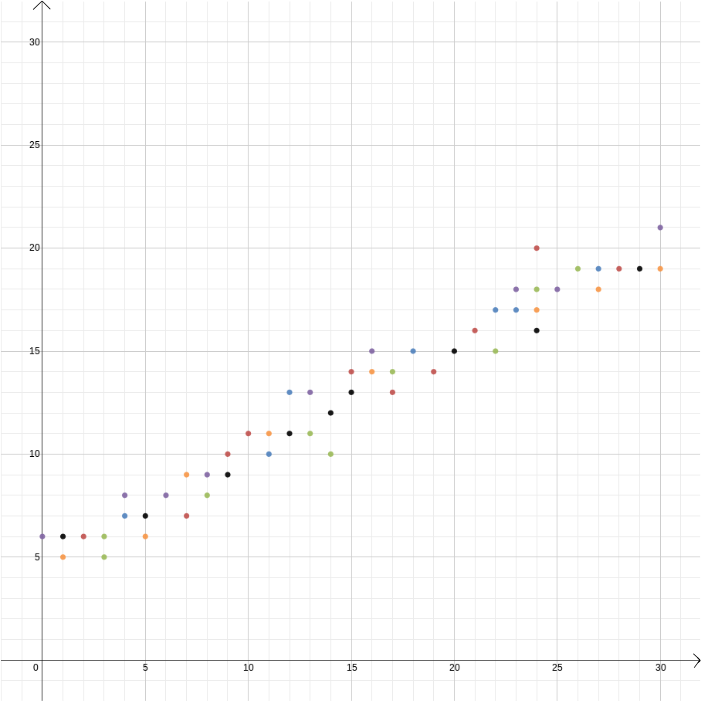
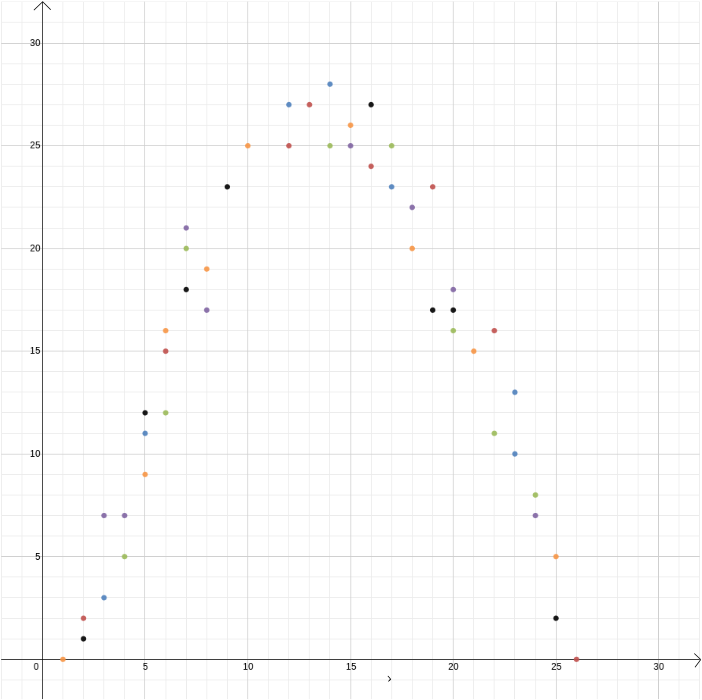
i dette eksemplet kjente vi forholdet mellom to variabler fordi det kan utledes av fysikkens lover. Men Kartesiske koordinater er også nyttige når du mistenker at to variabler er relaterte, men du vet ikke hvordan. Anta at vi tror at det er et forhold mellom fortjenesten fra en iskremselger og utetemperaturen. For å finne ut hva det forholdet kan være, kan vi måle temperatur og fortjeneste over, si i løpet av et år og plotte verdiene mot hverandre, med temperatur registrert på\(x\)-aksen og fortjeneste på \ (y\) – aksen. Vi kan da se om vi kan se et mønster. I det første diagrammet nedenfor kan vi gjette at forholdet er lineært, og vi kan prøve å finne den rette linjen \ som passer best til våre data (det finnes metoder for å finne dette som passer best). I det andre diagrammet nedenfor kan vi gjette at forholdet er kvadratisk og igjen kan vi prøve å finne funksjonen \ som passer best til dataene.
Kartesiske koordinater spilte en viktig rolle i utviklingen av kalkulus i andre halvdel av det 17.århundre. Kalkulus gjør det mulig å trene attributter av kurver som deres helling på et gitt punkt eller området i regionen som ligger mellom en kurve og \(x\)-aksen. Disse kan også ha fysiske tolkninger. For eksempel, hvis vi plotter avstanden en bil reiser mot tiden den har vært på reise, helningen av den resulterende kurven på et gitt tidspunkt—frekvensen av endring av avstand i forhold til tid—representerer hastigheten som bilen var på reise på det øyeblikket i tid: det er den deriverte av funksjonen som gir oss avstand i form av tid. Se også Hvorfor er gradienter viktige i den virkelige verden?.
Vi kan også gå opp en dimensjon ved å vurdere en tredje akse vinkelrett på de to første, som du kan forestille deg som kommer ut av arket ditt og peker på deg. Ved å bruke et slikt tredimensjonalt system kan du nå representere tredimensjonale objekter og visualisere hvordan en tredje variabel\ (z\) avhenger av de to første, \(x\) og \ (y\).disse eksemplene skal gi deg en følelse av hvorfor koordinater har blitt så uunnværlige på alle områder av vitenskap, fra fysikk til astronomi og ingeniørfag, og også i visuelle næringer for å produsere datagrafikk og datagenererte bilder vi beundrer i filmer og spill.i matematikken har sammenhengen mellom algebra og geometri kulminert i et helt område kalt algebraisk geometri, som har en egen fascinasjon. Kanskje det mest kjente resultatet som har kommet fra dette området er Fermats Siste Teorem, oppkalt etter En samtid Av Descartes, Pierre De Fermat, som også bidro betydelig til utviklingen av Det Kartesiske koordinatsystemet. Fermat vurderte et spørsmål som knytter geometri til tallteori. Ifølge Pythagoras teorem, hvis \(a\), \(b\) og \(c\) er sidene av en rettvinklet trekant og \(c\) er siden motsatt den rette vinkelen, så \(a^2 + b^2 = c^2\). Det er uendelig mange tripler av hele tall \(a\), \(b\) og \(c\) som tilfredsstiller dette forholdet; \((3,4,5)\) er et eksempel.anta nå at vi endrer eksponenten og vurderer uttrykk som \ og \ og mer generelt \ hvor \(n\) er et naturlig tall større enn \(2\). Kan vi fortsatt finne positive hele tall \(a\), \ (b\) og\ (c\) som tilfredsstiller ligningen? Fermat mistenkte at vi ikke kan, og han skriblet så mye i margen av sin matte lærebok, sier han hadde en «fantastisk bevis» for det faktum som marginen var for smal til å inneholde.
den skriblingen skulle hjemsøke matematikere i over 350 år. Det var ikke før 1994 at et korrekt bevis på dette tilsynelatende uskyldige resultatet endelig ble annonsert av matematikeren Andrew Wiles. Wiles hadde gjort utstrakt bruk av algebraisk geometri. Spesielt hadde han brukt resultater om elliptiske kurver beskrevet av punkter i flyet hvis koordinater tilfredsstiller \ Descartes ‘ kontemplasjon av en fly har kommet langt!
