Ces@ro summering

admin

det er mer enn en måte å summere en uendelig serie på. Cesà summering lar deg beregne summen av serier som ikke har en sum i klassisk forstand.

Anta at vi har en uendelig serie

a_0 + a_1 + a_2 + \cdots

den nte delvise summen av serien er gitt av

S_n = \sum_{i=0}^n a_i p den klassiske summen av serien, hvis den eksisterer, er definert til å være grensen for dens delvise summer. Det vil si,

\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\til\infty} \sum_{i=0}^n a_i

Cesà summering tar en annen tilnærming. I stedet for å ta grensen for delbeløpene, tar den grensen for gjennomsnittet av delbeløpene. For å være spesifikk, definer

C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}

og definer Ces@ro summasjonen til å være grensen For Cn som n går til uendelig. Hvis en serie har en sum i klassisk forstand, har den også en sum I Cesà forstand, og grensene er de samme. Men noen serier har En Ces5uro sum som ikke har en klassisk sum. Eller kanskje begge grensene eksisterer, men de mellomliggende trinnene I Cesà summering er bedre opptatt, som vi ser i et eksempel nedenfor.

hvis Du uttrykker Cn i form av de opprinnelige an-begrepene, får du

C_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i

med andre ord, Er Den Nte Ces@ro delvise summen en reweighting av de klassiske delvise summene, med vektene som endres som en funksjon av n. Merk at for faste I, fraksjonen multiplisere ai går til 1 som n øker.

Fej Hryvnias summering og Gibbs fenomen

Fej Hryvnias summering er Cesàro summering brukt på Fourierrekker. De (vanlige) partielle summene av En Fourier-serie gir den beste tilnærmingen til en funksjon målt ved minste kvadraters norm. Men Ces ④ro delbeløpene kan være kvalitativt mer som funksjonen blir tilnærmet. Vi demonstrerer dette nedenfor med en firkantbølge.

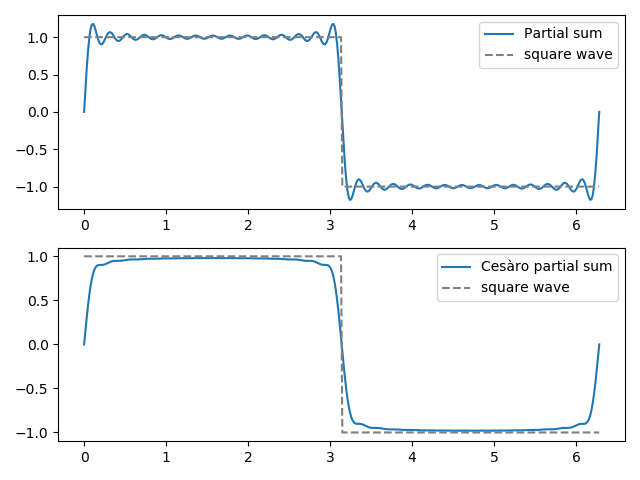
den 30. ordinære delvise summen viser Begynnelsen På Gibbs-fenomenet, «flaggermusørene» øverst på firkantbølgen og deres speilbilde nederst. Den 30. Cesà delvis summen er jevnere og eliminerer Gibbs fenomener nær diskontinuiteten i kvadratbølgen.

flere Innlegg I Fourier-serien

  • Fourier-bessel-serien
  • Moteksempel På Dirichlet-prinsippet
  • Klippet sinusbølger

Legg igjen en kommentar

Din e-postadresse vil ikke bli publisert.