無限級数を合計する方法は複数あります。 Cesàro総和を使用すると、古典的な意味での合計を持たない系列の合計を計算できます。私たちは無限級数を持っていると仮定します
シリーズのn番目の部分和はで与えられます
古典的な級数の和は、もし存在するならば、その部分和の極限として定義される。 つまり、
Cesàro総和は異なるアプローチを取ります。 部分合計の限界を取るのではなく、部分合計の平均の限界を取る。 具体的には、C_N=\frac{S_0+S_1+s_2+\ldots+S_N}{n}
を定義し、Nが無限大になるときのCesàro総和をCnの限界と定義します。 級数が古典的な意味で和を持つならば、それはまたCesàroの意味で和を持ち、そして極限は同じである。 しかし、いくつかの級数は、古典的な和を持たないチェザロ和を持っています。 あるいは、両方の限界が存在するかもしれませんが、Cesàro総和の中間ステップは、以下の例で見るように、より良い動作をします。P>
元の項でCnを表現すると、C_N=\sum_{i=0}^n\frac{n-i+1}{n+1}a_i
言い換えれば、n番目のCesàro部分和は、重みがnの関数として変化する古典的な部分和の重み付けです。aiはnが増加するにつれて1になります。
フェジェール総和とギブス現象
フェジェール総和は、フーリエ級数に適用されるCesàro総和です。 フーリエ級数の(通常の)部分和は、最小二乗ノルムによって測定される関数に最良の近似を与える。 しかし、Cesàro部分和は、定性的には近似されている関数のようなものかもしれません。 以下では、方形波でこれを示します。
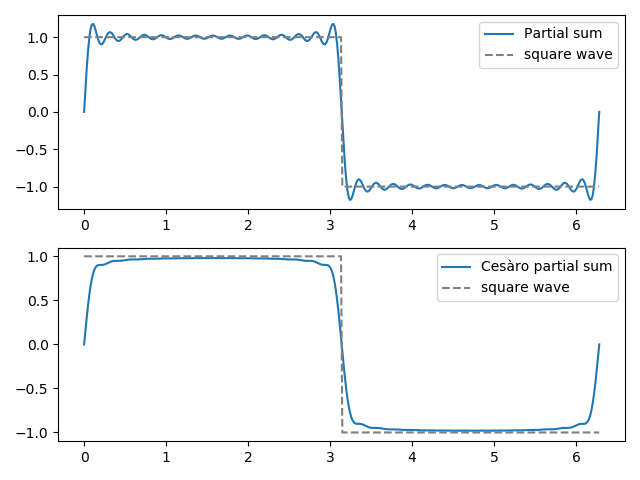
30番目の通常の部分和は、ギブス現象の始まり、方形波の上部にある”コウモリの耳”、下部にある鏡像を示しています。 30番目のCesàro部分和はより滑らかであり、方形波の不連続性の近くのGibbs現象を排除する。
より多くのフーリエ級数の投稿
- フーリエ-ベッセル級数
- ディリクレの原理への反例
- クリッピング正弦波
