どのようにあなたはあなたの宝物を埋めた無人島のスポットを覚えていますか? あなたは、ランドマークを選択し、ヤシの木を言うと、どのように多くのステップ北/南とどのように多くのステップ東/西あなたは宝物に到達するために、そのランドマークから行かなければならない測定します。 それは簡単なアイデアですが、驚くべきことに、数学者は自分の分野でその可能性を最大限に発揮するために何世紀もかかりました。 彼らが最終的にやったとき、それはお互いにほとんど関係のない2つの領域をまとめることによって数学に革命をもたらしました:代数と幾何学。
幾何学の学習を始めるとき、私たちは通常、二次元平面内の線、三角形、円のような単純な形状を考えます。 定規、コンパス、分度器を使用して、これらの複雑な形状を構築することができます。 古代ギリシャ人は、幾何学のこのタイプのマスターだった: ちょうどコンパスと直線エッジ(マークされていない定規)を使用して、彼らは形状の範囲を構築することができたし、彼らも、これらの単純なツールを使用して、ピタゴラスの定理のような数学的な結果を、証明することができました。しかし、これらの基本的な方法を使用して行うことはできません。
しかし、いくつかのことがあります。 線と円の2つの図形が交差している場合と交差していない場合があり、それらはさまざまな方法で交差する可能性があります:おそらく線は円に この情報を記録するには、図形の位置を記述する方法が必要です。
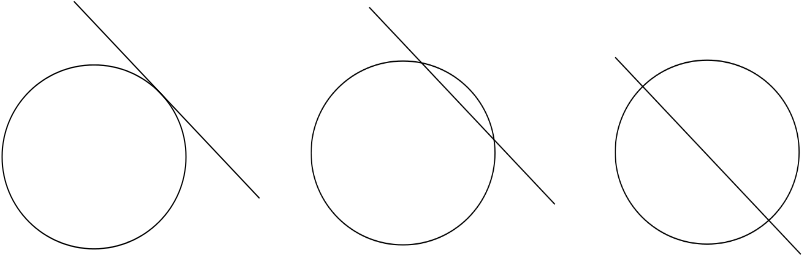
これは宝島のアイデアが役に立つ場所です。 これは、デカルト座標系と呼ばれるものを示しています。 原点と呼ばれる平面上の点を選択し、それを介して水平軸と垂直軸の2つの垂直軸を描画します。 平面上の任意の点は、水平軸に沿って一定の距離\(x\)を移動し、垂直軸に沿って一定の距離\(y\)を移動することによって原点から到達することができます。 数字\((x,y)\)は点の座標です。 原点自体は座標\((0,0)\)を持ちます。 原点の左にある水平軸の部分(\(x\)軸とも呼ばれます)と、原点の下にある垂直軸の部分(\(y\)軸)は負の数で記述されます。\(x\)軸は、\(x\)軸とも呼ばれます。\(x\)軸は、\(x\)軸とも呼ばれます。\(x\)軸は、\(x\)軸
デカルト座標は、17世紀のフランスの哲学者で数学者のルネ-デカルトにちなんで命名されました。 天井のハエを見てベッドに横たわって、その位置を記述する方法を疑問に思っている間に、デカルトがこれらの座標を発明した(おそらく真実ではない)話があります。 正午までベッドに横たわっているためのデカルトの傾向は、実際には1650年にストックホルムで発生した彼の死の原因であった可能性があります。 デカルトはスウェーデンにいて、残念ながら朝早く仕事をすることを好んだクリスティーナ女王の数学の家庭教師として働いていました。 いくつかの報告によると、最終的に彼を殺した肺炎を引き起こしたのは、これらの初期の時間とスカンジナビアの気温でした。 他の人たちは、デカルトの急進的神学を心配していたカトリックの司祭によって毒殺されたと示唆している。
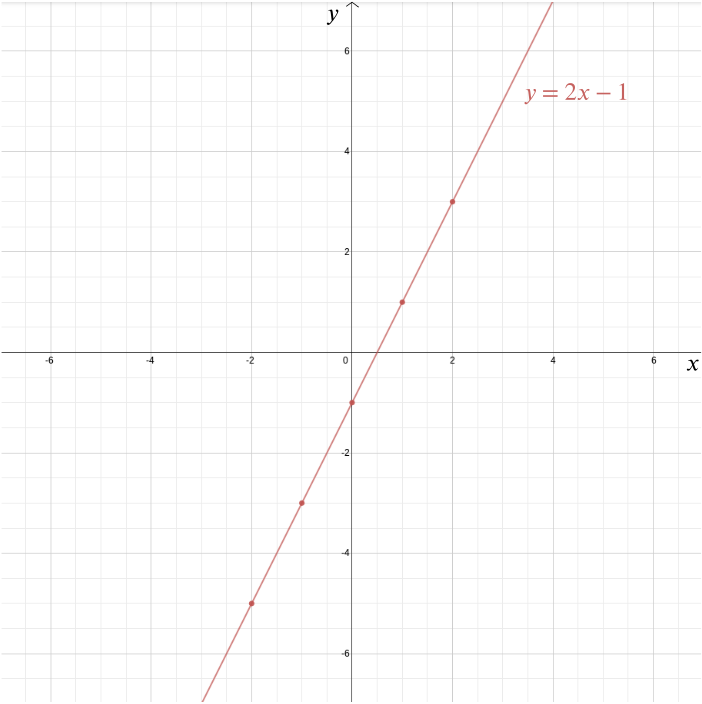
いずれにせよ、デカルト座標系はデカルトの最も重要な遺産の一つです(彼はアイデアを持っている唯一の人ではありませんでしたが)。 それは代数を使って幾何学的問題に答え、そうでなければ非常に抽象的なままである代数的関係を視覚化することを可能にする。 たとえば、座標が\((x,2x-1)\)の形式のすべての点をプロットすることによって、この関数のグラフをデカルト座標系でプロットすることができます。: などのポイント\((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), と\((1.73, 2.46)\). この場合、グラフは点\((0,-1)\)で\(y\)軸を満たし、勾配が\(2\)の直線です。p>
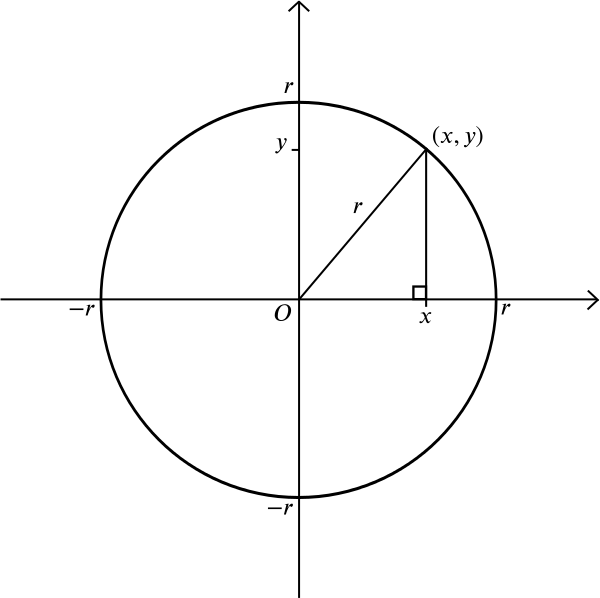
円は、与えられた点\(m\)から等しい距離\(r\)にあるすべての点で構成されます。 \(M\)が点\((0,0)\)であるとしましょう。 ピタゴラスの定理から、点\((x,y)\)が\((0,0)\)から\(r\)の距離にある場合、\(p>
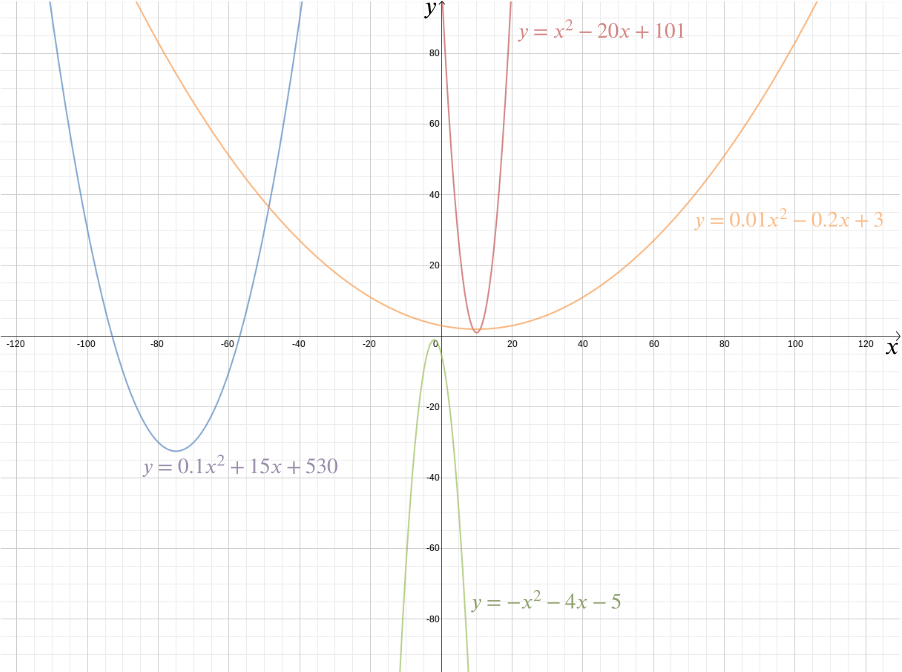
この関数のグラフをプロットして、放物線であることが判明した必要な形状を見ることができます。 実際、\(a\)、\(b\)、\(c\)定数のすべての二次関数\は放物線を与えます。 長くて薄い、またはスクワットとフラット——非常に多くの微妙なバリエーションで来ることができるこのおなじみの形状は、この便利な代数式によっ 今日、”二次関数”と”放物線”という用語がほぼ同義と考えられているという事実は、デカルトのアイデアがどれほど成功したかを強調しています。 より一般的には、2つの変数\(x\)と\(y\)の間の任意の代数的関係は、デカルト座標を使用してプロットできる曲線を与えます。\(x\)と\(y\)の間の任意の代数的関係は、
代数表現は、幾何学的な質問の全範囲に答えることが容易になります。 \で与えられた線と放物線\(y=\frac{x^2}{2}-\frac{1}{2}\)の交点を計算するには、両方の上にある任意の点\((x,y)\)の\(y\)座標が両方の方程式を満たさなければならないことに注意してください。\これは\と\を得る二次方程式を解くことを与えるので、交点は\
にあります幾何学的問題を解くこととは別に、デカルト座標も代数的関係を視覚化するのに役立ちます。 たとえば、自動車が速度\(u\)で走行していて、運転者がブレーキをかけていると仮定すると、たとえば\(-4\)メートル/秒\(.2\)の一定の減速が得られます。 停止距離\(s\)—車が停止する前にカバーする距離-代数関係によって与えられる\これをデカルト座標を用いてプロットすることは、停止距離が\(u\)とともに急速に増加するため、都市部で減速することがいかに重要であるかをもたらす。p>
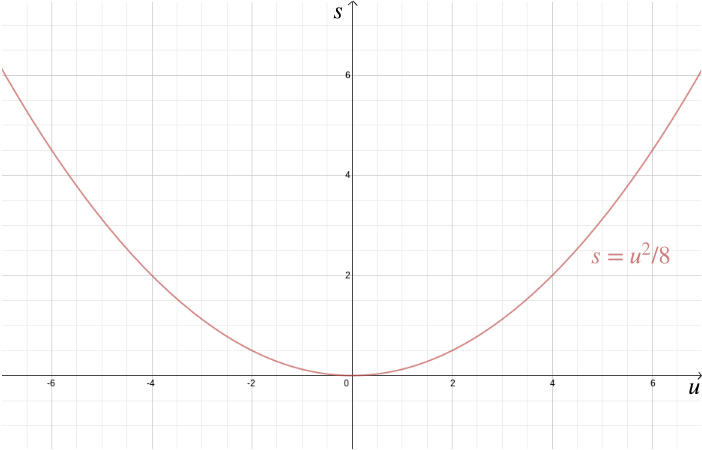
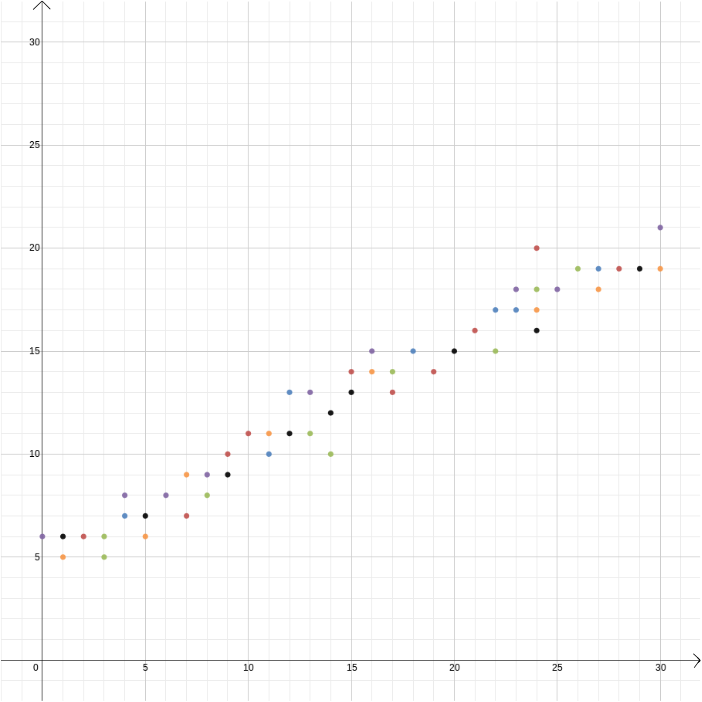
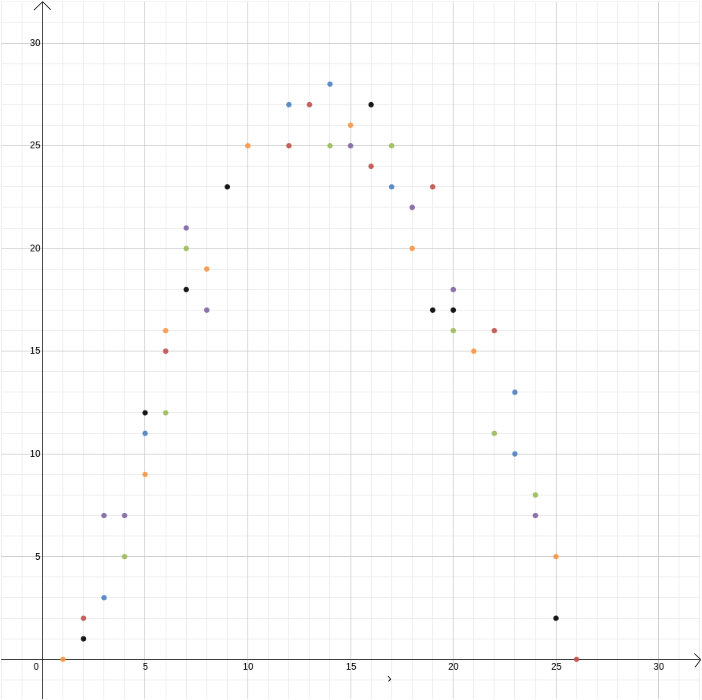
この例では、物理法則から導出できるため、二つの変数間の関係を知っていました。 しかし、デカルト座標は、2つの変数が関連していると思われるが、その方法がわからない場合にも便利です。 アイスクリーム販売者の利益と外気温との間には関係があると考えてみましょう。 その関係が何であるかを知るために、温度を測定し、1年の経過を超えて利益を得て、温度を\(x\)軸に記録し、利益を\(y\)軸に記録して、値を互いにプロットすることができます。 次に、パターンを見つけることができるかどうかを確認できます。 下の最初の図では、関係が線形であると推測し、データに最も適した直線\を見つけることができます(この最適な近似を見つける方法があります)。 下の2番目の図では、関係が2次であると推測するかもしれませんし、データに最も適した関数\を見つけようとすることもできます。
デカルト座標は、17世紀後半の微積分の開発に大きな役割を果たしました。 微積分学は、与えられた点での傾きや曲線と\(x\)軸の間にある領域の面積などの曲線の属性を計算することを可能にします。\(x\)軸と\(x\)軸との間にある領域の面積を計算することを可能にします。\(x\) これらは、あまりにも物理的な解釈を持つことができます。 たとえば、車が移動している時間に対して移動する距離をプロットすると、与えられた時間における結果の曲線の傾き—時間に対する距離の変化率—は、車がその瞬間に移動していた速度を表します。 また、現実世界で勾配が重要な理由を参照してください。.
また、最初の二つに垂直な第三の軸を考慮することによって次元を上げることができます。 このような3次元システムを使用すると、3次元オブジェクトを表現し、3番目の変数\(z\)が最初の2つ、\(x\)と\(y\)にどのように依存するかを視覚化でき
これらの例は、物理学から天文学、工学に至るまで、科学のすべての分野で座標が非常に不可欠になった理由をいくつかの感覚を与える必要があり、また、コンピュータグラフィックスと私たちが映画やゲームで賞賛するコンピュータ生成された画像を生成するための視覚産業でもあります。数学自体では、代数と幾何学の間のリンクは、それ自身の魅力を保持している代数幾何学と呼ばれる全体の領域で最高潮に達しています。
数学自体では、代数と幾何学の間のリンクは、それ自身の魅力を保持しています。 おそらく、この分野から浮上している最も有名な結果は、デカルト座標系の開発にも大きく貢献したデカルトの同時代のピエール-ド-フェルマーにちなんで命名されたフェルマーの最終定理である。 フェルマーは幾何学を数論に結びつける問題を検討していた。 ピタゴラスの定理によれば、\(a\)、\(b\)、\(c\)を直角三角形の辺とし、\(c\)を直角の反対側とすると、\(a^2+b^2=c^2\)となる。 この関係を満たす整数\(a\)、\(b\)、\(c\)の無限に多くのトリプルがあります; \((3,4,5)\)は一例です。ここで、指数を変更し、\and\、そしてより一般的には\(n\)が\(2\)より大きい自然数であるような式を考えるとします。\(n\)が\(n\)より大きい場合、\(n\)は\(n\)より大きい 我々はまだ方程式を満たす正の整数\(a\)、\(b\)、\(c\)を見つけることができますか? フェルマーは、私たちができないと疑われ、彼は彼の数学のテキストブックのマージンに同じくらい走り書きし、マージンが狭すぎるという事実のために”素晴らその落書きは350年以上にわたって数学者を悩ませることでした。
この一見無害な結果の正しい証明が数学者Andrew Wilesによって最終的に発表されたのは1994年までではありませんでした。 ワイルズは代数幾何学の広範な使用をしていた。 特に、彼は座標が\デカルトのフライの熟考を満たす平面上の点によって記述された楕円曲線に関する結果を使用していた長い道のりを歩んできた!
