これをやってみましょう。 私は直角三角形の重心の式を導出するつもりです。 どうして?Div>
見て、私たちは楽しみを持っているつもりです。 私はすでにヨーダのミームを含めてきました。 何が間違って行くことができますか?ここに三角形があります。
ここに三角形があります。
/div>
、通常の青い三角形のように見えます。 だろ? しかし、これはMの質量を持ついくつかの薄い金属板であると仮定します。 重心の基本的な定義から始めましょう。
これは基本的に加重平均です。 わかりました、それは加重平均です。 しかし、オブジェクトを小さな断片の束に分割する場合は、各質量のベクトル位置とその小さな質量を掛けます。 次に、すべてを加算し、総質量で除算します。 それが質量の中心です。 これは別の写真です。/div>もちろん、この場合、私たちは作品の束を持っていません。 私たちは連続的な質量を持っています。 それは、代わりに和を積分に変えることができることを意味します。 同時にx方向とy方向の両方を扱う代わりに、私はちょうどy重心を考慮するつもりです。私はこの三角形を水平の長方形の束に分割することから始めます。
私はこの三角形を水平の長方形の束に分割することから始めます。 ここにそれらの長方形の1つがあります。/div>私はこれらの細い長方形を使って重心を見つけることができます。 私はちょうど各長方形の位置と各長方形の質量を乗算する必要があります。 位置はかなり簡単です、それは”y”です。 質量はもう少しトリッキーです。 また、三角形を上に移動する長方形の場合、それらはより小さな質量でより小さくなることに注意してください。この小さな長方形の面積は、その面積に比例する必要があります。
この小さな長方形の面積は、その面積に比例する必要があります。 三角形全体の面積密度を次のように定義しましょう。


つまり、小さな四角形の質量は、その面積に依存する小さな値(dm)になります。Div>
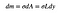
最後に、私はの面でLを取得する必要があります私は最初にxの観点から式を取得することによってそれを行います。 長方形の左側を「x」、右側を「s」と呼ぶことができます。 これは、次のことを意味します。

しかし、その三角形の左側式を持つ行として記述することができます:
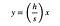

どのように迅速なリアリティチェック あまりにも遠くになる前に物事が機能していることを確認しましょう。 Y=hとするとどうなりますか? これは、長方形の長さがゼロの三角形の上部にある必要があります。 うん。 それは動作します。 Y=0はどうですか? 長方形の長さはsにする必要があります。今、私はちょうどこのすべてのものを一緒に置く必要があります。
これは、長方形のスライスの質量です。
“s”はFTW(勝利のために)。
それは今のところ十分です。 次のステップは、質量のy中心の式を書くことです。 私はこの部分の幅をゼロにするつもりなので、私は和の代わりに積分を得るつもりです。/div>私はこれを統合することができますが、私はそれを二つの部分に分割すると簡単です。 代数のほんの少しは私を与える:

制限で評価する(下限がゼロであるため簡単です):
ブーム。 それは質量のy中心です。 それは距離の単位を持っています(それはすべきです)。 また、y中心の質量は、x方向の三角形の長さ(パラメータs)に依存しないことに注意してください。 それはクールです。 また、質量のx中心を簡単に見つけることができることを意味します。 私がする必要があるのは、同じ三角形を垂直の長方形に分割することだけです。/div>数学をx方向で同じにするには、原点を三角形の他の角に移動する必要があります。 これは、質量のx中心が右側から(1/3)sであることを意味します。 これは、質量の総中心を与えます:

クール。
質量中心の数値計算
ああ、あなたは私が終わったと思ったのですか? まだ終わってない どのようにこれはどうですか—質量中心の数値計算? はい、それは楽しいでしょう。 ここに私の計画があります。
- 三角形の実際の寸法を選択します。 私は変数で数値計算を行うことはできません。 番号が必要だ 私はs=4、h=1を使うつもりです。 はい、ユニットがあるはずですが、それは問題ではありません。 OK、面積密度は1です(それも重要ではないことは明らかです)。
- 小さなステップサイズを選択します。 私は0.01×0.01のサイズの小さなブロックを持っているとしましょう。 このブロックとその質量のベクトル位置を求めます(すべてのブロックの質量は同じです)。
- 質量の中心の和の公式バージョンを使用します。
- 三角形のすべての部分が覆われるまでブロックを移動します。
これをしましょう。 わかりました、小さい難しさがあります。 私はループの中でループを行う必要があります。 外側のループは、これらの水平行を0からhに移動します。
ここにコードの主要部分があります(ここでは完全なコード):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
ピースサイズが0.01×0.01で、私は次のようになります:

うん、私はそれにかなり満足しています。
