Facciamo questo. Ho intenzione di ricavare l’espressione per il centro di massa per un triangolo rettangolo. Perché?

Vedi, stiamo andando a divertirsi. Ho già incluso un meme Yoda. Cosa potrebbe andare storto?

Ecco il triangolo.

Oh, si presenta come un normale triangolo blu. Giusto? Ma supponiamo che questa sia una sottile lamiera con una massa di M. Come troveresti la posizione del centro di massa? Iniziamo con la definizione di base di centro di massa.

Questo è essenzialmente una media ponderata. OK, è una media ponderata. Ma se rompi l’oggetto in un mucchio di piccoli pezzi, moltiplica la posizione vettoriale di ogni massa e la sua piccola massa. Quindi aggiungi tutto e dividi per la massa totale. Quello è il centro di massa. Ecco un’altra foto.

Naturalmente in questo caso non abbiamo un mucchio di pezzi. Abbiamo una massa continua. Ciò significa che possiamo invece trasformare la somma in un integrale. Invece di occuparmi contemporaneamente di entrambe le direzioni x e y, considererò solo il centro di massa y.

Inizierò rompendo questo triangolo in un gruppo di rettangoli orizzontali. Ecco uno di quei rettangoli.

Così, Posso usare queste skinny rettangoli per trovare il centro di massa. Ho solo bisogno di moltiplicare la posizione di ogni rettangolo e la massa di ogni rettangolo. La posizione è piuttosto semplice, è “y”. La massa è un po ‘ più difficile. Inoltre, si noti che per i rettangoli che si muovono verso l’alto del triangolo, sono più piccoli con massa più piccola.

L’area di questo piccolo rettangolo dovrebbe essere proporzionale alla sua area. Mi permetta di definire l’area di densità per l’intero triangolo:

questo significa Che la massa di un piccolo rettangolo sarà il piccolo valore (dm) che dipende dalla sua area.

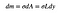
Infine, ho bisogno di ottenere L in termini di y. Lo farò anche io prima di ottenere un’espressione in termini di x. Posso chiamare il lato sinistro del rettangolo ” x “e il lato destro”s”. Questo significa che:

Ma il lato sinistro del triangolo che può essere descritto come una linea con l’equazione:

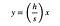
Dove (h/s) è la pendenza. Posso risolvere questa equazione per x e sostituire l’espressione per L.

Come un rapido controllo di realtà. Assicuriamoci che le cose funzionino prima di andare troppo lontano. E se lasciassimo y = h? Questo dovrebbe essere nella parte superiore del triangolo con una lunghezza rettangolare di zero. Si’. Funziona. Che dire di y = 0? Il rettangolo dovrebbe avere una lunghezza di s. Sembra buono.

Ora ho solo bisogno di mettere insieme tutte queste cose. Questa è la massa di quella fetta di un rettangolo.

La “s” annulla FTW (per la vittoria).

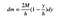
questo è abbastanza buono per ora. Il prossimo passo è scrivere un’espressione per il centro di massa y. Dato che lascerò che la larghezza di questo pezzo vada a zero, otterrò un integrale invece di una somma.

posso integrare questo, ma è più facile se rompo in due parti. Solo un po ‘ di algebra mi dà:

Ora posso integrare. Ecco cosa ottengo.

Valutare al limite (che è semplice, visto che il limite inferiore è pari a zero):

il Boom. Questo è il centro y di massa. Ha anche unità di distanza (che dovrebbe). Inoltre, si noti che il centro di massa y non dipende dalla lunghezza del triangolo nella direzione x (il parametro s). Che figata. Significa anche che possiamo facilmente trovare il centro x di massa. Tutto quello che devo fare è rompere lo stesso triangolo in rettangoli verticali.

Al fine di rendere la matematica stessa in direzione x, avrei bisogno di spostare l’origine in un altro angolo del triangolo. Ciò significa che il centro di massa x è (1/3) s dal lato destro. Questo dà un totale centro di massa di:

Cool.

Calcolo numerico del centro di massa

Oh, pensavi che fossi finito? Non ho finito. Che ne dici di questo-un calcolo numerico del centro di massa? Sì, sarà divertente. Ecco il mio piano.

• Scegli le dimensioni effettive di un triangolo. Non posso fare un calcolo numerico con le variabili. Mi servono i numeri. Userò s = 4, h = 1. Sì, ci dovrebbero essere unità, ma non importa. OK, la densità dell’area è 1 (dovrebbe essere chiaro che non importa).
• Scegli una piccola dimensione del passo. Diciamo che ho piccoli blocchi con dimensioni di 0,01 per 0,01. Trova la posizione vettoriale di questo blocco e la sua massa (tutti i blocchi hanno la stessa massa).
• Usa la versione formula somma del centro di massa.
• Sposta il blocco fino a coprire tutte le parti del triangolo.

Facciamo questo. OK, c’è una piccola difficoltà. Ho bisogno di fare un ciclo all’interno di un ciclo. Il ciclo interno sarà l’aggiunta di piazze lungo l’asse x dal versante sinistro di x = h. Il ciclo esterno, sarà lo spostamento delle righe orizzontali da 0 a h.

Qui è la parte principale del codice il codice completo qui):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

Con un pezzo risoluzione di 0.01, 0.01, ottengo il seguente:

Sì, sono abbastanza contento di questo.