Come ricordi il punto su un’isola deserta dove hai sepolto il tuo tesoro? Si sceglie un punto di riferimento, dire una palma, e misurare quanti passi nord/sud e quanti passi est/ovest si deve andare da quel punto di riferimento per arrivare al tesoro. È un’idea semplice ma, sorprendentemente, i matematici hanno impiegato secoli per sviluppare il suo pieno potenziale nel proprio campo. Quando finalmente lo hanno fatto, ha rivoluzionato la matematica riunendo due aree che a prima vista hanno poco a che fare l’una con l’altra: algebra e geometria.
Quando iniziamo ad imparare la geometria, di solito pensiamo a forme semplici come linee, triangoli e cerchi nel piano bidimensionale. È possibile costruire queste e forme più complicate utilizzando un righello, bussole e goniometro. Gli antichi greci erano maestri in questo tipo di geometria: usando solo bussole e una retta (un righello non marcato) erano in grado di costruire una gamma di forme e potevano persino dimostrare risultati matematici, come il teorema di Pitagora, usando questi semplici strumenti.
Ci sono alcune cose, tuttavia, che non puoi fare usando questi metodi di base. Due forme, ad esempio una linea e un cerchio, possono o non possono intersecarsi, e possono intersecarsi in modi diversi: forse la linea tocca solo il cerchio, forse si rade un piccolo arco fuori di esso, o forse lo taglia a metà. Per registrare queste informazioni è necessario un modo di descrivere le posizioni delle forme.
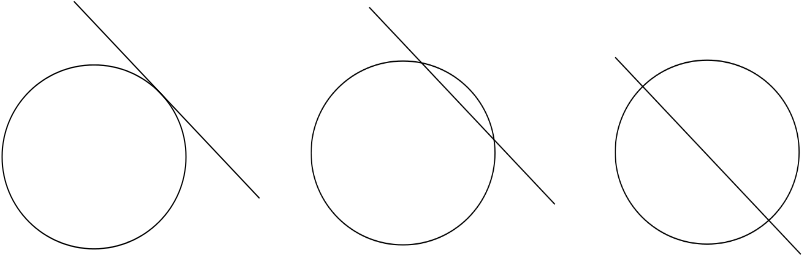
È qui che l’idea dell’isola del tesoro diventa utile. Illustra quello che viene chiamato il sistema di coordinate cartesiane. Scegli un punto nel piano, chiamato origine, e disegna due assi perpendicolari attraverso di esso, uno orizzontale e uno verticale. Qualsiasi punto del piano può essere raggiunto dall’origine percorrendo una certa distanza \(x\) lungo l’asse orizzontale e una certa distanza \(y\) lungo l’asse verticale. I numeri \((x, y)\) sono le coordinate del punto. L’origine stessa ha coordinate \ ((0,0)\). La parte dell’asse orizzontale (chiamata anche asse \(x\)) che si trova a sinistra dell’origine e la parte dell’asse verticale (l’asse \(y\)) sotto l’origine sono descritte da numeri negativi.
Le coordinate cartesiane prendono il nome dal filosofo e matematico francese René Descartes del xvii secolo. C’è una storia (probabilmente falsa) che Descartes ha inventato queste coordinate mentre giaceva a letto guardando una mosca sul soffitto e chiedendosi come descrivere la sua posizione. La propensione di Cartesio a giacere a letto fino a mezzogiorno potrebbe essere stata la causa della sua scomparsa, avvenuta a Stoccolma nel 1650. Cartesio era in Svezia per fare da tutor di matematica alla regina Cristina, che purtroppo preferiva lavorare la mattina presto. Secondo alcuni rapporti furono queste prime ore e le temperature scandinave a causare la polmonite che alla fine lo uccise. Altri hanno suggerito che fu avvelenato da un prete cattolico preoccupato per la teologia radicale di Cartesio.
In entrambi i casi, il sistema di coordinate cartesiane è uno dei lasciti più importanti di Cartesio (anche se non era l’unica persona ad avere l’idea). Ci permette di rispondere a problemi geometrici usando l’algebra e di visualizzare relazioni algebriche che altrimenti rimarrebbero piuttosto astratte. Prendiamo ad esempio l’equazione \ Possiamo tracciare il grafico di questa funzione in un sistema di coordinate cartesiane tracciando tutti i punti le cui coordinate sono della forma \((x, 2x-1)\): punti come \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), e \((1.73, 2.46)\). In questo caso il grafico è una linea retta che incontra l’asse \(y\) nel punto \(0,-1)\) e ha una pendenza di \(2\).
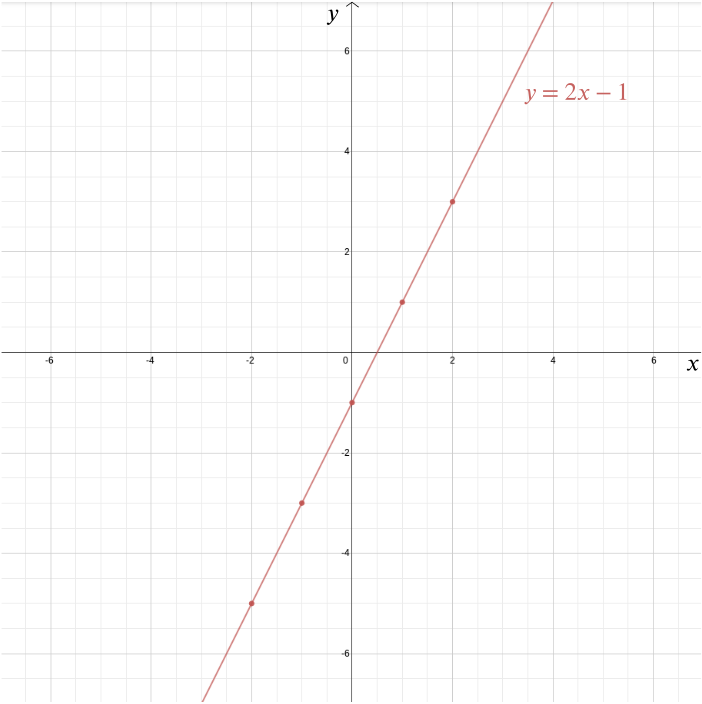
Più in generale, ogni retta è data da un’equazione della forma \ dove \(m\) indica la pendenza della retta e \((0,b)\) è il punto in cui attraversa il \(y\)-asse. Una linea verticale che non attraversa l’asse \(y\) è data da un’equazione della forma \(x=c\). In questo caso \((c,0)\) è il punto in cui attraversa l’asse \(x\).
Che dire di un cerchio? Un cerchio è costituito da tutti quei punti che si trovano alla stessa distanza \(r\) da un dato punto \(m\). Supponiamo che \(m\) sia il punto \((0,0)\). Dal teorema di Pitagora sappiamo che se un punto \((x, y)\) si trova alla distanza \(r\) da \((0,0)\), allora \
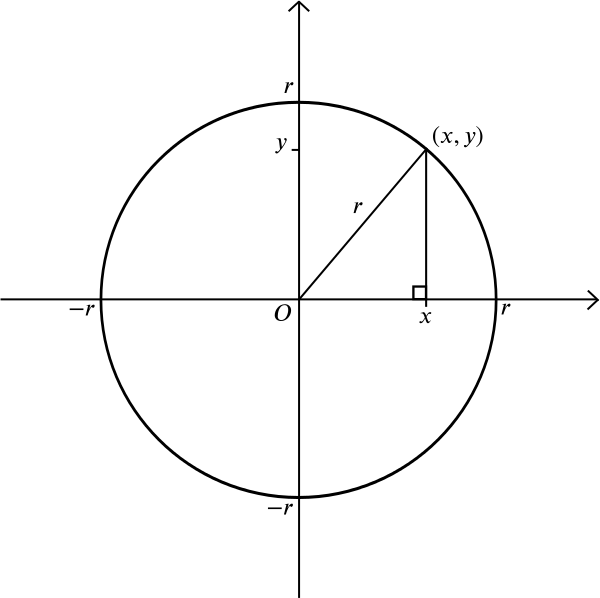
Questa è quindi l’equazione di un cerchio di raggio \(r\) centrato sull’origine. Puoi capire da solo che un cerchio di raggio \ (r\) centrato sul punto \((a, b)\) ha l’equazione \ Ma ecco una domanda più complicata: che forma si ottiene se si considerano tutti i punti che si trovano alla stessa distanza da un dato punto e una data linea? Senza un sistema di coordinate, si potrebbe disegnare il punto e la linea e sperimentare con il righello o bussole. Potresti disegnare alcuni punti che si trovano ad uguale distanza da entrambi e vedere se riesci a indovinare la forma generale.
Armato di un sistema di coordinate, tuttavia, la risposta diventa molto più semplice e molto più precisa. Supponiamo che il punto dato sia a distanza \(1\) dalla linea data. Poniamo il punto dato all’origine e la linea data in modo che sia orizzontale, dato dall’equazione \ Dal teorema di Pitagora la distanza di qualsiasi punto \((x,y)\) da \((0,0)\) è \(\sqrt{x^2 + y^2}\). La distanza da un punto \((x, y)\) alla linea \(y = -1\) è \(/y + 1/\) (usiamo il valore assoluto qui perché la coordinata\(y\) potrebbe essere negativa). Se questi due sono uguali, allora \ Quadrare entrambi i lati dà \ Riarrangiamento dà \ Quindi qualsiasi punto alla stessa distanza dal punto \((0,0)\) e la linea \(y=-1\) ha coordinate \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Puoi verificare tu stesso che anche il contrario è vero: ogni punto con queste coordinate si trova alla stessa distanza dal punto \((0,0)\) e dalla linea \(y=-1\).
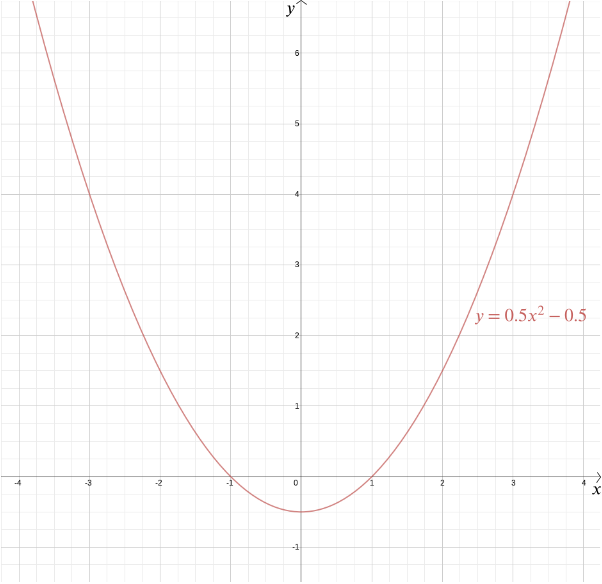
Siamo in grado di tracciare il grafico di questa funzione per vedere la forma, che si rivela essere una parabola. Infatti, ogni funzione quadratica \ per \(a\), \(b\) e \(c\) costanti, ci dà una parabola. Questa forma familiare, che può venire in tante variazioni sottili-lunga e sottile o tozza e piatta – è catturata da questa pratica espressione algebrica. Il fatto che oggi i termini “funzione quadratica” e “parabola” siano quasi considerati sinonimi evidenzia quanto sia stata efficace l’idea di Cartesio. Più in generale, qualsiasi relazione algebrica tra due variabili \(x\) e \(y\) ci dà una curva che possiamo tracciare usando le coordinate cartesiane.
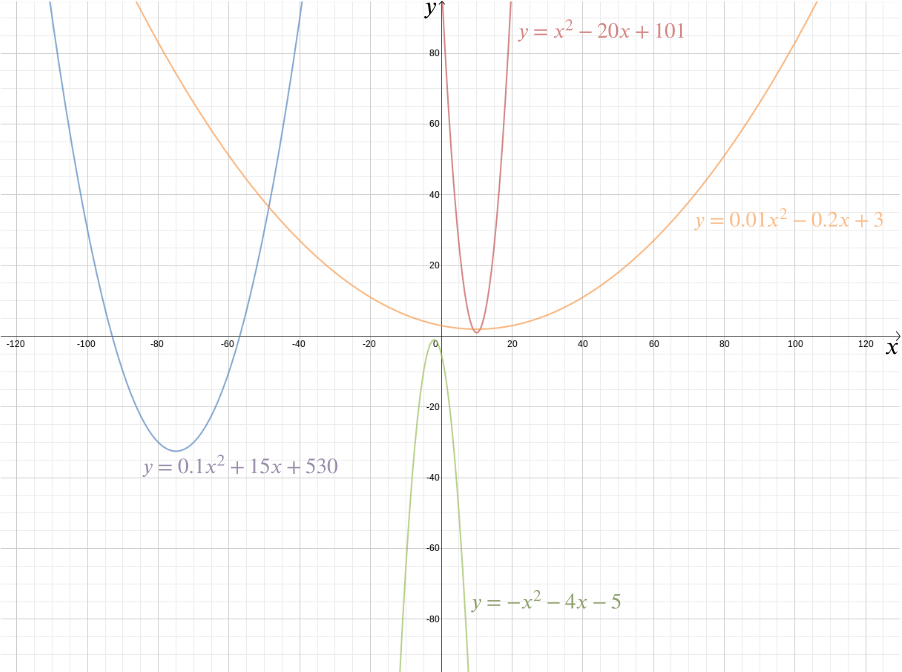
La rappresentazione algebrica rende facile rispondere a tutta una serie di domande geometriche. Per scoprire i punti di intersezione della linea data da \ e la parabola \(y = \frac{x^2}{2} – \frac{1}{2}\), abbiamo semplicemente notare che il \(y\) coordinate di un qualsiasi punto \((x,y)\) di entrambe devono soddisfare entrambe le equazioni, quindi, \ Questo dà \ Risolvendo l’equazione otteniamo \ e \ quindi i punti di intersezione sono a \
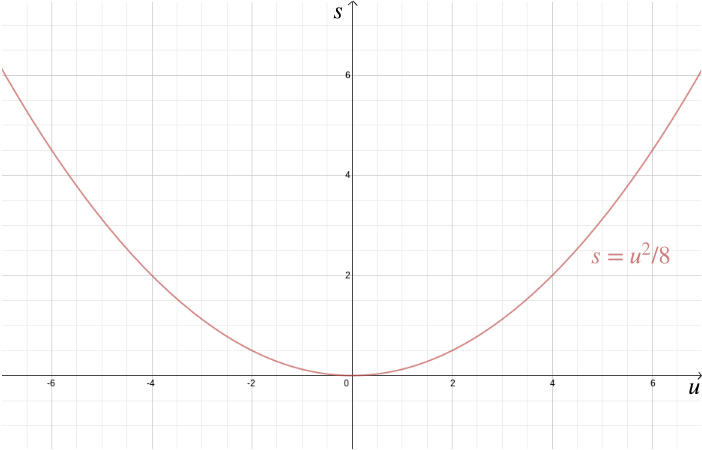
Oltre a risolvere i problemi di geometria, coordinate Cartesiane anche aiutarti a visualizzare algebrica relazioni. Ad esempio, supponiamo che un’auto stia viaggiando a velocità \(u\) e che il conducente stia azionando i freni, determinando una decelerazione costante, ad esempio, di \(-4\) metri/secondi\(^2\). La distanza di arresto \(s\) – la distanza che l’auto copre prima che si fermi – è data dalla relazione algebrica \ Tracciando questo usando le coordinate cartesiane porta a casa quanto sia importante rallentare nelle aree urbane, perché la distanza di arresto aumenta rapidamente con \(u\).
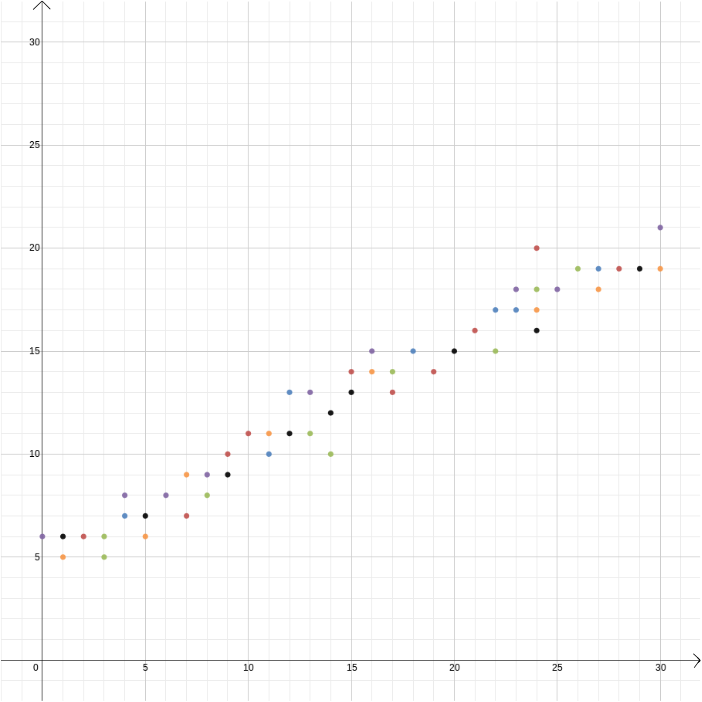
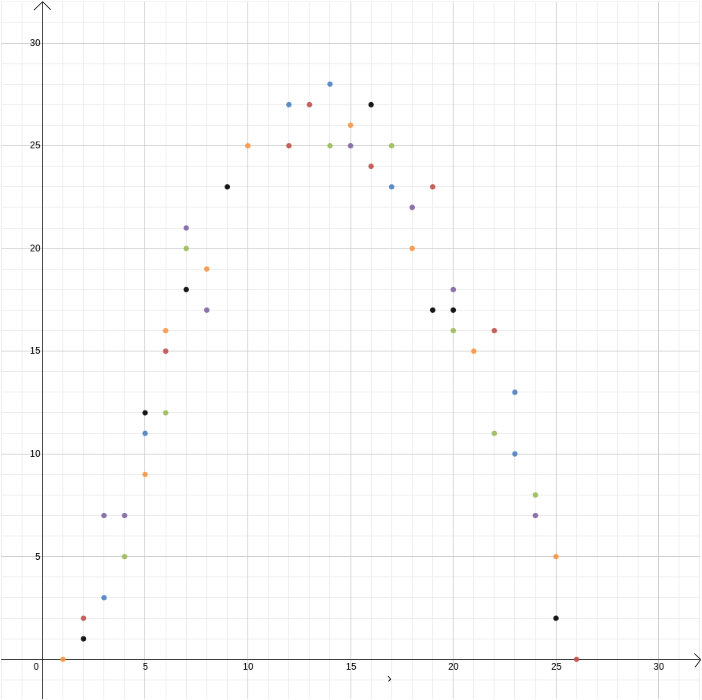
In questo esempio abbiamo saputo che la relazione tra due variabili, in quanto può essere derivata dalle leggi della fisica. Ma le coordinate cartesiane sono utili anche quando sospetti che due variabili siano correlate ma non sai come. Supponiamo che pensiamo che ci sia una relazione tra il profitto realizzato da un venditore di gelati e la temperatura esterna. Per scoprire quale potrebbe essere quella relazione, possiamo misurare la temperatura e il profitto, ad esempio, nel corso di un anno e tracciare i valori l’uno contro l’altro, con la temperatura registrata sull’asse \(x\) e il profitto sull’asse \(y\). Possiamo quindi vedere se possiamo individuare uno schema. Nel primo diagramma qui sotto potremmo indovinare che la relazione è lineare, e possiamo provare a trovare la linea retta \ che meglio si adatta ai nostri dati (ci sono metodi per trovare questa soluzione migliore). Nel secondo diagramma sottostante potremmo indovinare che la relazione è quadratica e di nuovo possiamo provare a trovare la funzione \ che meglio si adatta ai dati.
Le coordinate cartesiane hanno svolto un ruolo importante nello sviluppo del calcolo nella seconda metà del xvii secolo. Il calcolo consente di elaborare attributi di curve come la loro pendenza in un dato punto o l’area della regione che si trova tra una curva e l’asse \(x\). Questi possono avere anche interpretazioni fisiche. Per esempio, se riportiamo la distanza di viaggio contro il tempo che è stato in viaggio, la pendenza della curva risultante in un dato momento—il tasso di variazione della distanza rispetto al tempo—rappresenta la velocità alla quale l’auto stava viaggiando in quel momento nel tempo: è la derivata della funzione, che ci dà la distanza in termini di tempo. Vedi anche Perché i gradienti sono importanti nel mondo reale?.
Possiamo anche salire di una dimensione considerando un terzo asse perpendicolare ai primi due, che puoi immaginare come uscire dal tuo foglio di carta e puntare verso di te. Usando un tale sistema tridimensionale ora puoi rappresentare oggetti tridimensionali e visualizzare come una terza variabile \(z\) dipende dai tuoi primi due, \(x\) e \(y\).
Questi esempi dovrebbero darti un senso del perché le coordinate sono diventate così indispensabili in tutte le aree della scienza, dalla fisica all’astronomia e all’ingegneria, e anche nelle industrie visive per produrre computer grafica e le immagini generate dal computer che ammiriamo nei film e nei giochi.
Nella matematica stessa il legame tra algebra e geometria è culminato in un’intera area chiamata geometria algebrica, che detiene un fascino proprio. Forse il risultato più famoso che è emerso da quest’area è l’ultimo Teorema di Fermat, dal nome di un contemporaneo di Cartesio, Pierre de Fermat, che ha anche contribuito in modo significativo allo sviluppo del sistema di coordinate cartesiane. Fermat stava considerando una domanda che collega la geometria alla teoria dei numeri. Secondo il teorema di Pitagora, se \(a\), \(b\) e \(c\) sono i lati di un triangolo rettangolo e \(c\) è il lato opposto all’angolo retto, quindi \(a^2 + b^2 = c^2\). Ci sono infinitamente molte triple di numeri interi \(a\), \(b\) e \(c\) che soddisfano questa relazione; \((3,4,5)\) è un esempio.
Ora supponiamo di cambiare l’esponente e considerare espressioni come \ e \ e più in generale \ dove \(n\) è un numero naturale maggiore di \(2\). Possiamo ancora trovare numeri interi positivi \(a\), \(b\) e \(c\) che soddisfano l’equazione? Fermat sospettava che non possiamo e ha scarabocchiato tanto nel margine del suo libro di testo di matematica, dicendo che aveva una “prova meravigliosa” per quel fatto che il margine era troppo stretto per contenere.
Quello scarabocchio doveva perseguitare i matematici per oltre 350 anni. Non è stato fino al 1994 che una prova corretta di questo risultato apparentemente innocuo è stato finalmente annunciato dal matematico Andrew Wiles. Wiles aveva fatto ampio uso di geometria algebrica. In particolare, aveva usato i risultati riguardanti le curve ellittiche descritte da punti nel piano le cui coordinate soddisfano la contemplazione di una mosca di Cartesio ha fatto molta strada!
