C’è più di un modo per sommare una serie infinita. Cesàro summation consente di calcolare la somma di serie che non hanno una somma in senso classico.
Supponiamo di avere una serie infinita
L’ennesima somma parziale della serie è data da
La classica somma della serie, se esiste, è definita come il limite delle sue somme parziali. Cioè,
Cesàro summation adotta un approccio diverso. Invece di prendere il limite delle somme parziali, prende il limite delle medie delle somme parziali. Per essere precisi, definire
e definire la somma di Cesàro come limite del Cn quando n va all’infinito. Se una serie ha una somma nel senso classico, ha anche una somma nel senso Cesàro, e i limiti sono gli stessi. Ma alcune serie hanno una somma Cesàro che non hanno una somma classica. O forse esistono entrambi i limiti ma i passaggi intermedi della somma di Cesàro si comportano meglio, come vedremo in un esempio qui sotto.
Se si esprime il Cn in termini di originale e termini si ottiene
In altre parole, l’ennesimo Cesàro somma parziale è una riponderazione dei classici somme parziali, con i pesi cambiare in funzione di n. Nota che per il fisso che ho, la frazione di moltiplicazione ai va a 1 quando n aumenta.
Somma di Fejér e fenomeno di Gibbs
La somma di Fejér è la somma di Cesàro applicata alla serie di Fourier. Le somme parziali (ordinarie) di una serie di Fourier danno la migliore approssimazione a una funzione misurata dalla norma dei minimi quadrati. Ma le somme parziali di Cesàro possono essere qualitativamente più simili alla funzione approssimata. Dimostriamo questo sotto con un’onda quadra.
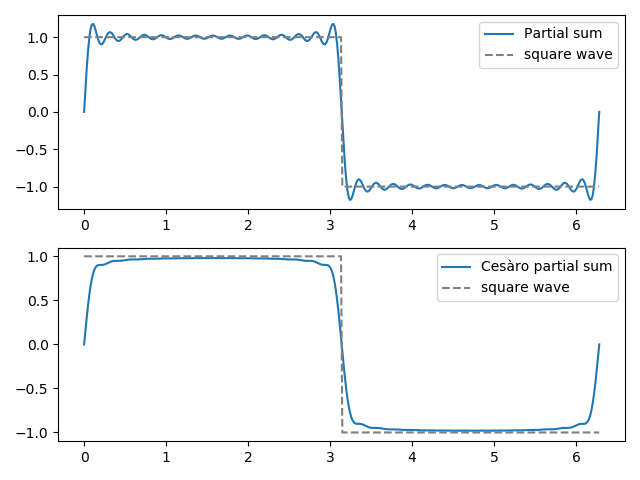
La somma parziale ordinaria 30 mostra gli inizi del fenomeno Gibbs, le “orecchie di pipistrello” nella parte superiore dell’onda quadra e la loro immagine speculare in basso. La somma parziale del 30 ° Cesàro è più liscia ed elimina i fenomeni di Gibbs in prossimità della discontinuità nell’onda quadra.
Altri messaggi della serie di Fourier
- Serie di Fourier-Bessel
- Controesempio al principio di Dirichlet
- Onde sinusoidali ritagliate
