hogyan emlékszel arra a helyre egy lakatlan szigeten, ahol eltemetted a kincsedet? Kiválasztasz egy mérföldkövet, mondjuk egy pálmafát, és megméred, hány lépést kell megtenned északra/délre, és hány lépést kell megtenned keletre/nyugatra attól a mérföldkőtől, hogy eljuss a kincshez. Ez egy egyszerű ötlet, de meglepő módon a matematikusoknak évszázadokra volt szükségük ahhoz, hogy teljes potenciáljukat saját területükön fejlesszék. Amikor végül megtették, forradalmasította a matematikát azáltal, hogy két olyan területet hozott össze, amelyeknek kevés köze van egymáshoz: algebra és geometria.
amikor elkezdjük tanulni a geometriát, általában olyan egyszerű alakzatokra gondolunk, mint a vonalak, háromszögek és körök a kétdimenziós síkban. Ezeket a bonyolultabb alakzatokat vonalzó, iránytű és szögmérő segítségével készítheti el. Az ókori görögök mesterek voltak az ilyen típusú geometriában: segítségével csak iránytű és egy egyenes él (egy jelöletlen vonalzó) képesek voltak építeni egy sor formák és tudták bizonyítani matematikai eredmények, mint például a Pitagorasz-tétel, ezekkel az egyszerű eszközökkel.
vannak azonban bizonyos dolgok, amelyeket nem lehet megtenni ezekkel az alapvető módszerekkel. Két alakzat, mondjuk egy vonal és egy kör, keresztezheti vagy nem keresztezheti egymást, és különböző módon metszhetik egymást: lehet, hogy a vonal csak megérinti a kört, talán leborotvál egy kis ívet róla, vagy talán kettévágja. Ezen információk rögzítéséhez szükség van az alakzatok helyének leírására.
itt hasznos a kincses sziget ötlete. Ez szemlélteti az úgynevezett Derékszögű koordináta-rendszert. Válasszon egy pontot a síkban, az úgynevezett Origót, és rajzoljon rajta két merőleges tengelyt, egy vízszintes és egy függőleges. A sík bármely pontját el lehet érni a kiindulási ponttól úgy, hogy a vízszintes tengely mentén egy bizonyos távolságot \(x\), a függőleges tengely mentén pedig egy bizonyos távolságot \(y\) megteszünk. A \((x,y)\) számok a pont koordinátái. Maga az eredet koordinátákkal rendelkezik \((0,0)\). A vízszintes tengelynek (más néven \(x\)-tengelynek) az Origótól balra fekvő részét, valamint a függőleges tengelynek (\(y\)-tengelynek) az Origó alatti részét negatív számok írják le.
a derékszögű koordinátákat a 17.századi francia filozófusról és matematikusról, Descartes-ról nevezték el. Van egy (valószínűleg nem igaz) történet, hogy Descartes találta ki ezeket a koordinátákat, miközben az ágyban feküdt, és a mennyezeten lévő legyet nézte, és azon tűnődött, hogyan írja le a helyét. Descartes hajlandósága arra, hogy délig feküdjön az ágyban, valójában oka lehetett halálának, amely 1650-ben történt Stockholmban. Descartes Svédországban volt, hogy Christina királynő matematikai oktatójaként járjon el, aki sajnos inkább kora reggel dolgozott. Egyes jelentések szerint a korai órák és a skandináv hőmérséklet okozta a tüdőgyulladást, amely végül megölte. Mások szerint egy katolikus pap mérgezte meg, aki Descartes radikális teológiája miatt aggódott.
Akárhogy is, a derékszögű koordinátarendszer Descartes egyik legfontosabb öröksége (bár nem ő volt az egyetlen, akinek ötlete volt). Lehetővé teszi számunkra, hogy az algebra segítségével válaszoljunk a geometriai problémákra, és olyan algebrai kapcsolatokat jelenítsünk meg, amelyek egyébként meglehetősen elvontak maradnának. Vegyük például az egyenletet \ ennek a függvénynek a grafikonját egy derékszögű koordinátarendszerben ábrázolhatjuk úgy,hogy minden olyan pontot ábrázolunk, amelynek koordinátái \((x, 2x-1)\): olyan pontok, mint \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), és \((1.73, 2.46)\). Ebben az esetben a gráf egy egyenes,amely a \((0, -1)\) pontban megfelel a \(y\)-tengelynek, meredeksége pedig \(2\).
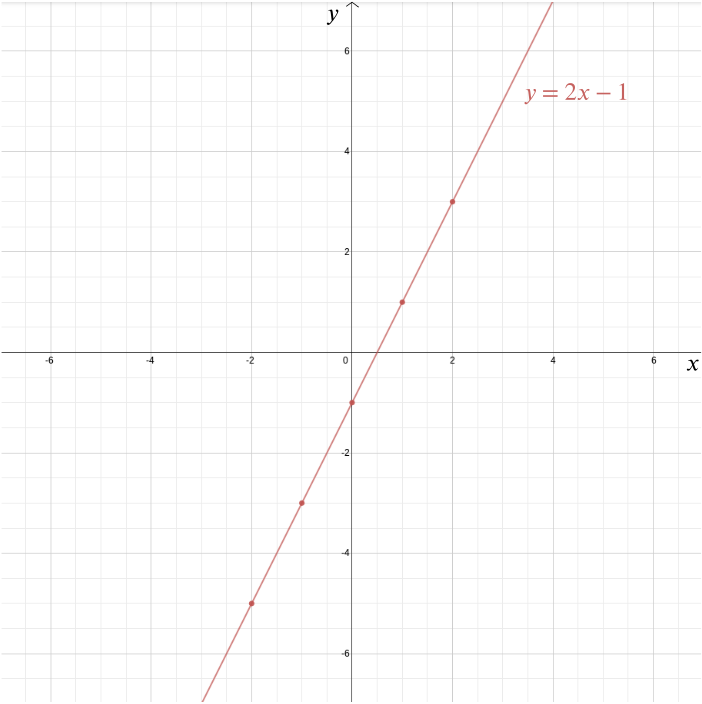
általánosabban minden egyenest egy \ alakú egyenlet ad meg,ahol \(m\) megadja az egyenes meredekségét és \((0, b)\) az a pont, ahol keresztezi az \(y\) tengelyt. A \(y\) tengelyt nem keresztező függőleges vonalat a \(x=c\) alakú egyenlet adja meg. Ebben az esetben \((c, 0)\) az a pont, ahol keresztezi a \(x\) tengelyt.
mi a helyzet egy körrel? A kör mindazokból a pontokból áll, amelyek egyenlő távolságban fekszenek \(r\) egy adott ponttól \(m\). Tegyük fel, hogy \(m\) a \((0,0)\) pont. Pythagoras tételéből tudjuk, hogy ha egy \((x, y)\) pont \(r\) távolságra fekszik \((0,0)\) – től, akkor \
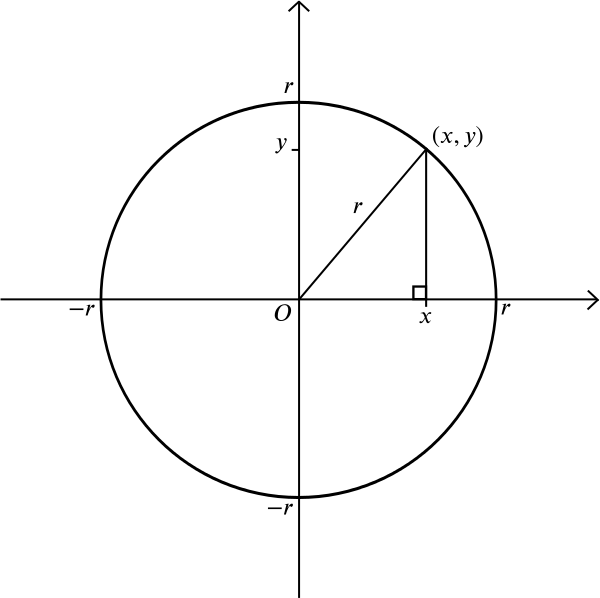
Ez tehát egy \(r\) sugarú kör egyenlete, amelynek középpontja az Origó. Akkor dolgozzanak ki magad, hogy egy kör sugara \(r\) középpontja a pont \((a, b)\) van az egyenlet \ de itt van egy bonyolultabb kérdés: milyen alakot kapunk, ha figyelembe vesszük az összes pontot, amelyek egyenlő távolságra vannak egy adott ponttól és egy adott vonaltól? Koordináta-rendszer nélkül megrajzolhatja a pontot és a vonalat, és kísérletezhet a vonalzóval vagy az iránytűvel. Rajzolhat néhány pontot, amelyek egyenlő távolságra fekszenek mindkettőtől, és megnézheti, hogy kitalálhatja-e az Általános alakot.
koordinátarendszerrel felfegyverkezve azonban a válasz sokkal könnyebbé és sokkal pontosabbá válik. Tegyük fel, hogy az adott pont \(1\) távolságra van az adott vonaltól. Tegyük az adott pontot az Origóra és az adott vonalat úgy, hogy vízszintes legyen, a Pythagoras-tétel \ egyenletével megadva bármely pont \((x,y)\) távolsága \((0,0)\)\) \(\sqrt{x^2 + y^2}\). A \((x,y)\) ponttól a \(y = -1\) vonalig terjedő távolság \(|y+1|\) (Itt az abszolút értéket használjuk, mert a \(y\)-koordináta negatív lehet). Ha ez a kettő egyenlő, akkor a \ Négyszögesítés mindkét oldalon \ átrendezést ad \ tehát bármely pont egyenlő távolságra van a \((0,0)\) ponttól és az \(y=-1\) vonalnak koordinátái vannak \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Saját maga is ellenőrizheti, hogy az ellenkezője is igaz – e: minden pont ezekkel a koordinátákkal egyenlő távolságra van a \((0,0)\) ponttól és a \(y=-1\) vonaltól.
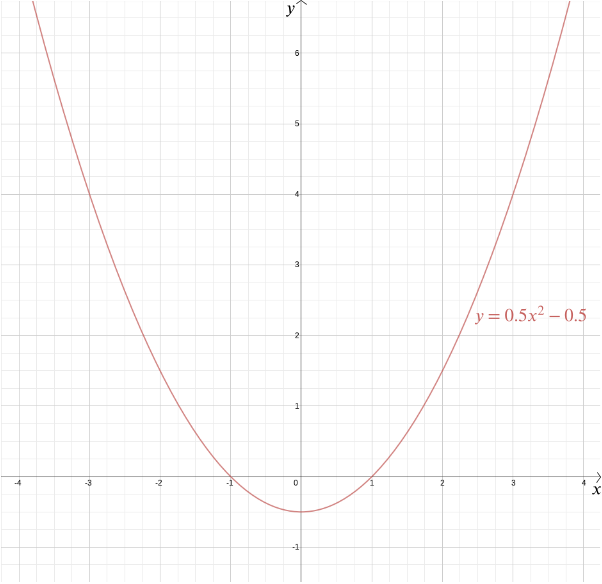
ennek a függvénynek a grafikonját ábrázolhatjuk a kívánt alak megtekintéséhez, amely kiderül, hogy parabola. Valójában minden \ kvadratikus függvény \(A\), \(b\) és \(c\) konstansokra parabolát ad. Ezt az ismerős formát, amely oly sok finom változatban jöhet létre—hosszú és vékony vagy guggolt és lapos—megragadja ez a praktikus algebrai kifejezés. Az a tény, hogy ma a “másodfokú funkció” és a “parabola” kifejezéseket szinte szinonimának tekintik, rávilágít arra, hogy Descartes ötlete mennyire sikeres volt. Általánosabban, bármely algebrai kapcsolat két változó között \(x\) és \(y\) ad nekünk egy görbét, amelyet derékszögű koordinátákkal ábrázolhatunk.
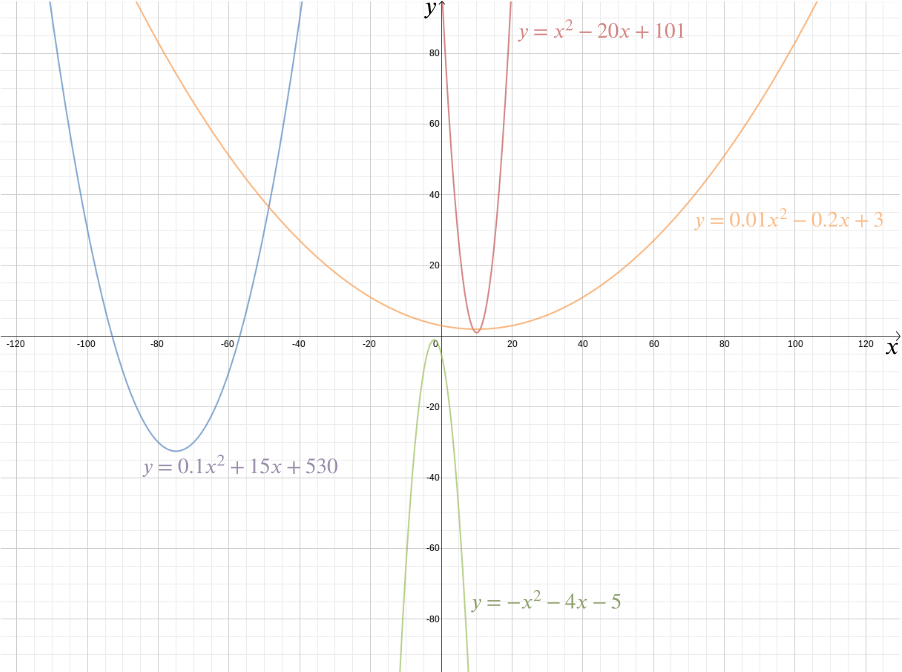
az algebrai ábrázolás megkönnyíti a geometriai kérdések egész sorának megválaszolását. A \ és a parabola \(y = \frac{x^2}{2} – \frac{1}{2}\) által megadott vonal metszéspontjainak kidolgozásához egyszerűen megjegyezzük, hogy bármely \((x,y)\) mindkét ponton fekvő \((y\) koordinátának meg kell felelnie mindkét egyenletnek, így \ ez megadja \ a kapott kvadratikus egyenlet megoldását \ és \ tehát a metszéspontok \
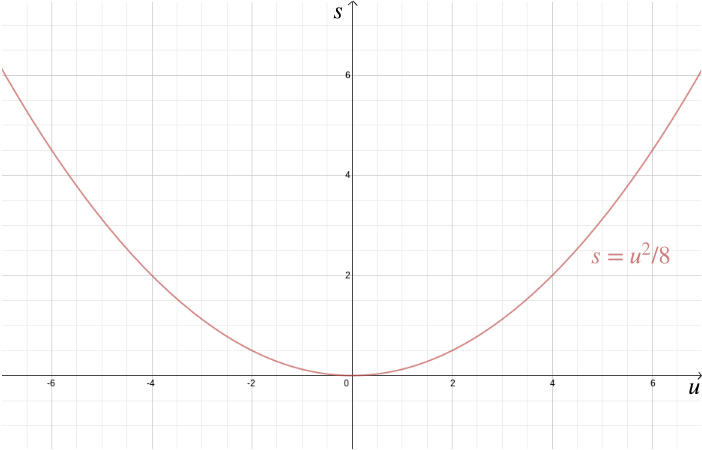
a geometriai problémák megoldásán kívül a derékszögű koordináták segítenek az algebrai kapcsolatok megjelenítésében is. Tegyük fel például, hogy egy autó \(u\) sebességgel halad, és a vezető fékez, ami állandó lassulást eredményez, például \(-4\) méter/másodperc\(^2\). A megállási távolság \(s\)—az a távolság, amelyet az autó megtart, mielőtt megállna—az algebrai kapcsolat adja \ ennek ábrázolása derékszögű koordinátákkal hozza haza, hogy mennyire fontos a városi területeken lelassulni, mert a féktávolság gyorsan növekszik \(u\).
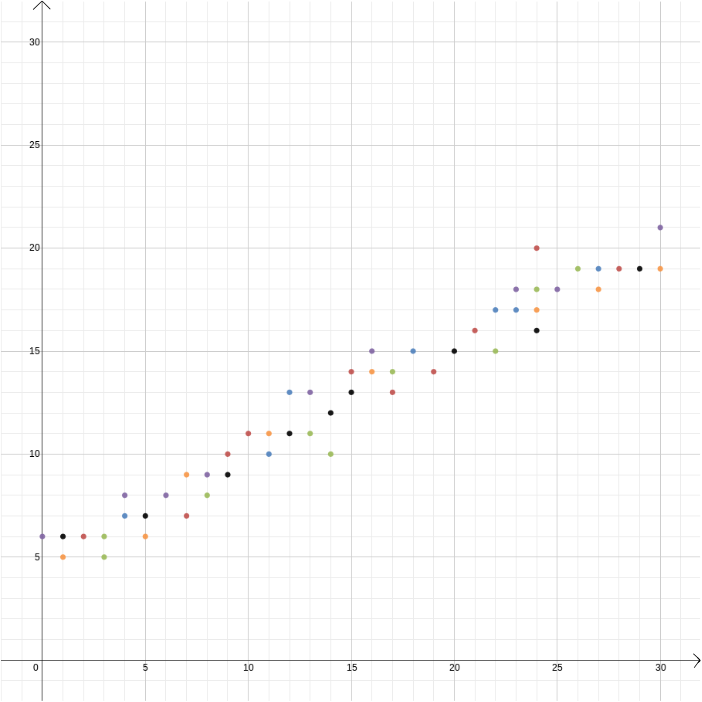
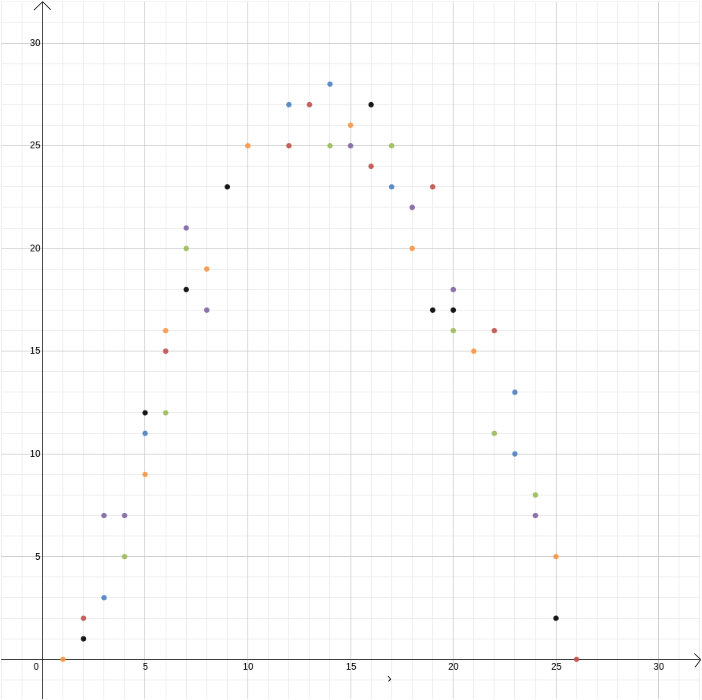
ebben a példában két változó kapcsolatát ismertük, mert a fizika törvényeiből származtatható. De a derékszögű koordináták akkor is hasznosak, ha gyanítja, hogy két változó összefügg, de nem tudja, hogyan. Tegyük fel, hogy úgy gondoljuk, hogy kapcsolat van a fagylalt eladó által elért nyereség és a külső hőmérséklet között. Hogy megtudjuk, mi lehet ez a kapcsolat, megmérhetjük a hőmérsékletet és a profitot, mondjuk egy év folyamán, és ábrázolhatjuk az értékeket egymás ellen, a hőmérsékletet az \(x\) tengelyen, a profitot pedig az \(y\) tengelyen. Ezután láthatjuk, hogy észlelhetünk-e egy mintát. Az alábbi első ábrán azt sejthetjük, hogy a kapcsolat lineáris, és megpróbálhatjuk megtalálni az adatainknak legjobban megfelelő \ egyeneset (vannak módszerek ennek a legmegfelelőbb megtalálására). Az alábbi második ábrán azt sejthetjük, hogy a kapcsolat másodfokú, és ismét megpróbálhatjuk megtalálni azt a \ függvényt, amely a legjobban megfelel az adatoknak.
a derékszögű koordináták nagy szerepet játszottak a számítás fejlesztésében a 17.század második felében. Kalkulus lehetővé teszi, hogy dolgozzanak ki attribútumokat görbék, mint a meredekség egy adott ponton, vagy a terület a régió között fekszik egy görbe és a \(x\)-tengely. Ennek fizikai értelmezése is lehet. Például, ha azt a távolságot ábrázoljuk, amelyet egy autó megtett a megtett idővel szemben, akkor a kapott görbe meredeksége egy adott időben—a távolság időbeli változásának sebessége—azt a sebességet jelenti, amellyel az autó az adott pillanatban haladt: ez a függvény deriváltja, amely megadja nekünk a távolságot az idő szempontjából. Lásd még: Miért fontosak a színátmenetek a Való Világban?.
egy dimenzióval is feljebb léphetünk, ha figyelembe vesszük az első kettőre merőleges harmadik tengelyt, amelyet úgy képzelhetünk el, mintha kijönne a papírlapodból, és rád mutatna. Egy ilyen háromdimenziós rendszer segítségével háromdimenziós objektumokat ábrázolhatunk, és megjeleníthetjük, hogy a harmadik változó \(z\) hogyan függ az első kettőtől, \(x\) és \(y\).
ezeknek a példáknak némi megértést kell adniuk arról, hogy a koordináták miért váltak annyira nélkülözhetetlenné a tudomány minden területén, a fizikától a csillagászatig és a mérnöki tudományig, valamint a vizuális iparágakban a számítógépes grafika és a számítógéppel generált képek előállításához, amelyeket a filmekben és játékokban csodálunk.
magában a matematikában az algebra és a geometria közötti kapcsolat az algebrai geometriának nevezett egész területen tetőzött, amely saját magával ragadó. Talán a leghíresebb eredmény, amely ezen a területen jelent meg, Fermat utolsó tétele, amelyet Descartes kortársáról, Pierre de Fermatról neveztek el, aki szintén jelentősen hozzájárult a derékszögű koordinátarendszer fejlődéséhez. Fermat egy olyan kérdést fontolgatott, amely összekapcsolja a geometriát a számelmélettel. Pitagorasz tétele szerint, ha \(a\), \(b\) és \(c\) egy derékszögű háromszög oldala, és \(c\) a derékszöggel ellentétes oldal, akkor \(a^2 + b^2 = c^2\). Az \(a\), \(b\) és \(c\) egész számoknak végtelen sok hármasa van, amelyek kielégítik ezt a kapcsolatot; \((3,4,5)\) egy példa.
tegyük fel, hogy megváltoztatjuk a kitevőt, és olyan kifejezéseket veszünk figyelembe, mint \ és \ és általánosabban \ ahol \(n\) egy \(2\) – nél nagyobb természetes szám. Találhatunk-e még pozitív egész számokat \(a\), \(b\) és \(c\), amelyek kielégítik az egyenletet? Fermat gyanította, hogy nem tudunk, és annyit firkált a matematikai tankönyvének margójába, mondván, hogy “csodálatos bizonyítéka” van erre a tényre, amelyet a margó túl szűk volt ahhoz, hogy tartalmazza.
Ez a firka több mint 350 évig kísértette a matematikusokat. Csak 1994-ben jelentette be Andrew Wiles matematikus ennek a látszólag ártalmatlan eredménynek a helyes bizonyítékát. Wiles tette széles körben használják algebrai geometria. Különösen, ő használta vonatkozó eredmények elliptikus görbék által leírt pontok a síkban, amelynek koordinátái megfelelnek \ Descartes ‘ szemlélődés egy légy hosszú utat!
