csináljuk ezt. Levezetem a tömegközéppont kifejezését egy derékszögű háromszögre. Miért?

látod, jól fogunk szórakozni. Már belefoglaltam egy Yoda mémet. Mi baj lehet?
itt van a háromszög.

ó, úgy néz ki, mint egy normál kék háromszög. Igaz? De tegyük fel, hogy ez egy vékony fémlemez, amelynek tömege M. hogyan találná meg a tömegközéppont helyét? Kezdjük a tömegközéppont alapvető meghatározásával.

Ez lényegében súlyozott átlag. Ez egy súlyozott átlag. De ha az objektumot egy csomó apró darabra bontjuk, akkor szorozzuk meg az egyes tömegek vektorpozícióját és annak apró tömegét. Ezután összeadjuk az összeset, és elosztjuk a teljes tömeggel. Ez a tömegközéppont. Itt egy másik kép.

természetesen ebben az esetben nincs egy csomó darabunk. Folyamatos tömegünk van. Ez azt jelenti, hogy ehelyett az összeget integrálvá alakíthatjuk. Ahelyett, hogy egyszerre foglalkoznék mind az x, mind az y irányokkal, csak az y tömegközéppontot fogom figyelembe venni.
azzal kezdem, hogy ezt a háromszöget egy csomó vízszintes téglalapra bontom. Itt van az egyik ilyen téglalap.

tehát ezeket a vékony téglalapokat felhasználhatom a tömegközéppont megtalálásához. Csak meg kell szorozni az egyes téglalapok helyzetét és az egyes téglalapok tömegét. A helyzet elég egyértelmű, “y”. A tömeg egy kicsit trükkösebb. Vegye figyelembe azt is, hogy a háromszög felfelé mozgó téglalapok esetében kisebbek, kisebb tömeggel.
ennek az apró téglalapnak a területének arányosnak kell lennie a területével. Hadd határozzam meg a terület sűrűségét az egész háromszög számára:

Ez azt jelenti, hogy az apró téglalap tömege a területétől függő apró érték (DM) lesz.
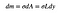
végül meg kell kapnom l szempontjából y. ezt úgy fogom megtenni, hogy először kifejezést kapok x. Hívhatom a téglalap bal oldalát ” x “- nek, a jobb oldalt pedig”s” – nek. Ez azt jelenti, hogy:

de a háromszög bal oldala a következő egyenlettel jellemezhető:
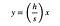
ahol (h / S) a meredekség. Megoldhatom ezt az egyenletet x-re, és helyettesíthetem az L kifejezéssel.

mit szólnál egy gyors valóság ellenőrzéshez. Csak győződjünk meg róla, hogy működnek a dolgok, mielőtt túl messzire megyünk. Mi van, ha hagyjuk, hogy y = h? Ennek a háromszög tetején kell lennie, amelynek téglalap hossza nulla. Ja. Ez működik. Mi a helyzet y = 0? A téglalapnak s hosszúságúnak kell lennie.
most már csak össze kell raknom ezeket a dolgokat. Ez a téglalap szeletének tömege.

az “S” törli az FTW-t (a győzelemért).
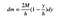
Ez most elég jó. A következő lépés egy kifejezés írása az y-tömegközéppontra. Mivel hagyom, hogy ennek a darabnak a szélessége nulla legyen, összeg helyett integráltat fogok kapni.

ezt integrálhatom, de könnyebb, ha két részre bontom. Csak egy kis algebra ad nekem:

most már integrálhatom. Itt van, amit kapok.

a határértékek értékelése (ami könnyű, mivel az alsó határ nulla):

boom. Ez a tömeg y-középpontja. Még távolságegységei is vannak (aminek meg kell lennie). Vegye figyelembe azt is, hogy az y-tömegközéppont nem függ a háromszög hosszától az x irányban (az s paraméter). Ez király. Ez azt is jelenti, hogy könnyen megtalálhatjuk az x-tömegközéppontot. Csak annyit kell tennem, hogy ugyanazt a háromszöget függőleges téglalapokra bontom.

annak érdekében, hogy a matematika azonos legyen az X irányban, át kell helyeznem az eredetet a háromszög másik sarkába. Ez azt jelenti, hogy az x – tömegközéppont (1/3) s a jobb oldalon. Ez a teljes tömegközéppont:

hűvös.
a tömegközéppont numerikus kiszámítása
Ó, azt hitted, hogy befejeztem? Még nem végeztem. Mit szólnál ehhez — a tömegközéppont numerikus kiszámítása? Igen, jó móka lesz. Itt van a tervem.
- válassza ki a háromszög tényleges méreteit. Nem tudok numerikus számítást végezni változókkal. Számok kellenek. S = 4, h=1-et fogok használni. Igen, kell lennie egységeknek, de ez nem számít. OK, a terület sűrűsége 1 (egyértelműnek kell lennie, hogy ez sem számít).
- válasszon egy apró lépésméretet. Tegyük fel, hogy apró blokkjaim vannak, amelyek mérete 0,01 x 0,01. Keresse meg a blokk vektor helyét és tömegét (minden blokk tömege azonos).
- használja a tömegközéppont összegképletének változatát.
- mozgassa a blokkot addig, amíg a háromszög minden része le nem fedődik.
csináljuk ezt. Oké, van egy kis nehézség. Meg kell csinálnom egy hurkot egy hurokban. A belső hurok négyzeteket ad össze az x tengely mentén a bal lejtőtől x = h-ig. a külső hurok ezeket a vízszintes sorokat 0-ról h-ra mozgatja.
itt van a kód fő része (teljes kód itt):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
0,01-0,01 darabmérettel a következőket kapom:

igen, én nagyon elégedett vagyok vele.
