Let ’ s tehdä tämän. Johdan lausekkeen massakeskipisteelle suorakulmaiselle kolmiolle. Miksi?

katso, meillä on hauskaa. Olen jo sisällyttänyt Yoda-meemin. Mikä voisi mennä vikaan?

tässä on kolmio.

oh, näyttää normaalilta siniseltä kolmiolta. Eikö niin? Mutta oletetaan, että kyseessä on jokin ohut metallilevy, jonka massa on M. miten löytäisit massakeskipisteen sijainnin? Aloitetaan massakeskipisteen perusmääritelmästä.

tämä on käytännössä painotettu keskiarvo. Se on painotettu keskiarvo. Mutta jos hajotat kappaleen pieniksi palasiksi, kerro jokaisen massan vektoriasento ja sen pieni massa. Sitten lisätään sitten kaikki ylös ja jaetaan kokonaismassalla. Se on massan keskipiste. Tässä on toinen kuva.

tietenkään tässä tapauksessa meillä ei ole kasaa palasia. Meillä on jatkuva massa. Se tarkoittaa, että voimme sen sijaan muuttaa summan integraaliksi. Sen sijaan, että käsittelisin sekä X-että y-suuntiin yhtä aikaa, aion vain harkita y-massakeskusta.

aloitan rikkomalla tämän kolmion joukoksi vaakasuoria suorakulmioita. Tässä on yksi niistä suorakulmioista.

niin, voin käyttää näitä laihoja suorakulmioita löytääkseni massakeskipisteen. Minun tarvitsee vain kertoa jokaisen suorakulmion sijainti ja massa. Asento on aika suoraviivainen, se on ”y”. Massa on hieman kinkkisempi. Huomaa myös, että suorakulmioita, jotka liikkuvat jopa kolmion, ne ovat pienempiä pienempi massa.

tämän pienen suorakulmion pinta-alan tulee olla verrannollinen sen pinta-alaan. Määrittelen koko kolmion aluetiheyden seuraavasti:

tämä tarkoittaa, että pienen suorakulmion massa on sen pinta-alasta riippuva pikkuruinen arvo (DM).

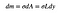
lopuksi minun täytyy saada L Y: n suhteen. teen sen siten, että saan ensin lausekkeen X: n suhteen. Voin kutsua suorakulmion vasenta puolta ” x ”ja oikeaa puolta”s”. Tämä tarkoittaa, että:

mutta kyseisen kolmion vasenta puolta voidaan kuvata Jana yhtälöllä:

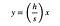
missä (h/S) on rinne. Voin ratkaista yhtälön x: lle ja korvata sen lausekkeella L.

miten olisi nopea todellisuuden tarkistus. Varmistetaan, että homma toimii, ennen kuin mennään liian pitkälle. Mitä jos annamme y = h? Että pitäisi olla yläosassa kolmion, jonka suorakulmion pituus on nolla. Jep. Se toimii. Entä y = 0? Suorakulmion pitäisi olla pituus s. näyttää hyvältä.

nyt pitää vain laittaa kaikki nämä jutut kasaan. Tämä on suorakulmion siivun massa.

”s” kumoaa FTW: n (voitolle).

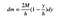
se riittää toistaiseksi. Seuraava askel on kirjoittaa lauseke y-massakeskukselle. Koska annan tämän kappaleen leveyden mennä nollaan, saan summan sijaan integraalin.

voin integroida tämän, mutta on helpompaa, jos hajotan sen kahteen osaan. Vain vähän algebraa antaa minulle:

nyt voin integroitua. Tämän minä saan.

rajojen arviointi (mikä on helppoa, koska alaraja on nolla):

boom. Se on y-massakeskus. Se on jopa yksiköt etäisyys (joka sen pitäisi). Huomaa myös, että Y-massakeskiö ei riipu kolmion pituudesta X-suunnassa (parametri s). Ei se mitään. Se tarkoittaa myös, että voimme helposti löytää X-massakeskiön. Minun tarvitsee vain rikkoa sama kolmio pystysuoriksi suorakulmioiksi.

jotta matematiikka olisi sama x-suunnassa, joudun siirtämään Origon kolmion toiseen kulmaan. Tämä tarkoittaa, että x-massakeskiö on (1/3) s oikealta puolelta. Näin saadaan kokonaismassa:

Cool.

massakeskipisteen numeerinen laskeminen

Oh, luulitko, että olin valmis? En lopettanut vielä. Miten olisi tämä-massakeskiön numeerinen laskeminen? Siitä tulee hauskaa. Tässä on suunnitelmani.

• valitse kolmion todelliset mitat. En voi laskea muuttujia numeerisesti. Tarvitsen numeroita. Käytän S = 4, h=1. Kyllä, pitäisi olla yksiköitä, mutta sillä ei ole väliä. OK, alueen tiheys on 1 (pitäisi olla selvää, että myös ei ole väliä).
• valitse pieni askelkoko. Sanotaan, että minulla on pieniä palikoita, joiden koko on 0,01 X 0,01. Etsi vektorin sijainti tämän lohkon ja sen massa (kaikki lohkot on sama massa).
• käytä massakeskipisteen summakaavaversiota.
• siirrä lohkoa eteenpäin, kunnes kolmion kaikki osat on peitetty.

tehdään näin. On pieni ongelma. Minun täytyy tehdä silmukka silmukan sisällä. Sisempi silmukka laskee X-akselin suuntaisia neliöitä vasemmasta rinteestä x = h: hon. ulompi silmukka liikuttaa näitä vaakasuoria rivejä ylöspäin 0: sta h: hon.

tässä on koodin pääosa (täysi koodi tässä):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

palan koko on 0,01 by 0,01, saan seuraavan:

joo, I olen aika tyytyväinen siihen.