miten muistat paikan autiolla saarella, jonne hautasit aarteesi? Valitse maamerkki, sano palmu, ja mittaa, kuinka monta askelta pohjoiseen / etelään ja kuinka monta askelta itään/länteen sinun täytyy mennä, että maamerkki päästä aarre. Ajatus on yksinkertainen, mutta yllättäen matemaatikoilta kesti vuosisatoja kehittää sen koko potentiaali omalla alallaan. Kun he lopulta tekivät, se mullisti matematiikan tuomalla yhteen kaksi aluetta, joilla on päällisin puolin vähän tekemistä toistensa kanssa: algebra ja geometria.
kun alamme opiskella geometriaa, ajattelemme yleensä yksinkertaisia muotoja, kuten viivoja, kolmioita ja ympyröitä kaksiulotteisessa tasossa. Voit rakentaa näitä ja monimutkaisempia muotoja viivoittimella, kompassit ja astelevy. Antiikin kreikkalaiset olivat mestareita tämäntyyppisessä geometriassa: käyttämällä vain kompassit ja straight-edge (merkitsemätön hallitsija) he pystyivät rakentamaan erilaisia muotoja ja he voisivat jopa todistaa matemaattisia tuloksia, kuten Pythagoras lause, käyttämällä näitä yksinkertaisia työkaluja.
on kuitenkin tiettyjä asioita, joita ei voi tehdä näitä perusmenetelmiä käyttäen. Kaksi muotoa, vaikkapa viiva ja ympyrä, voivat leikkautua tai olla leikkaamatta, ja ne voivat leikkautua eri tavoin: ehkä linja vain koskettaa ympyrää, ehkä se ajaa pienen kaaren pois siitä, tai ehkä se leikkaa sen kahtia. Tallentaa nämä tiedot tarvitset tapa kuvata sijainnit muotoja.
tässä kohtaa Aarresaari-idea tulee hyödylliseksi. Se havainnollistaa niin sanottua Karteesista koordinaatistoa. Valitse tasossa oleva piste, jota kutsutaan origoksi, ja piirrä sen läpi kaksi kohtisuoraa akselia, yksi vaaka-ja yksi pystysuora. Mikä tahansa tason piste voidaan saavuttaa origosta kulkemalla tietty etäisyys \(x\) vaaka-akselia pitkin ja tietty etäisyys \(y\) pystyakselia pitkin. Numerot \((x, y)\) ovat pisteen koordinaatteja. Origolla itsessään on koordinaatit \((0,0)\). Vaaka-akselin osa (jota kutsutaan myös \(x\)-akseliksi), joka sijaitsee Origon vasemmalla puolella, ja pystyakselin osa (\(y\) – akseli) Origon alapuolella kuvataan negatiivisilla luvuilla.
karteesiset koordinaatit on nimetty 1600-luvun ranskalaisen filosofin ja matemaatikon René Descartesin mukaan. On olemassa (luultavasti perätön) tarina, että Descartes keksi nämä koordinaatit maatessaan sängyssä katsellen kärpästä katossa ja miettien, miten kuvailla sen sijaintia. Descartesin mieltymys siihen, että hän makasi vuoteessa puoleenpäivään asti, saattoi itse asiassa olla syynä hänen kuolemaansa, joka tapahtui Tukholmassa vuonna 1650. Descartes oli Ruotsissa toimimassa matematiikan opettajana kuningatar Kristiinalle, joka Valitettavasti halusi työskennellä aikaisin aamulla. Joidenkin tietojen mukaan juuri nämä varhaiset tunnit ja Skandinavian lämpötilat aiheuttivat keuhkokuumeen, joka lopulta tappoi hänet. Toiset ovat esittäneet, että hänet myrkytti katolinen pappi, joka oli huolissaan Descartesin radikaalista teologiasta.
kummassakin tapauksessa Karteesinen koordinaatisto on yksi Descartesin tärkeimmistä perimätiedoista (tosin hän ei ollut ainoa, jolla idea oli). Sen avulla voidaan vastata geometrisiin ongelmiin algebran avulla ja visualisoida algebrallisia suhteita, jotka muuten jäisivät melko abstrakteiksi. Otetaan esimerkiksi yhtälö \ voimme piirtää tämän funktion kuvaajan Karteesisessa koordinaatistossa piirtämällä kaikki pisteet, joiden koordinaatit ovat muotoa \((x, 2x-1)\): pisteitä kuten \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), ja \((1.73, 2.46)\). Tällöin kuvaaja on suora, joka täyttää \(y\)-akselin pisteessä \((0,-1)\) ja jonka kaltevuus on \(2\).
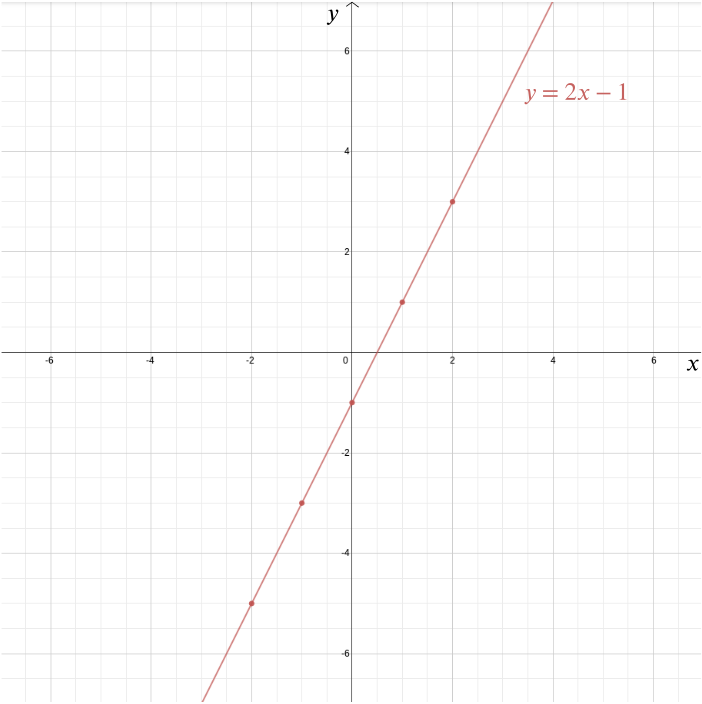
yleisemmin jokainen suora saadaan yhtälöllä muodossa\, jossa \(M\) antaa suoran kaltevuuden ja \((0, b)\) on piste, jossa se leikkaa \(y\)-akselin. Pystyviiva, joka ei ylitä \(y\)-akselia, saadaan yhtälöllä muodossa \(x=c\). Tällöin \((c, 0)\) on piste, jossa se leikkaa \(x\)-akselin.
entä ympyrä? Ympyrä koostuu kaikista niistä pisteistä, jotka ovat yhtä kaukana \(r\) annetusta pisteestä \(m\). Oletetaan, että \(M\) on piste \((0,0)\). Pythagoraan lauseesta tiedämme, että jos piste \((x, y)\) sijaitsee etäisyydellä \(r\) kohteesta \((0,0)\), niin \
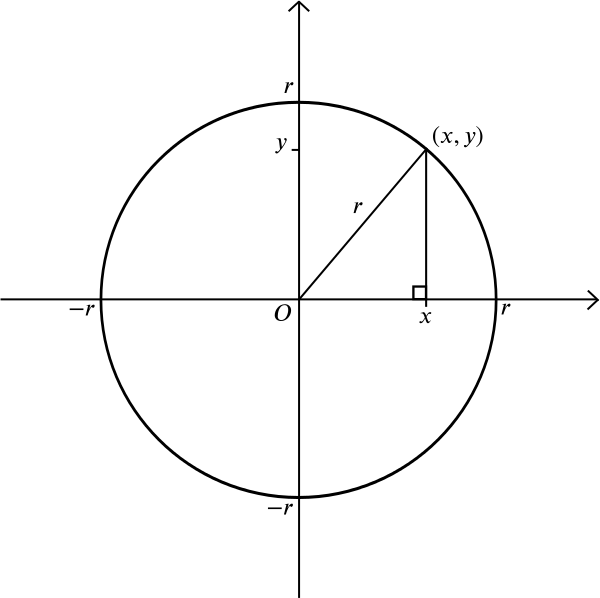
Tämä on siis yhtälö, jossa ympyrän säde \(r\) keskittyy origoon. Voit selvittää itse, että ympyrän säde \(r\) keskitetty piste \((a,b)\) on yhtälö \, mutta tässä on monimutkaisempi kysymys: minkä muodon saa, kun ottaa huomioon kaikki pisteet, jotka sijaitsevat yhtä kaukana annetusta pisteestä ja annetusta suorasta? Ilman koordinaattijärjestelmää voisi piirtää pisteen ja janan ja kokeilla viivoitinta tai kompasseja. Voisit piirtää muutaman pisteen, jotka sijaitsevat yhtä kaukana molemmista ja katso, jos voit arvata yleinen muoto.
koordinaatistolla varustettuna vastaus muuttuu kuitenkin paljon helpommaksi ja paljon tarkemmaksi. Oletetaan, että annettu piste on etäisyydellä \(1\) annetusta suorasta. Sijoitetaan annettu piste origoon ja annettu suora niin, että se on vaakasuora,Pythagoraan lauseen yhtälön \ avulla minkä tahansa pisteen \((x, y)\) etäisyys \((0,0)\) on \(\sqrt{x^2 + y^2}\). Etäisyys pisteestä \((x, y)\) suoralle \(y = -1\) on \(|y+1|\) (käytämme tässä itseisarvoa, koska \(y\)-koordinaatti saattaa olla negatiivinen). Jos nämä kaksi ovat yhtäsuuret, niin \ Neliöiminen kummaltakin puolelta antaa \ järjestely antaa \ niin mikä tahansa piste, joka on yhtä kaukana pisteestä \((0,0)\) ja suoralla \(y=-1\) on koordinaatit \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Voit tarkistaa itse, että myös käänteisluku on totta: jokainen piste näillä koordinaateilla sijaitsee yhtä kaukana pisteestä \((0,0)\) ja suorasta \(y=-1\).
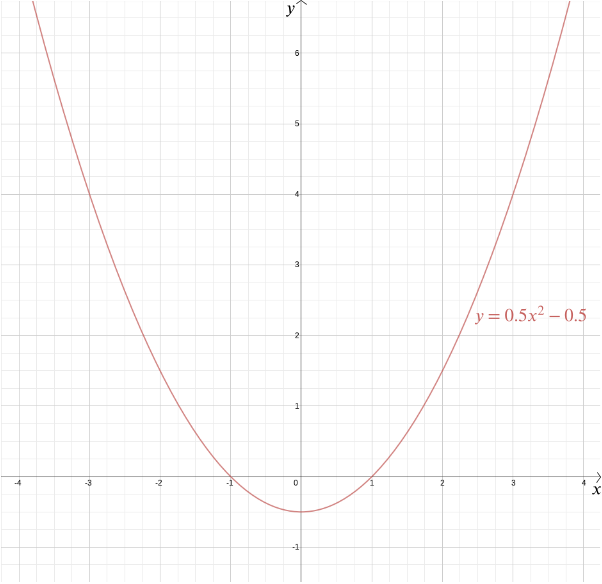
voimme piirtää tämän funktion kuvaajan nähdäksemme vaaditun muodon, joka osoittautuu paraabeliksi. Itse asiassa jokainen kvadraattinen funktio \ \(A\), \(b\) ja \(c\) vakioille antaa meille paraabelin. Tämä tuttu muoto, joka voi tulla niin monia hienovaraisia muunnelmia—pitkä ja ohut tai kyykky ja tasainen—on vangittu tämän kätevän algebrallinen ilmaus. Se, että nykyään termejä ”quadratic function” ja ”parabola” pidetään lähes synonyymeinä, korostaa Descartesin idean onnistumista. Yleisemmin mikä tahansa algebrallinen suhde kahden muuttujan \(x\) ja \(y\) välillä antaa meille käyrän, jota voimme piirtää Karteesisilla koordinaateilla.
algebrallisen esityksen avulla on helppo vastata lukuisiin geometrisiin kysymyksiin. Selvittääksemme\: n ja paraabelin \(y = \frac{x^2}{2} – \frac{1}{2}\) antaman suoran leikkauspisteet toteamme yksinkertaisesti, että \(y\) minkä tahansa pisteen \((x,y)\) koordinaatin, joka sijaitsee molemmissa, on täytettävä molemmat yhtälöt, joten \ tämä antaa \ ratkomalla neliöyhtälön saamme \ ja \ niin leikkauspisteet ovat \
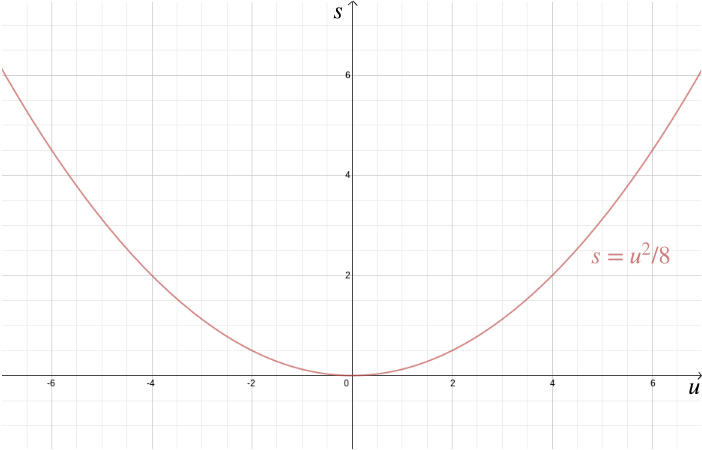
lukuun ottamatta geometristen ongelmien ratkaisemista, karteesiset koordinaatit auttavat myös algebrallisten suhteiden visualisoinnissa. Oletetaan esimerkiksi, että auto kulkee nopeudella \(u\) ja kuljettaja jarruttaa, jolloin hidastuvuus on jatkuvasti esimerkiksi \(-4\) metriä/sekunti\(^2\). Pysähtymismatka \(s\)—matka, jonka auto peittää ennen pysähtymistä—saadaan algebrallisesta suhteesta\, jossa tämä merkitään Karteesisilla koordinaateilla, selviää, kuinka tärkeää on hidastaa kaupunkialueilla, koska pysähtymismatka kasvaa nopeasti \(u\).
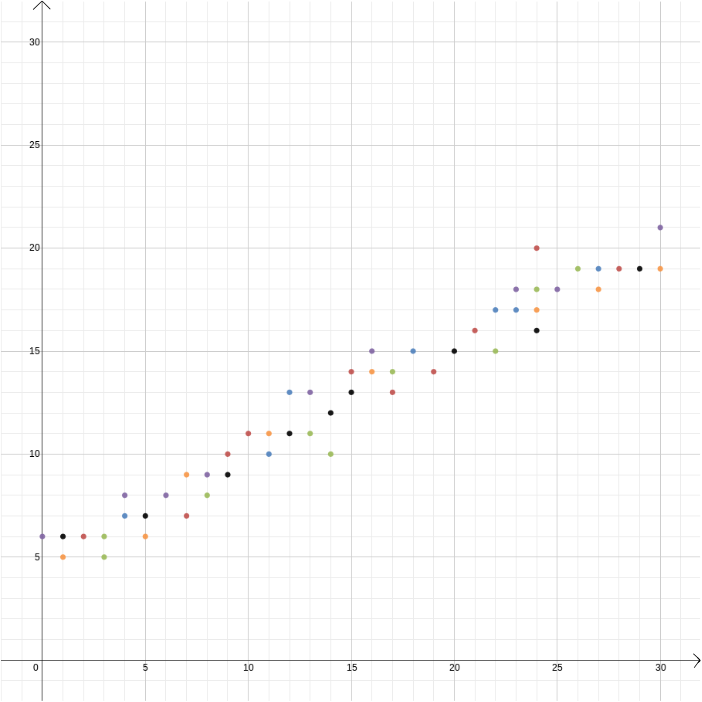
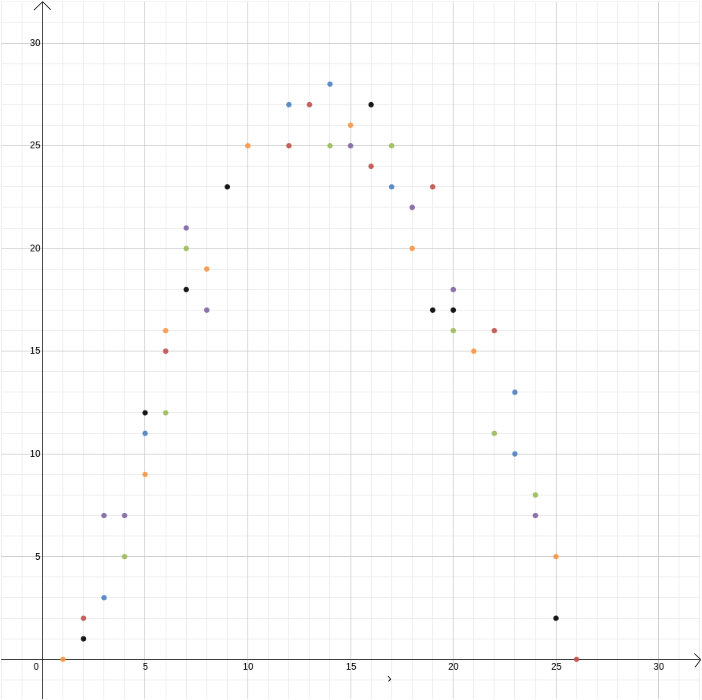
tässä esimerkissä tunsimme kahden muuttujan välisen suhteen, koska se voidaan johtaa fysiikan laeista. Karteesisista koordinaateista on hyötyä myös silloin, kun epäilee kahden muuttujan liittyvän toisiinsa, mutta ei tiedä miten. Oletetaan, että jäätelömyyjän saaman voiton ja ulkolämpötilan välillä on yhteys. Selvittääksemme, mikä tämä suhde voisi olla, voimme mitata lämpötilan ja voiton vaikkapa vuoden aikana ja piirtää arvot toisiaan vastaan, jolloin lämpötila kirjataan \(x\) – akselille ja voitto \(y\)-akselille. Sen jälkeen katsotaan, havaitsemmeko kuvion. Ensimmäisessä kaaviossa alla saatamme arvata, että suhde on lineaarinen, ja voimme yrittää löytää suoran \ joka parhaiten sopii meidän tiedot (on olemassa menetelmiä löytää tämä parhaiten sovi). Alla olevassa toisessa kaaviossa saatamme arvata, että suhde on neliömäinen ja jälleen voimme yrittää löytää funktion\, joka parhaiten sopii dataan.
Karteesisilla koordinaateilla oli suuri merkitys laskennan kehityksessä 1600-luvun jälkipuoliskolla. Calculus mahdollistaa käyrien attribuuttien, kuten niiden kaltevuuden tietyssä pisteessä tai alueen alueen, joka sijaitsee käyrän ja \(x\)-akselin välissä. Näilläkin voi olla fyysisiä tulkintoja. Jos esimerkiksi kuvaamme matkan, jonka auto kulkee kulkuaikaa vastaan, tuloksena olevan käyrän kaltevuus tiettynä aikana—etäisyyden muutosnopeus suhteessa aikaan—kuvaa nopeutta, jolla auto kulki kyseisenä ajankohtana: se on funktion derivaatta, joka antaa meille matkan ajan suhteen. Katso myös miksi kaltevuudet ovat tärkeitä reaalimaailmassa?.
voimme myös nousta ulottuvuuteen tarkastelemalla kolmatta akselia, joka on kohtisuorassa kahteen ensimmäiseen nähden, minkä voi kuvitella tulevan paperiarkistasi ja osoittavan sinua. Käyttämällä tällaista kolmiulotteista järjestelmää voit nyt esittää kolmiulotteisia objekteja ja visualisoida, miten kolmas muuttuja \(z\) riippuu kahdesta ensimmäisestä, \(x\) ja \(y\).
näiden esimerkkien pitäisi antaa sinulle jonkinlaisen käsityksen siitä, miksi koordinaateista on tullut niin välttämättömiä kaikilla tieteen aloilla fysiikasta tähtitieteeseen ja tekniikkaan, ja myös kuvateollisuudessa tuottamaan tietokonegrafiikkaa ja tietokoneella luotua kuvastoa, jota ihailemme elokuvissa ja peleissä.
itse matematiikassa algebran ja geometrian välinen yhteys on kulminoitunut kokonaisuuteen nimeltä algebrallinen geometria, jolla on oma kiehtovuutensa. Ehkä tunnetuin tällä alueella syntynyt tulos on Fermat ’n suuri lause, joka on nimetty Descartesin aikalaisen Pierre de Fermat’ n mukaan, joka myös vaikutti merkittävästi karteesisen koordinaatiston kehitykseen. Fermat ’ n pohdinnassa oli kysymys, joka yhdistää geometrian lukuteoriaan. Pythagoraan lauseen mukaan jos \(A\), \(b\) ja \(C\) ovat suorakulmaisen kolmion sivut ja \(C\) on oikean kulman vastakohta, niin \(a^2 + b^2 = C^2\). On äärettömän monta triplettiä kokonaislukuja \(A\), \(b\) ja \(c\), jotka täyttävät tämän suhteen; \((3,4,5)\) on esimerkki.
oletetaan nyt, että muutetaan eksponenttia ja tarkastellaan lausekkeita kuten \ ja \ ja yleisemmin\, missä \(n\) on luonnollinen luku suurempi kuin \(2\). Voimmeko silti löytää positiivisia kokonaislukuja \(A\), \(b\) ja \(c\) täyttävän yhtälön? Fermat ’ n epäillään, että emme voi ja hän raapustettu niin paljon marginaali hänen matematiikan tekstikirjan, sanomalla, että hän oli ”ihmeellinen todiste”, että se, joka marginaali oli liian kapea sisältää.
tuon töherryksen piti kummitella matemaatikoille yli 350 vuotta. Se oli vasta 1994, että oikea todiste tästä näennäisesti harmiton tulos oli lopulta ilmoitti matemaatikko Andrew Wiles. Wiles oli käyttänyt laajasti algebrallista geometriaa. Erityisesti hän oli käyttänyt tuloksia koskevat ellipsinmuotoinen käyriä kuvattu kohtia plane, jonka koordinaatit täyttävät \ Descartes ” contemplation, lentää on tullut pitkän matkan!
