cesàron summaus

admin

on olemassa useampi kuin yksi tapa summata ääretön sarja. Cesàron summauksen avulla voi laskea niiden sarjojen summan, joilla ei ole summaa klassisessa mielessä.

Oletetaan, että meillä on ääretön sarja

a_0 + a_1 + a_2 + \cdots

sarjan n.osasumma on annettu

S_n = \sum_{i=0}^n a_i

sarjan klassinen summa, jos se on olemassa, määritellään sen osasummien rajaksi. Toisin sanoen

\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\to\infty} \sum_{i=0}^n a_i

Cesàron yhteenlaskussa noudatetaan erilaista lähestymistapaa. Sen sijaan, että otettaisiin osasummien raja, otetaan osasummien keskiarvojen raja. Tarkentaaksesi määrittele

C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}

ja määrittele cesàron yhteenlasku Cn: n rajaksi, kun n menee äärettömyyteen. Jos sarjalla on summa klassisessa merkityksessä, sillä on summa myös Cesàron merkityksessä, ja rajat ovat samat. Joissakin sarjoissa on kuitenkin cesàron summa, jossa ei ole klassista summaa. Tai ehkä molemmat rajat ovat olemassa, mutta välivaiheet cesàro summaus ovat paremmin käyttäytyviä, kuten näemme alla olevassa esimerkissä.

Jos ilmaiset Cn: n alkuperäisen an termin mukaan, saat

c_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i

toisin sanoen, nth cesàron osasumma on klassisen osasumman uudelleenpainotus, jossa painot muuttuvat n: n funktiona. murtoluvun kertominen ai menee 1: een n: n kasvaessa.

Fejérin yhteenlasku ja Gibbsin ilmiö

Fejérin yhteenlasku on Cesàron yhteenlasku, jota sovelletaan Fourier ’ n sarjaan. Fourier ’ n sarjan (tavalliset) osittaissummat antavat parhaan likiarvon funktiolle mitattuna pienimmän neliösumman normilla. Cesàron osittaissummat voivat kuitenkin kvalitatiivisesti muistuttaa enemmän approksimoitavaa funktiota. Osoitamme tämän alla neliöaallolla.

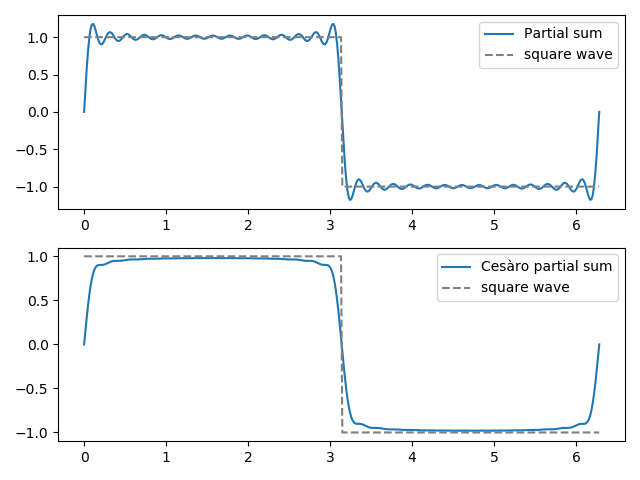
30.tavallinen osasumma näyttää Gibbsin ilmiön alun, ”lepakkokorvat” neliöaallon yläosassa ja niiden peilikuvan alareunassa. 30. cesàron osittaissumma on tasaisempi ja eliminoi Gibbs-ilmiöt lähellä epäjatkuvuutta neliöaallossa.

lisää Fourier-sarjan viestejä

  • Fourier-Besselin sarja
  • vastaesimerkki Dirichlet ’ n periaatteelle
  • leikatut siniaallot

Vastaa

Sähköpostiosoitettasi ei julkaista.