Hay más de una forma de sumar una serie infinita. La suma de Cesàro le permite calcular la suma de series que no tienen suma en el sentido clásico.
Supongamos que tenemos una serie infinita
La enésima suma parcial de la serie viene dada por
La suma clásica de la serie, si existe, se define como el límite de sus sumas parciales. Es decir,
Cesàro suma adopta un enfoque diferente. En lugar de tomar el límite de las sumas parciales, toma el límite de los promedios de las sumas parciales. Para ser específico, defina
y defina la suma de Cesàro como el límite del Cn cuando n va al infinito. Si una serie tiene una suma en el sentido clásico, también tiene una suma en el Cesàro sentido, y los límites son los mismos. Pero algunas series tienen una suma Cesàro que no tienen una suma clásica. O tal vez ambos límites existen, pero los pasos intermedios de la suma de Cesàro se comportan mejor, como veremos en un ejemplo a continuación.
Si expresa el Cn en términos de los términos an originales, obtiene
En otras palabras, la suma parcial enésima de Cesàro es una re-ponderación de las sumas parciales clásicas, con los pesos cambiando en función de n. Tenga en cuenta que para i fijo, la fracción que multiplica ai va a 1 a medida que aumenta n.
La suma de Fejér y el fenómeno de Gibbs
La suma de Fejér es la suma de Cesàro aplicada a la serie de Fourier. Las sumas parciales (ordinarias) de una serie de Fourier dan la mejor aproximación a una función medida por la norma de mínimos cuadrados. Pero las sumas parciales de Cesàro pueden ser cualitativamente más parecidas a la función que se aproxima. Demostramos esto a continuación con una onda cuadrada.
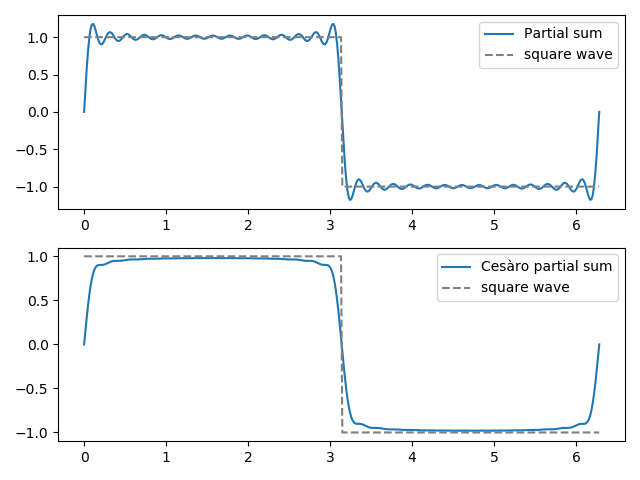
La suma parcial ordinaria número 30 muestra los inicios del fenómeno de Gibbs, las «orejas de murciélago» en la parte superior de la onda cuadrada y su imagen especular en la parte inferior. La suma parcial de Cesàro número 30 es más suave y elimina los fenómenos de Gibbs cerca de la discontinuidad en la onda cuadrada.
Más publicaciones de la serie de Fourier
- Serie de Fourier-Bessel
- Contraejemplo al principio de Dirichlet
- Ondas sinusoidales recortadas
