Vamos a hacer esto. Voy a derivar la expresión para el centro de masa para un triángulo rectángulo. ¿Por qué?

a Ver, vamos a tener diversión. Ya he incluido un meme de Yoda. ¿Qué podría salir mal?

Aquí está el triángulo.

Oh, se ve como un triángulo azul. ¿Verdad? Pero supongamos que se trata de una lámina de metal delgada con una masa de M. ¿Cómo encontrarías la ubicación del centro de masa? Comencemos con la definición básica de centro de masa.

Este es esencialmente un promedio ponderado. OK, ES un promedio ponderado. Pero si rompes el objeto en un montón de pequeñas piezas, entonces multiplica la posición vectorial de cada masa y su pequeña masa. Luego se suma todo y se divide por la masa total. Ese es el centro de masa. Aquí hay otra foto.

Por supuesto, en este caso no tenemos un montón de piezas. Tenemos una masa continua. Eso significa que podemos convertir la suma en una integral. En lugar de tratar con las direcciones x e y al mismo tiempo, voy a considerar el centro de masa y.

Empezaré dividiendo este triángulo en un montón de rectángulos horizontales. Aquí está uno de esos rectángulos.

Así, Puedo usar estos flaco rectángulos para encontrar el centro de masa. Solo necesito multiplicar la posición de cada rectángulo y la masa de cada rectángulo. La posición es bastante sencilla, es «y». La masa es un poco más complicada. Además, observe que para los rectángulos que se mueven hacia arriba en el triángulo, son más pequeños con una masa más pequeña.

El área de este pequeño rectángulo debe ser proporcional a su área. Permítanme definir la densidad de área de todo triángulo como:

eso significa Que la masa de la pequeña rectángulo será el pequeño valor (dm) que depende de su área.

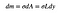
por último, necesito L en términos de y. Voy a hacer que por primera vez una expresión en términos de x. Puedo llamar al lado izquierdo del rectángulo «x «y al lado derecho»s». Esto significa que:

Pero el lado izquierdo de ese triángulo que puede ser descrito como una línea con la ecuación:

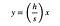
Donde (h/s) es la pendiente. Puedo resolver esta ecuación para x y sustituir en la expresión para L.

¿qué tal una rápida verificación de la realidad. Asegurémonos de que las cosas funcionen antes de ir demasiado lejos. ¿Y si dejamos y = h? Que debe estar en la parte superior del triángulo con una longitud de rectángulo de cero. Sip. Eso funciona. ¿Y y = 0 ? El rectángulo debe tener una longitud de s. Se ve bien.

Ahora solo necesito juntar todo esto. Esta es la masa de esa rebanada de un rectángulo.

La «s» cancela FTW (por la victoria).

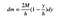
Eso es suficiente por ahora. El siguiente paso es escribir una expresión para el centro de masa y. Ya que voy a dejar que el ancho de esta pieza vaya a cero, voy a obtener una integral en lugar de una suma.

me puede integrar este, pero es más fácil si se me rompe en dos partes. Sólo un poco de álgebra me da:

Ahora que me pueda integrar. Esto es lo que obtengo.

la Evaluación en los límites (que es fácil, ya que el límite inferior es cero):

Boom. Ese es el centro y de masa. Incluso tiene unidades de distancia (que debería). Además, observe que el centro de masa y no depende de la longitud del triángulo en la dirección x (el parámetro s). Eso es genial. También significa que podemos encontrar fácilmente el centro de masa x. Todo lo que necesito hacer es romper ese mismo triángulo en rectángulos verticales.

Con el fin de hacer la matemática de la misma en la dirección x, yo sería necesario para mover el origen de la otra esquina del triángulo. Esto significa que el centro de masa x es (1/3) s desde el lado derecho. Esto da un total de centro de masa de:

Fresco.

Cálculo numérico del Centro de Masa

Oh, ¿pensaste que había terminado? No he terminado. ¿Qué tal esto – un cálculo numérico del centro de masa? Sí, será divertido. Este es mi plan.

• Elija las dimensiones reales de un triángulo. No puedo hacer un cálculo numérico con variables. Necesito números. Voy a usar s = 4, h=1. Sí, debería haber unidades, pero no importará. OK, la densidad del área es 1 (debe quedar claro que tampoco importa).
• Elige un tamaño de paso pequeño. Digamos que tengo bloques pequeños con un tamaño de 0.01 por 0.01. Encuentra la ubicación vectorial de este bloque y su masa (todos los bloques tienen la misma masa).
• Utilice la versión de fórmula de suma del centro de masa.
• Mueva el bloque hasta que todas las partes del triángulo estén cubiertas.

Hagamos esto. OK, hay una pequeña dificultad. Voy a necesitar hacer un bucle dentro de un bucle. El bucle interno se suman los cuadrados a lo largo del eje x desde la izquierda pendiente para x = h. El bucle externo será el movimiento de estas filas horizontales de hasta de 0 a h.

esta es la parte principal del código (código completo aquí):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

Con un tamaño de la pieza de 0,01 0,01, me sale lo siguiente:

Sí, estoy bastante contento con eso.