¿Cómo recuerdas el lugar en una isla desierta donde enterraste tu tesoro? Elige un punto de referencia, diga una palmera y mida cuántos pasos norte / sur y cuántos pasos este/oeste tiene que ir desde ese punto de referencia para llegar al tesoro. Es una idea simple, pero, sorprendentemente, los matemáticos tardaron siglos en desarrollar todo su potencial en su propio campo. Cuando finalmente lo hicieron, revolucionó las matemáticas al reunir dos áreas que a primera vista tienen poco que ver entre sí: álgebra y geometría.
Cuando empezamos a aprender geometría, generalmente pensamos en formas simples como líneas, triángulos y círculos en el plano bidimensional. Puede construir estas y otras formas más complicadas utilizando una regla, un compás y un transportador. Los antiguos griegos eran maestros en este tipo de geometría: usando solo brújulas y un borde recto (una regla sin marcar), fueron capaces de construir una gama de formas e incluso pudieron probar resultados matemáticos, como el teorema de Pitágoras, utilizando estas herramientas simples.
Sin embargo, hay ciertas cosas que no puedes hacer usando estos métodos básicos. Dos formas, digamos una línea y un círculo, pueden o no cruzarse, y pueden cruzarse de diferentes maneras: tal vez la línea solo toque el círculo, tal vez afeite un pequeño arco o tal vez lo corte por la mitad. Para registrar esta información, necesita una forma de describir las ubicaciones de las formas.
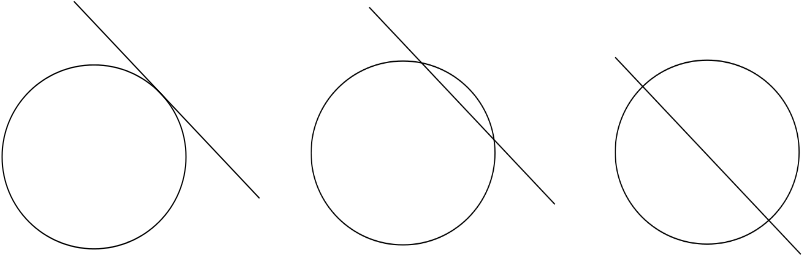
Aquí es donde la idea de la isla del tesoro es útil. Ilustra lo que se llama el sistema de coordenadas cartesianas. Elija un punto en el plano, llamado el origen, y dibuje dos ejes perpendiculares a través de él, uno horizontal y otro vertical. Se puede llegar a cualquier punto del plano desde el origen recorriendo una cierta distancia \(x\) a lo largo del eje horizontal y una cierta distancia \(y\) a lo largo del eje vertical. Los números \((x, y)\) son las coordenadas del punto. El origen en sí tiene coordenadas \((0,0)\). La parte del eje horizontal(también llamada eje \(x\)) que se encuentra a la izquierda del origen y la parte del eje vertical (el eje \(y\)) debajo del origen se describen con números negativos.
Las coordenadas cartesianas llevan el nombre del filósofo y matemático francés del siglo XVII René Descartes. Hay una historia (probablemente falsa) de que Descartes inventó estas coordenadas mientras estaba acostado en la cama viendo una mosca en el techo y preguntándose cómo describir su ubicación. La inclinación de Descartes por acostarse en la cama hasta el mediodía puede haber sido la causa de su fallecimiento, que ocurrió en Estocolmo en 1650. Descartes estaba en Suecia para actuar como tutor de matemáticas de la reina Cristina, quien desafortunadamente prefirió trabajar temprano en la mañana. Según algunos informes, fueron estas primeras horas y las temperaturas escandinavas las que causaron la neumonía que finalmente lo mató. Otros han sugerido que fue envenenado por un sacerdote católico preocupado por la teología radical de Descartes.
De cualquier manera, el sistema de coordenadas cartesianas es uno de los legados más importantes de Descartes (aunque no fue la única persona que tuvo la idea). Nos permite responder a problemas geométricos usando álgebra y visualizar relaciones algebraicas que de otra manera permanecerían bastante abstractas. Tomemos por ejemplo la ecuación \ Podemos trazar el gráfico de esta función en un sistema de coordenadas cartesianas trazando todos los puntos cuyas coordenadas sean de la forma \((x, 2x-1)\): puntos tales como \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), y \((1.73, 2.46)\). En este caso, el gráfico es una línea recta que cumple con el eje \(y\) en el punto \((0,-1)\) y tiene una pendiente de \(2\).
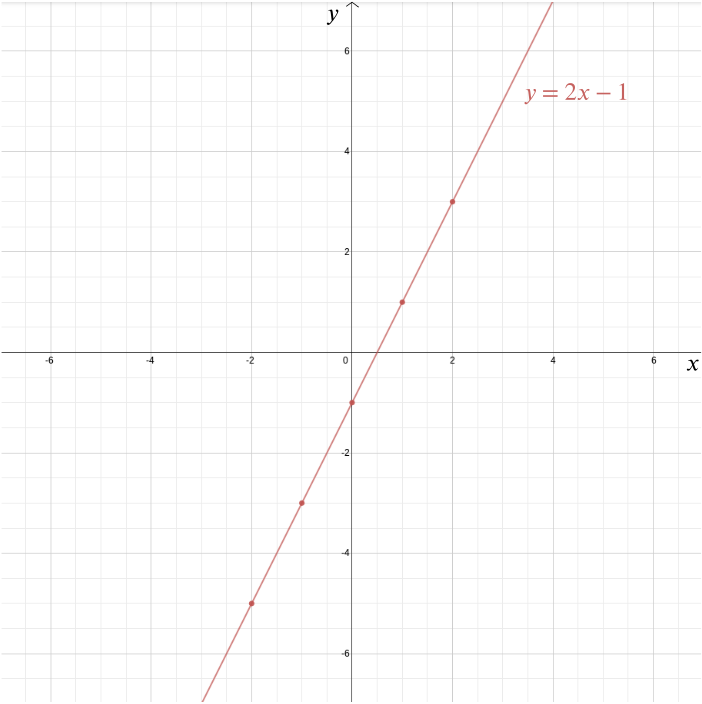
Más generalmente cada línea recta está dada por una ecuación de la forma \, donde \(m\) le da la pendiente de la recta y \((0,b)\) es el punto en que se cruza el \(y\)-eje. Una recta vertical que no cruza el eje \(y\) viene dada por una ecuación de la forma \(x=c\). En este caso, \((c, 0)\) es el punto en el que cruza el eje \(x\).
¿Qué hay de un círculo? Un círculo está formado por todos aquellos puntos que se encuentran a la misma distancia \(r\) de un punto dado \(m\). Supongamos que \(m\) es el punto \((0,0)\). Por el teorema de Pitágoras sabemos que si un punto \((x, y)\) se encuentra a una distancia \(r\) de \((0,0)\), entonces \
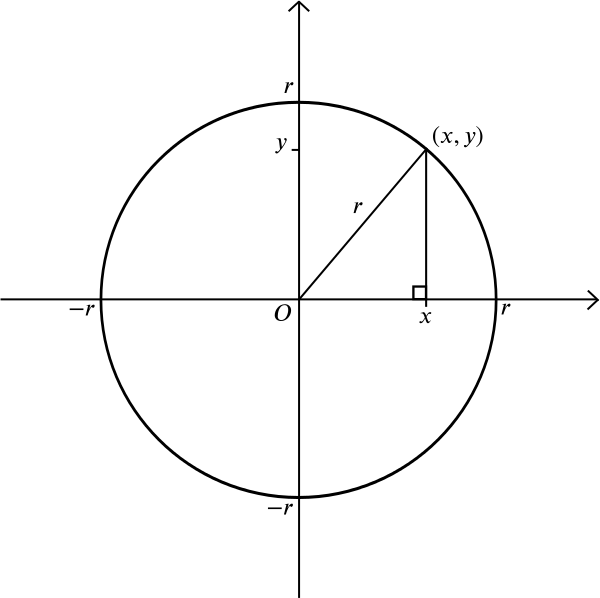
Por lo tanto, esta es la ecuación de un círculo de radio \(r\) centrado en el origen. Puede averiguar por sí mismo que un círculo de radio \(r\) centrado en el punto \((a,b)\) tiene la ecuación \, pero aquí hay una pregunta más complicada: ¿qué forma obtienes cuando consideras todos los puntos que se encuentran a la misma distancia de un punto dado y una línea dada? Sin un sistema de coordenadas, puede dibujar el punto y la línea y experimentar con su regla o brújulas. Puedes dibujar algunos puntos que se encuentran a una distancia igual de ambos y ver si puedes adivinar la forma general.
Armado con un sistema de coordenadas, sin embargo, la respuesta se vuelve mucho más fácil y mucho más precisa. Supongamos que el punto dado está a una distancia \(1\) de la línea dada. Pongamos el punto dado en el origen y la recta dada de manera que sea horizontal, dada por la ecuación \ Por el teorema de Pitágoras la distancia de cualquier punto \((x,y)\) de \((0,0)\) es \(\sqrt{x^2 + y^2}\). La distancia desde un punto \((x, y)\) a la línea \(y = -1\) es \(|y+1|\) (usamos el valor absoluto aquí porque la coordenada \(y\) puede ser negativa). Si esos dos son iguales, entonces \ Cuadrar ambos lados da \ Reordenar da \ De modo que cualquier punto a igual distancia del punto \((0,0)\) y la línea \(y=-1\) tiene coordenadas \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Puede comprobar por sí mismo que lo contrario también es cierto: cada punto con estas coordenadas se encuentra a la misma distancia del punto \((0,0)\) y la línea \(y=-1\).
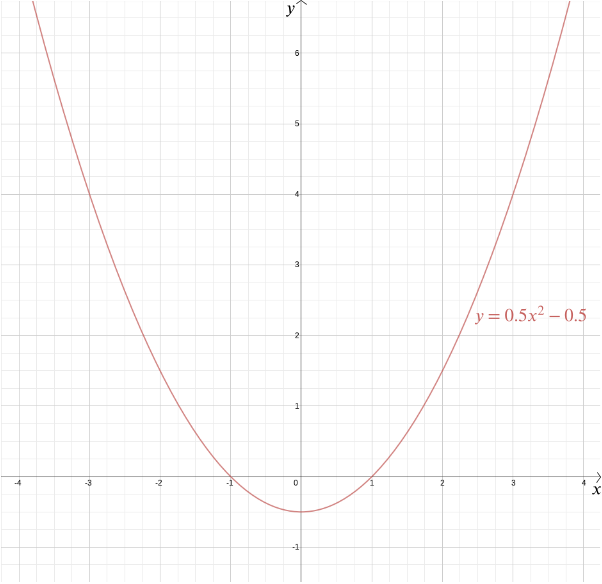
podemos trazar la gráfica de esta función para ver la forma requerida, lo cual resulta ser una parábola. De hecho, cada función cuadrática \ para constantes\ (a\),\ (b\) y\ (c\), nos da una parábola. Esta forma familiar, que puede venir en tantas variaciones sutiles, larga y delgada o en cuclillas y planas, es capturada por esta práctica expresión algebraica. El hecho de que hoy en día los términos «función cuadrática» y «parábola» se consideren casi sinónimos resalta el éxito de la idea de Descartes. De manera más general, cualquier relación algebraica entre dos variables \(x\) e \(y\) nos da una curva que podemos trazar usando coordenadas cartesianas.
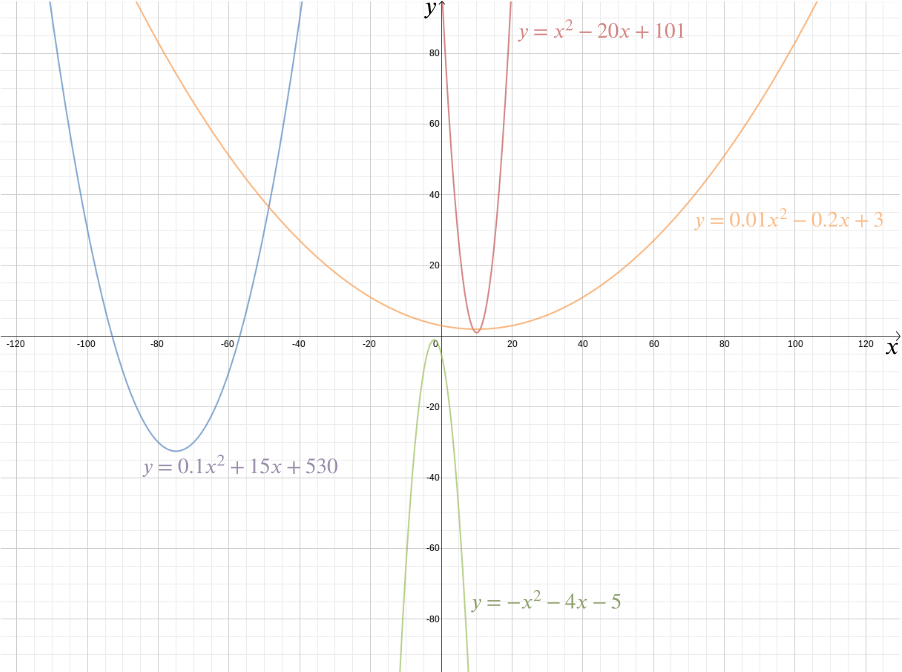
La representación algebraica facilita la respuesta a toda una gama de preguntas geométricas. Para calcular los puntos de intersección de la recta dada por \ y la parábola \(y = \frac{x^2} {2} – \frac{1} {2}\), simplemente notamos que la coordenada \(y\) de cualquier punto \((x,y)\) que se encuentra en ambos debe satisfacer ambas ecuaciones, por lo que \ Esto da \ Resolviendo la ecuación cuadrática que obtenemos \ y \ por lo que los puntos de intersección están en \
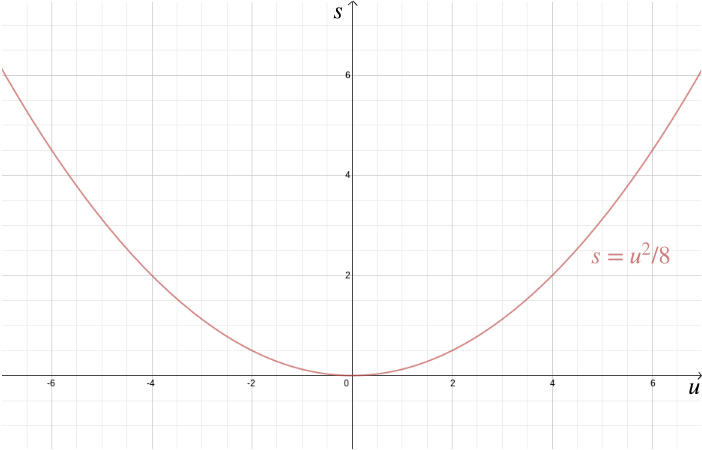
Además de resolver problemas geométricos, las coordenadas cartesianas también ayudan a visualizar relaciones algebraicas. Por ejemplo, supongamos que un automóvil viaja a la velocidad \(u\) y el conductor está aplicando los frenos, lo que resulta en una desaceleración constante de, por ejemplo, \(-4\) metros/segundos\(^2\). La distancia de parada \(s\)—la distancia que cubre el automóvil antes de que se detenga-viene dada por la relación algebraica \ Trazando esto usando coordenadas cartesianas, se muestra cuán importante es reducir la velocidad en áreas urbanas, porque la distancia de parada aumenta rápidamente con \(u\).
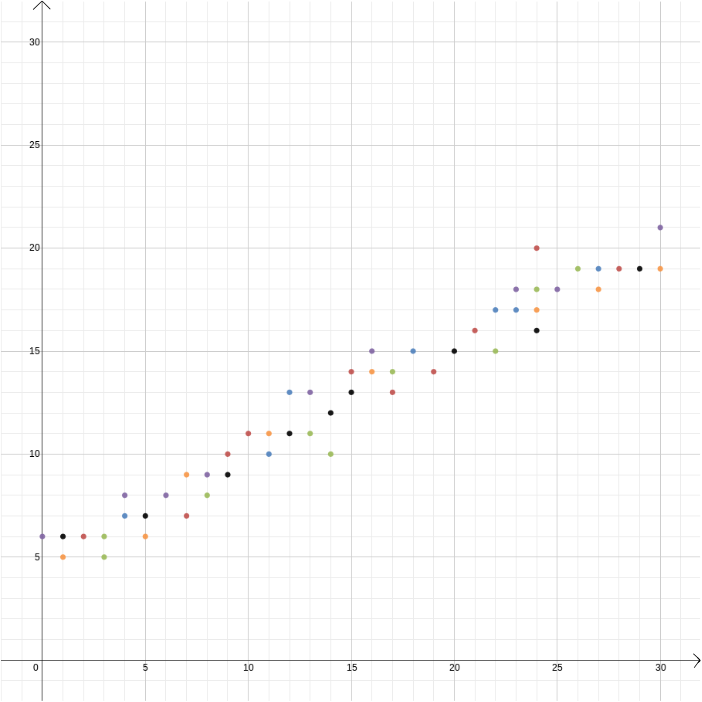
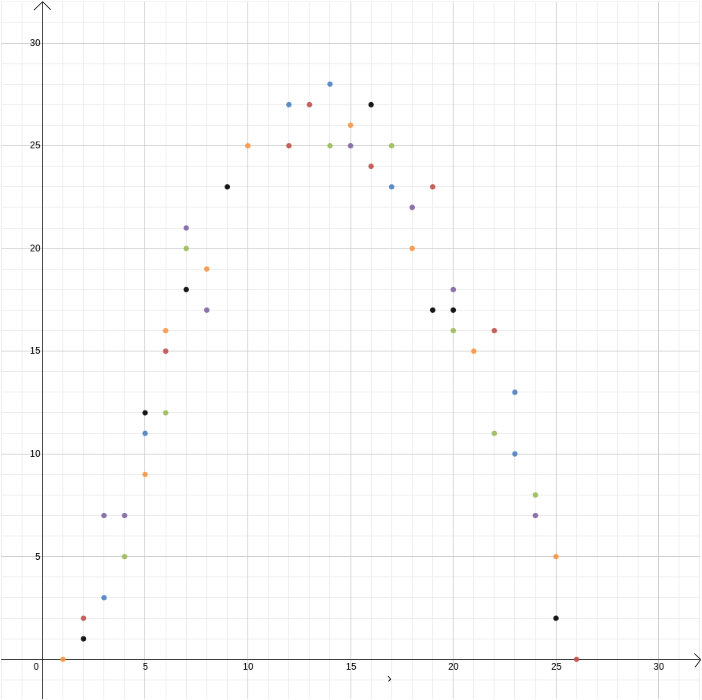
En este ejemplo conocíamos la relación entre dos variables porque puede derivarse de las leyes de la física. Pero las coordenadas cartesianas también son útiles cuando se sospecha que dos variables están relacionadas pero no se sabe cómo. Supongamos que pensamos que existe una relación entre el beneficio obtenido por un vendedor de helados y la temperatura exterior. Para averiguar cuál podría ser esa relación, podemos medir la temperatura y el beneficio durante, por ejemplo, el transcurso de un año y trazar los valores uno contra el otro, con la temperatura registrada en el eje \(x\) y el beneficio en el eje \(y\). Entonces podemos ver si podemos detectar un patrón. En el primer diagrama a continuación, podríamos adivinar que la relación es lineal, y podemos tratar de encontrar la línea recta \ que mejor se ajuste a nuestros datos (hay métodos para encontrar este mejor ajuste). En el segundo diagrama de abajo podríamos adivinar que la relación es cuadrática y de nuevo podemos intentar encontrar la función \ que mejor se ajuste a los datos.
Las coordenadas cartesianas desempeñaron un papel importante en el desarrollo del cálculo en la segunda mitad del siglo XVII. El cálculo permite calcular atributos de curvas, como su pendiente en un punto determinado o el área de la región que se encuentra entre una curva y el eje \(x\). Estos también pueden tener interpretaciones físicas. Por ejemplo, si trazamos la distancia que recorre un automóvil en relación con el tiempo que ha estado viajando, la pendiente de la curva resultante en un momento dado—la velocidad de cambio de la distancia con respecto al tiempo—representa la velocidad a la que el automóvil viajaba en ese momento en el tiempo: es la derivada de la función que nos da la distancia en términos de tiempo. Véase también ¿Por qué son importantes los gradientes en el mundo real?.
También podemos subir una dimensión considerando un tercer eje perpendicular a los dos primeros, que puedes imaginar saliendo de tu hoja de papel y apuntando hacia ti. Usando un sistema tridimensional de este tipo, ahora puede representar objetos tridimensionales y visualizar cómo una tercera variable \(z\) depende de sus dos primeras, \(x\) y \(y\).
Estos ejemplos deberían darte una idea de por qué las coordenadas se han vuelto tan indispensables en todas las áreas de la ciencia, desde la física hasta la astronomía y la ingeniería, y también en las industrias visuales para producir gráficos por computadora y las imágenes generadas por computadora que admiramos en películas y juegos.
En matemáticas, el vínculo entre álgebra y geometría ha culminado en un área entera llamada geometría algebraica, que tiene una fascinación propia. Quizás el resultado más famoso que ha surgido de esta área es el Último Teorema de Fermat, llamado así por un contemporáneo de Descartes, Pierre de Fermat, quien también contribuyó significativamente al desarrollo del sistema de coordenadas cartesianas. Fermat estaba considerando una pregunta que vincula la geometría con la teoría de números. Según Pitágoras el teorema de, si \(a\), \(b\) y \(c\) son los lados de un ángulo recto del triángulo y \(c\) es el lado opuesto al ángulo recto, entonces \(a^2 + b^2 = c^2\). Hay infinitos triples de números enteros \(a\), \(b\) y \(c\) que satisfacen esta relación; \((3,4,5)\) es un ejemplo.
Ahora supongamos que cambiamos el exponente y consideramos expresiones como \ y \ y, más generalmente, \ donde \(n\) es un número natural mayor que \(2\). ¿Todavía podemos encontrar números enteros positivos \(a\), \(b\) y \(c\) que satisfagan la ecuación? Fermat sospechó que no podíamos y garabateó tanto en el margen de su libro de texto de matemáticas, diciendo que tenía una «prueba maravillosa» de ese hecho que el margen era demasiado estrecho para contener.
Ese garabato perseguía a los matemáticos durante más de 350 años. No fue hasta 1994 que una prueba correcta de este resultado aparentemente inocuo fue finalmente anunciada por el matemático Andrew Wiles. Wiles había hecho un amplio uso de la geometría algebraica. En particular, había utilizado resultados relativos a las curvas elípticas descritas por puntos en el plano cuyas coordenadas satisfacen la contemplación de \ Descartes de una mosca que ha recorrido un largo camino!
