lad os gøre dette. Jeg vil udlede udtrykket for massens centrum for en højre trekant. Hvorfor?

se, vi skal have det sjovt. Jeg har allerede inkluderet en Yoda meme. Hvad kunne gå galt?
Her er trekanten.
åh, ligner en normal blå trekant. Ikke? Men formoder, at dette er noget tyndt metalark med en masse M. hvordan ville du finde placeringen af massecentret? Lad os starte med den grundlæggende definition af massecenter.

dette er i det væsentlige et vægtet gennemsnit. Det er et vægtet gennemsnit. Men hvis du bryder objektet i en flok små stykker, skal du multiplicere vektorpositionen for hver masse og dens lille masse. Derefter tilføjer du så alle op og dividerer med den samlede masse. Det er centrum for massen. Her er et andet billede.

I dette tilfælde har vi ikke en masse stykker. Vi har en kontinuerlig masse. Det betyder, at vi i stedet kan gøre summen til en integreret. I stedet for at beskæftige sig med både K-og y-retninger på samme tid, vil jeg bare overveje y-midten af massen.
Jeg starter med at bryde denne trekant i en flok vandrette rektangler. Her er en af disse rektangler.

så jeg kan bruge disse tynde rektangler til at finde massens centrum. Jeg skal bare multiplicere placeringen af hvert rektangel og massen af hvert rektangel. Stillingen er ret ligetil, det er “y”. Massen er lidt mere vanskelig. Bemærk også, at for rektangler, der bevæger sig op i trekanten, er de mindre med mindre masse.
området af dette lille rektangel skal være proportional med dets område. Lad mig definere arealtætheden for hele trekanten som:

det betyder, at massen af det lille rektangel vil være den lille værdi (DM), der afhænger af dets område.
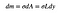
endelig skal jeg få l i form af Y. jeg vil gøre det ved først at få et udtryk i form af h. Jeg kan kalde venstre side af rektangel” h “og højre side”s”. Dette betyder, at:

men venstre side af den trekant kan beskrives som en linje med ligningen:
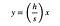
hvor (h / S) er hældningen. Jeg kan løse denne ligning for H og erstatte i udtrykket for L.

hvad med en hurtig reality check. Lad os bare sørge for, at tingene fungerer, før vi kommer for langt. Hvad hvis vi lader y = h? Det skal være øverst i trekanten med en rektangellængde på nul. JEP. Det virker. Hvad med Y = 0? Rektanglet skal have en længde på s. ser godt ud.
nu skal jeg bare sætte alle disse ting sammen. Dette er massen af den skive af et rektangel.

“s” annullerer FTV (for sejren).
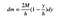
det er godt nok for nu. Det næste skridt er at skrive et udtryk for massens y-center. Da jeg vil lade bredden af dette stykke gå til nul, vil jeg få en integreret i stedet for en sum.

jeg kan integrere dette, men det er lettere, hvis jeg bryde det op i to dele. Bare en lille smule algebra giver mig:
nu Kan jeg integrere. Her er hvad jeg får.

evaluering ved grænserne (hvilket er let, da den nedre grænse er nul):

boom. Det er massens y-center. Det har endda enheder af afstand (som det skal). Bemærk også, at Y-midten af massen ikke afhænger af længden af trekanten i h-retningen (parameteren s). Det er sejt. Det betyder også, at vi nemt kan finde massens centrum. Alt jeg skal gøre er at bryde den samme trekant i lodrette rektangler.

for at gøre matematikken den samme i h-retningen, skal jeg flytte oprindelsen over til det andet hjørne af trekanten. Dette betyder, at massens centrum er (1/3) s fra højre side. Dette giver et samlet massecenter af:

cool.
numerisk beregning af Massecenter
Åh, du troede, jeg var færdig? Jeg er ikke færdig. Hvad med dette-en numerisk beregning af massecentret? Ja, det bliver sjovt. Her er min plan.
- Vælg faktiske dimensioner af en trekant. Jeg kan ikke lave en numerisk beregning med variabler. Jeg har brug for tal. Jeg har tænkt mig at bruge s = 4, h=1. Ja, der skal være enheder, men det betyder ikke noget. OK, arealtætheden er 1 (Det skal være klart, at det heller ikke betyder noget).
- vælg en lille trinstørrelse. Lad os sige, at jeg har små blokke med størrelsen 0,01 ved 0,01. Find vektorplaceringen af denne blok og dens masse (alle blokke har samme masse).
- brug sumformelversionen af massecentret.
- Flyt blokken langs, indtil alle dele af trekanten er dækket.
lad os gøre dette. OK, Der er en lille vanskelighed. Jeg bliver nødt til at lave en løkke inde i en løkke. Den ydre sløjfe bevæger disse vandrette rækker op fra 0 til h.
Her er hoveddelen af koden (fuld kode her):
while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M
med en stykkestørrelse på 0,01 ved 0,01 får jeg følgende:

Ja, jeg det er jeg ret glad for.
