hvordan kan du huske stedet på en øde ø, hvor du begravede din skat? Du vælger et vartegn, siger et palme og måler hvor mange trin nord/syd og hvor mange trin øst/vest du skal gå fra det vartegn for at komme til skatten. Det er en simpel ide, men overraskende tog matematikere århundreder at udvikle sit fulde potentiale på deres eget område. Da de endelig gjorde det, revolutionerede det matematik ved at samle to områder, der på forsiden af det har lidt at gøre med hinanden: algebra og geometri.
når vi begynder at lære geometri, tænker vi normalt på enkle former som linjer, trekanter og cirkler i det todimensionale plan. Du kan konstruere disse og mere komplicerede former ved hjælp af en lineal, kompasser og vinkelmåler. De gamle grækere var mestre ved denne type geometri: ved hjælp af bare kompasser og en lige kant (en umærket lineal) var de i stand til at konstruere en række former, og de kunne endda bevise matematiske resultater, såsom Pythagoras sætning, ved hjælp af disse enkle værktøjer.
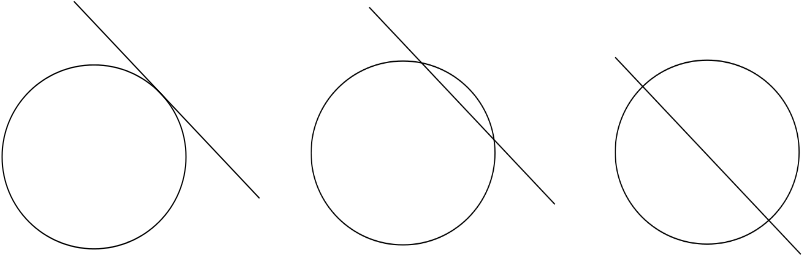
der er dog visse ting, som du ikke kan gøre ved hjælp af disse grundlæggende metoder. To former, siger en linje og en cirkel, krydser måske eller måske ikke hinanden, og de kan krydse hinanden på forskellige måder: måske rører linjen bare cirklen, måske barberer den en lille bue af den, eller måske skærer den den i to. For at registrere disse oplysninger har du brug for en måde at beskrive placeringen af figurerne på.
det er her treasure island-ideen kommer til nytte. Det illustrerer, hvad der kaldes det kartesiske koordinatsystem. Vælg et punkt i flyet, kaldet oprindelsen, og træk to vinkelrette akser gennem det, en vandret og en lodret. Ethvert punkt i Planet kan nås fra oprindelsen ved at rejse en vis afstand \(h\) langs den vandrette akse og en vis afstand \(y\) langs den lodrette akse. Tallene \((H, y)\) er koordinaterne for punktet. Oprindelsen selv har koordinater \((0,0)\). Den del af den vandrette akse(også kaldet \(H\)-aksen), der ligger til venstre for oprindelsen og den del af den lodrette akse (\(y\)-aksen) under oprindelsen er beskrevet med negative tal.
kartesiske koordinater er opkaldt efter det 17.århundrede franske filosof og matematiker ren Kristian Descartes. Der er en (sandsynligvis usand) historie om, at Descartes opfandt disse koordinater, mens han lå i sengen og så på en flue i loftet og spekulerede på, hvordan man beskriver dens placering. Descartes ‘ forkærlighed for at ligge i sengen indtil middag kan faktisk have været årsagen til hans død, der fandt sted i Stockholm i 1650. Descartes var i Sverige for at fungere som matematiklærer for dronning Christina, som Desværre foretrak at arbejde tidligt om morgenen. Ifølge nogle rapporter var det disse tidlige timer og de skandinaviske temperaturer, der forårsagede lungebetændelsen, der til sidst dræbte ham. Andre har antydet, at han blev forgiftet af en katolsk præst, der var bekymret for Descartes’ radikale teologi.
uanset hvad er det kartesiske koordinatsystem en af Descartes’ vigtigste arv (selvom han ikke var den eneste person, der havde ideen). Det giver os mulighed for at besvare geometriske problemer ved hjælp af algebra og visualisere algebraiske forhold, der ellers ville forblive ret abstrakte. Tag for eksempel ligningen \ vi kan plotte grafen for denne funktion i et kartesisk koordinatsystem ved at plotte alle punkter, hvis koordinater er af formen \((2H-1)\): punkter som \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), og \((1.73, 2.46)\). I dette tilfælde er grafen en lige linje,der opfylder \(y\)-aksen ved punktet \((0, -1)\) og har en hældning på \(2\).
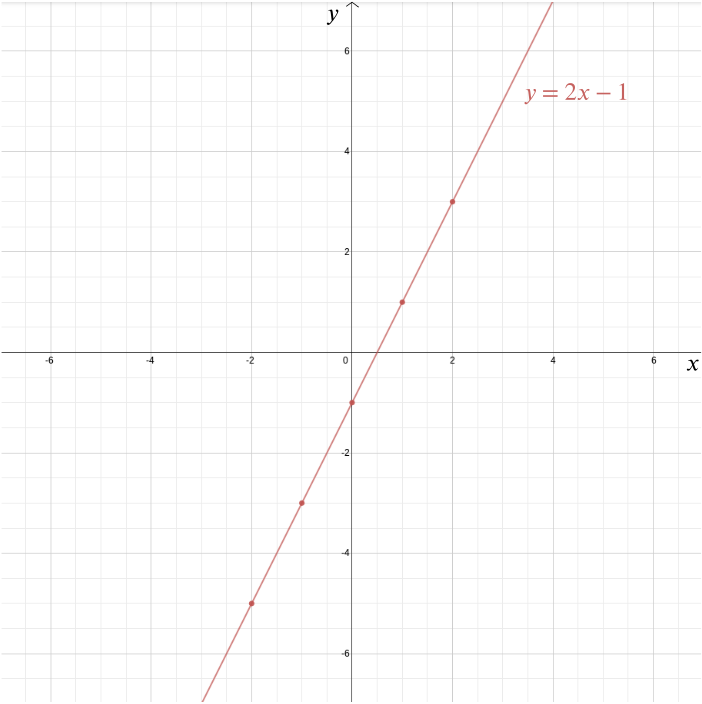
mere generelt er hver lige linje givet ved en ligning af formularen \ hvor \(m\) giver dig linjens hældning og \((0,b)\) er det punkt, hvor det krydser \(y\)-aksen. En lodret linje, der ikke krydser \(y\)-aksen, er givet ved en ligning af formularen \(C=c\). I dette tilfælde er \((c, 0)\) det punkt, hvor det krydser \(h\)-aksen.
hvad med en cirkel? En cirkel består af alle de punkter, der ligger på lige afstand \(r\) fra et givet punkt \(m\). Lad os antage, at \(m\) er punktet \((0,0)\). Fra Pythagoras sætning ved vi, at hvis et punkt \((H, y)\) ligger i afstand \(r\) fra \((0,0)\), så \
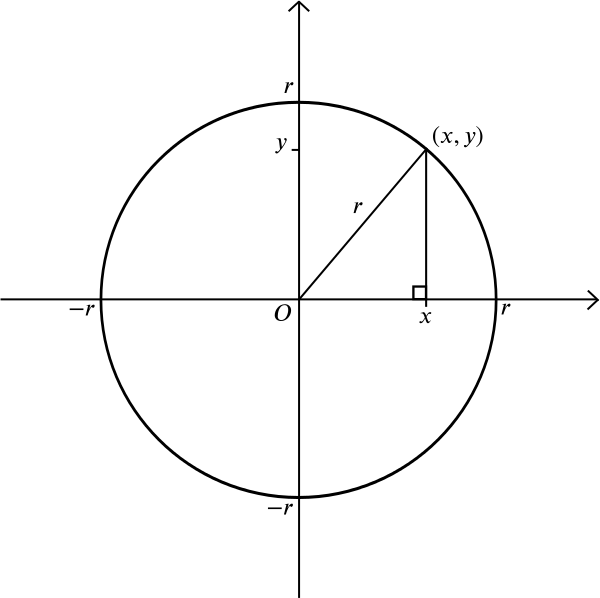
Dette er derfor ligningen af en cirkel med radius \(r\) centreret om oprindelsen. Du kan selv finde ud af, at en cirkel med radius \(r\) centreret om punktet \((a, b)\) har ligningen \ men her er et mere kompliceret spørgsmål: hvilken form får du, når du overvejer alle punkter, der ligger lige langt fra et givet punkt og en given linje? Uden et koordinatsystem kan du tegne punktet og linjen og eksperimentere med din lineal eller kompasser. Du kan tegne et par punkter, der ligger i lige stor afstand fra begge og se om du kan gætte den overordnede form.
bevæbnet med et koordinatsystem bliver svaret meget lettere og meget mere præcist. Antag at det givne punkt er i afstand \(1\) fra den givne linje. Lad os placere det givne punkt ved oprindelsen og den givne linje, så den er vandret,givet ved ligningen \ ved Pythagoras sætning afstanden til ethvert punkt \((H, y)\) fra \((0,0)\) er \(\kvm{H^2 + y^2}\). Afstanden fra et punkt \(Y, y)\) til linjen \(y = -1\) er \(|y+1|\) (Vi bruger den absolutte værdi her, fordi \(y\)-koordinaten kan være negativ). Hvis disse to er ens, giver \ kvadrering af begge sider \ omarrangering giver \ så ethvert punkt i lige afstand fra punktet \((0,0)\) og linjen \(y=-1\) har koordinater \(\venstre(h, \frac{H^2}{2} – \frac{1}{2}\højre)\). Du kan selv kontrollere, at det omvendte også er sandt: hvert punkt med disse koordinater ligger i lige afstand fra punktet \((0,0)\) og linjen \(y=-1\).
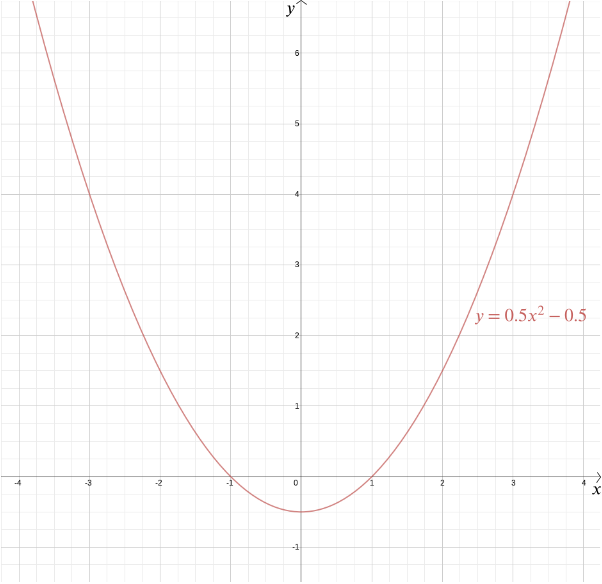
Vi kan plotte grafen for denne funktion for at se den ønskede form, som viser sig at være en parabola. Faktisk giver hver kvadratisk funktion \ for \(a\), \(b\) og \(c\) konstanter os en parabel. Denne velkendte form, som kan komme i så mange subtile variationer—lang og tynd eller knebøj og flad—er fanget af dette praktiske algebraiske udtryk. Det faktum, at udtrykkene “kvadratisk funktion” og “parabola” i dag næsten betragtes som synonyme, fremhæver, hvor vellykket Descartes’ ide har været. Mere generelt giver ethvert algebraisk forhold mellem to variabler \(Y\) og \(y\) os en kurve, som vi kan plotte ved hjælp af kartesiske koordinater.
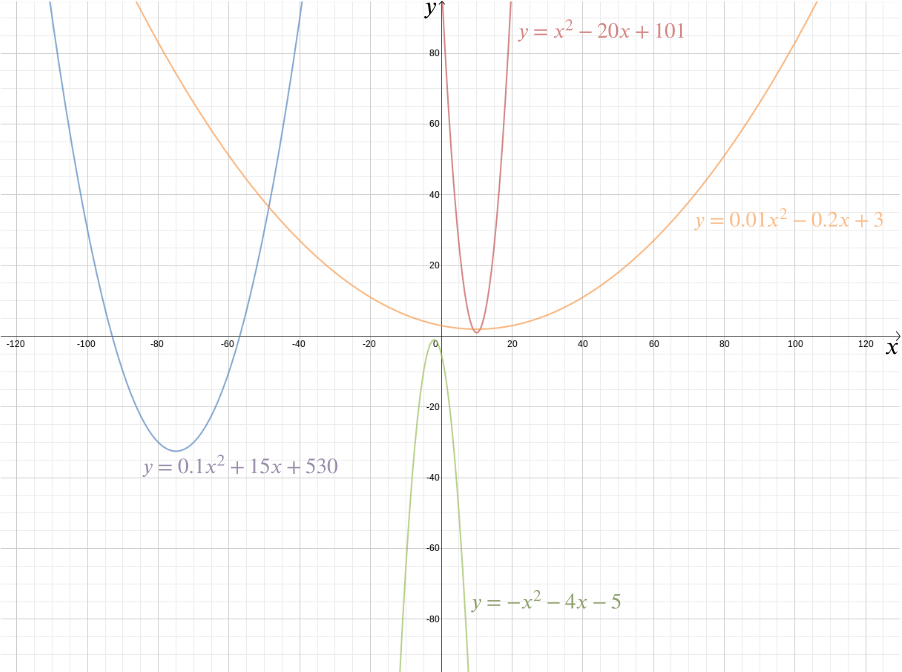
den algebraiske repræsentation gør det nemt at besvare en lang række geometriske spørgsmål. For at finde ud af skæringspunkterne for linjen givet af \ og parabolen \(y = \frac{H^2}{2} – \frac{1}{2}\) bemærker vi simpelthen, at \(y\) koordinaten for ethvert punkt \((H,y)\) liggende på begge skal tilfredsstille begge ligninger, så \ dette giver \ løsning af den kvadratiske ligning, vi får \ og \ så skæringspunkterne er ved \
bortset fra at løse geometriske problemer hjælper kartesiske koordinater også med at visualisere algebraiske forhold. Antag for eksempel, at en bil kører med hastighed \(u\), og føreren anvender bremserne, hvilket resulterer i en konstant deceleration på for eksempel \(-4\) meter/sekunder\(^2\). Stopafstanden \(s\)—den afstand, bilen dækker, før den stopper-er givet af det algebraiske forhold \ plotte dette ved hjælp af kartesiske koordinater bringer hjem, hvor vigtigt det er at bremse i byområder, fordi stopafstanden stiger hurtigt med \(u\).
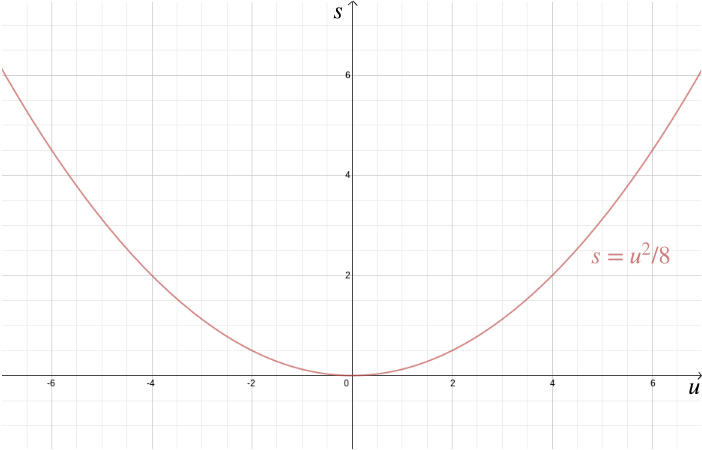
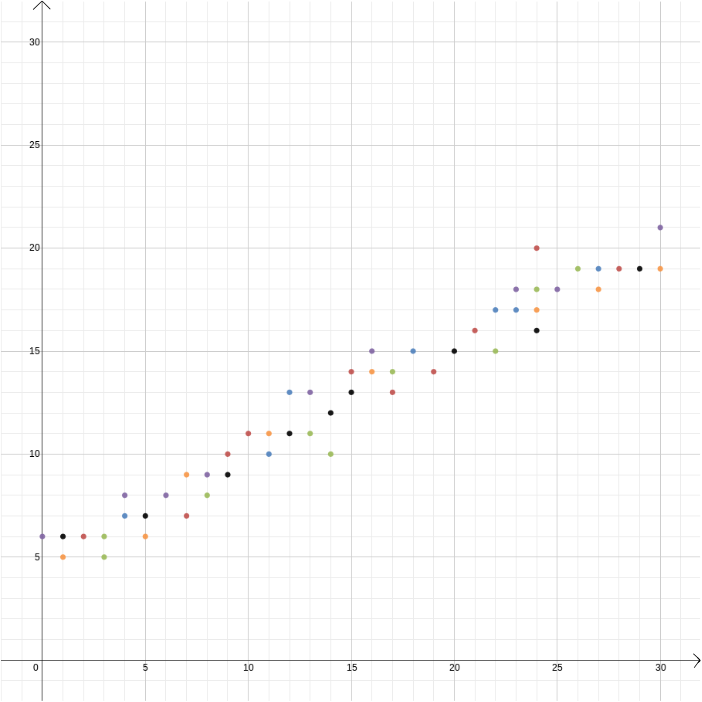
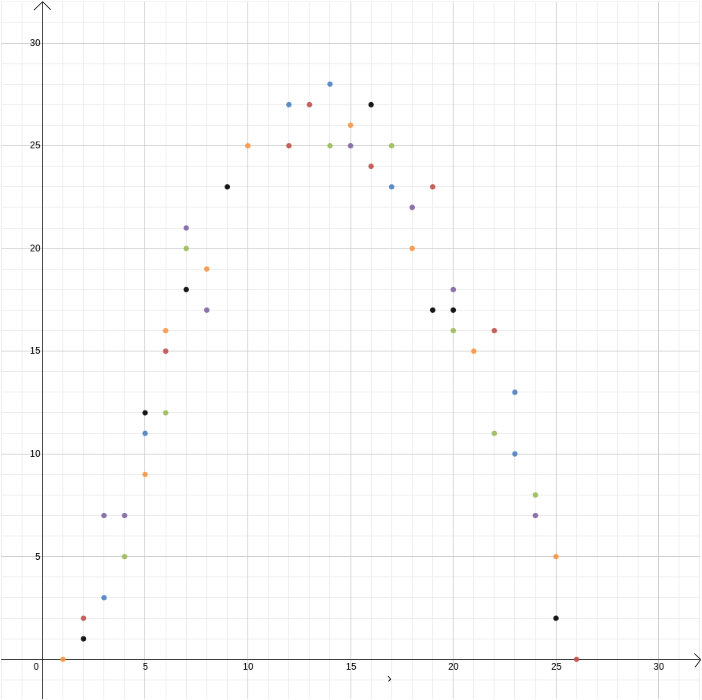
i dette eksempel vidste vi forholdet mellem to variabler, fordi det kan udledes af fysikkens love. Men kartesiske koordinater er også nyttige, når du har mistanke om, at to variabler er relaterede, men du ved ikke hvordan. Antag, at vi tror, at der er et forhold mellem fortjenesten fra en is sælger og udetemperaturen. For at finde ud af, hvad dette forhold kan være, kan vi måle temperatur og fortjeneste over et års forløb og plotte værdierne mod hinanden med temperatur registreret på \(h\)-aksen og fortjeneste på \(y\)-aksen. Vi kan så se, om vi kan få øje på et mønster. I det første diagram nedenfor kan vi gætte, at forholdet er lineært, og vi kan forsøge at finde den lige linje\, der passer bedst til vores data (der er metoder til at finde den bedste pasform). I det andet diagram nedenfor kan vi gætte, at forholdet er kvadratisk, og igen kan vi prøve at finde den funktion\, der bedst passer til dataene.
kartesiske koordinater spillede en vigtig rolle i udviklingen af calculus i anden halvdel af det 17.århundrede. Calculus gør det muligt at udarbejde attributter af kurver som deres hældning på et givet punkt eller det område af regionen, der ligger mellem en kurve og aksen. Disse kan også have fysiske fortolkninger. For eksempel, hvis vi planlægger den afstand, en bil kører mod den tid, den har kørt, repræsenterer hældningen af den resulterende kurve på et givet tidspunkt—hastigheden for ændring af afstand med hensyn til tid—den hastighed, hvormed bilen kørte på det tidspunkt: det er afledt af funktionen, der giver os afstand med hensyn til tid. Se også Hvorfor er gradienter vigtige i den virkelige verden?.
Vi kan også gå op i en dimension ved at overveje en tredje akse vinkelret på de to første, som du kan forestille dig at komme ud af dit ark papir og pege på dig. Ved hjælp af et sådant tredimensionelt system kan du nu repræsentere tredimensionelle objekter og visualisere, hvordan en tredje variabel \(å\) afhænger af dine første to, \(H\) og \(y\).
disse eksempler skal give dig en fornemmelse af, hvorfor koordinater er blevet så uundværlige inden for alle videnskabsområder, fra fysik til astronomi og teknik, og også i visuelle industrier til at producere computergrafik og det computergenererede billedsprog, vi beundrer i film og spil.
i selve matematikken har forbindelsen mellem algebra og geometri kulmineret i et helt område kaldet algebraisk geometri, som har en egen fascination. Måske er det mest berømte resultat, der er opstået fra dette område, Fermats sidste sætning, opkaldt efter en samtid af Descartes, Pierre de Fermat, som også bidrog væsentligt til udviklingen af det kartesiske koordinatsystem. Fermat overvejede et spørgsmål, der forbinder geometri til talteori. Ifølge Pythagoras sætning, Hvis \(A\), \(b\) og \(c\) er siderne af en retvinklet trekant og \(c\) er siden modsat den rigtige vinkel, så \(a^2 + b^2 = c^2\). Der er uendeligt mange tredobler af hele tal \(A\), \(b\) og \(c\), som tilfredsstiller dette forhold; \((3,4,5)\) er et eksempel.
Antag nu, at vi ændrer eksponenten og overvejer udtryk som \ og \ og mere generelt \ hvor \(n\) er et naturligt tal større end \(2\). Kan vi stadig finde positive hele tal \(A\), \(b\) og \(c\), der opfylder ligningen? Fermat mistanke om, at vi ikke kan, og han scribbled så meget i margenen af hans matematik tekstbog, siger han havde en “fantastisk bevis” for det faktum, som margenen var for snæver til at indeholde.
at scribble var at hjemsøge matematikere i over 350 år. Det var først i 1994, at et korrekt bevis på dette tilsyneladende uskadelige resultat endelig blev annonceret af matematikeren Andrei viles. Viljer havde gjort omfattende brug af algebraisk geometri. Især havde han brugt resultater vedrørende de elliptiske kurver beskrevet af punkter i flyet, hvis koordinater tilfredsstiller Descartes’ overvejelse af en flue er kommet langt!
