En trin-for-trin guide til opbygning af en simpel skak AI

af Lauri Hartikka

lad os udforske nogle grundlæggende begreber, der vil hjælpe os med at skabe en simpel skak AI:

Flyt generation
board evaluering
Minimaks
og alpha beta beskæring.

på hvert trin forbedrer vi vores algoritme med en af disse tidstestede skakprogrammeringsteknikker. Jeg vil demonstrere, hvordan hver påvirker algoritmens spillestil.

Du kan se den endelige AI-algoritme her på GitHub.

Trin 1: Flyt generation og board visualisering

Vi bruger skak.JS bibliotek til flytte generation, og skakbræt.js til visualisering af bestyrelsen. Move generation-biblioteket implementerer dybest set alle reglerne for skak. Baseret på dette kan vi beregne alle lovlige træk for en given bestyrelsesstat.

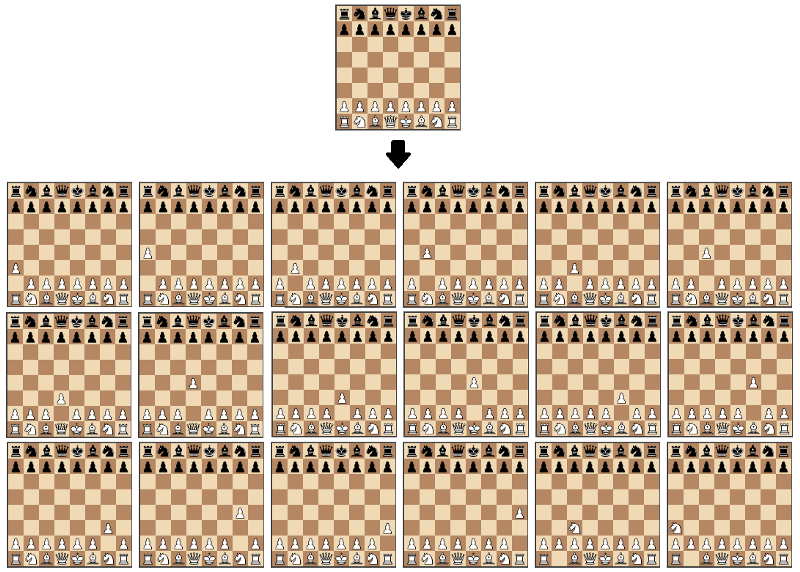
en visualisering af move generation-funktionen. Startpositionen bruges som input, og output er alle mulige bevægelser fra den position.

brug af disse biblioteker hjælper os kun med at fokusere på den mest interessante opgave: oprettelse af den algoritme, der finder det bedste træk.

Vi starter med at oprette en funktion, der bare returnerer et tilfældigt træk fra alle de mulige træk:

selvom denne algoritme ikke er en meget solid skakspiller, er det et godt udgangspunkt, da vi faktisk kan spille imod det:

Sort spiller tilfældige træk. Kan afspilles på https://jsfiddle.net/lhartikk/m14epfwb/4

Trin 2 : Position evaluering

lad os nu prøve at forstå, hvilken side der er stærkere i en bestemt position. Den enkleste måde at opnå dette på er at tælle den relative styrke af stykkerne på tavlen ved hjælp af følgende tabel:

med evalueringsfunktionen er vi i stand til at oprette en algoritme, der vælger det træk, der giver den højeste evaluering:

den eneste håndgribelige forbedring er, at vores algoritme nu vil fange et stykke, hvis det kan.

Sort spiller ved hjælp af den enkle evalueringsfunktion. Kan afspilles på https://jsfiddle.net/lhartikk/m5q6fgtb/1/

Trin 3: Søg træ ved hjælp af Minimaks

næste skal vi oprette et søgetræ, hvorfra algoritmen kan vælge det bedste træk. Dette gøres ved hjælp af Minimaksalgoritmen.

i denne algoritme udforskes det rekursive træ af alle mulige bevægelser til en given dybde, og positionen evalueres ved slutningen “blade” af træet.

derefter returnerer vi enten den mindste eller den største værdi af barnet til forældreknudepunktet, afhængigt af om det er en hvid eller sort at flytte. (Det vil sige, vi forsøger enten at minimere eller maksimere resultatet på hvert niveau.)

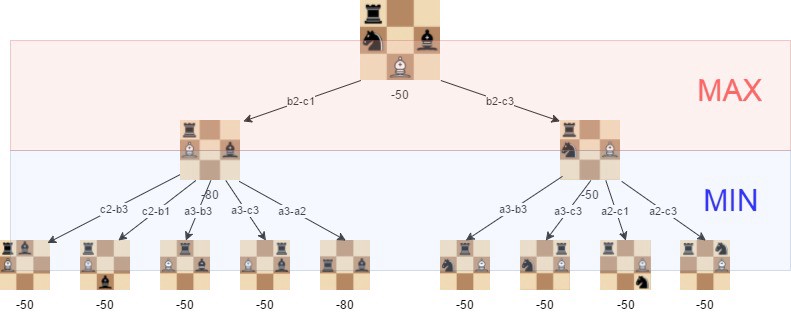
en visualisering af minimaksalgoritmen i en kunstig position. Det bedste træk for hvid er b2-c3, fordi vi kan garantere, at vi kan komme til en position, hvor evalueringen er -50

med minimaks på plads begynder vores algoritme at forstå nogle grundlæggende taktikker for skak:

Minimaks med dybdeniveau 2. Kan afspilles på: https://jsfiddle.net/k96eoq0q/1/

effektiviteten af minimaksalgoritmen er stærkt baseret på den søgedybde, vi kan opnå. Dette er noget, vi forbedrer i det følgende trin.

Trin 4: Alpha-beta beskæring

Alpha-beta beskæring er en optimeringsmetode til minimaksalgoritmen, der giver os mulighed for at se bort fra nogle grene i søgetræet. Dette hjælper os med at evaluere søgetræet meget dybere, mens du bruger de samme ressourcer.alfa-beta beskæringen er baseret på den situation, hvor vi kan stoppe med at evaluere en del af søgetræet, hvis vi finder et træk, der fører til en værre situation end et tidligere opdaget træk.

alfa-beta — beskæringen påvirker ikke resultatet af minimaks-algoritmen-det gør det kun hurtigere.alfa-beta-algoritmen er også mere effektiv, hvis vi tilfældigvis først besøger de stier, der fører til gode træk.

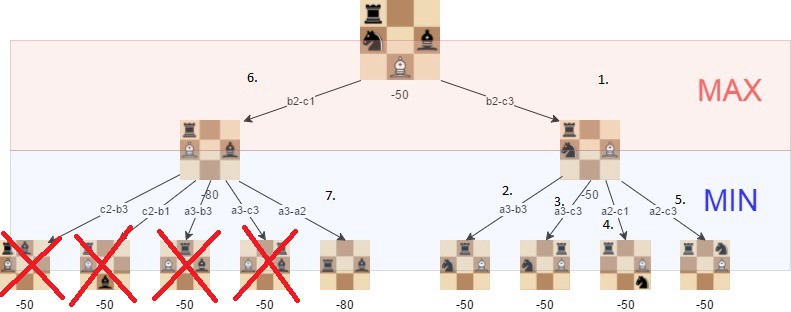
de positioner, vi ikke behøver at undersøge, om alfa-beta beskæring erbrugt, og træet besøges i den beskrevne rækkefølge.

med alpha-beta får vi et betydeligt løft til minimaksalgoritmen, som vist i følgende eksempel:

antallet af positioner, der kræves for at evaluere, om vi vil udføre en søgning med dybde på 4, og” root ” – positionen er den, der vises.

Følg dette link for at prøve alpha-beta forbedret version af skak AI.

Trin 5: forbedret evalueringsfunktion

den indledende evalueringsfunktion er ret naiv, da vi kun tæller det materiale, der findes på tavlen. For at forbedre dette tilføjer vi evalueringen en faktor, der tager højde for stykkernes position. For eksempel er en ridder i midten af brættet bedre (fordi den har flere muligheder og dermed er mere aktiv) end en ridder på kanten af brættet.

Vi bruger en let justeret version af brik-firkantede tabeller, der oprindeligt er beskrevet i skakprogrammeringen.

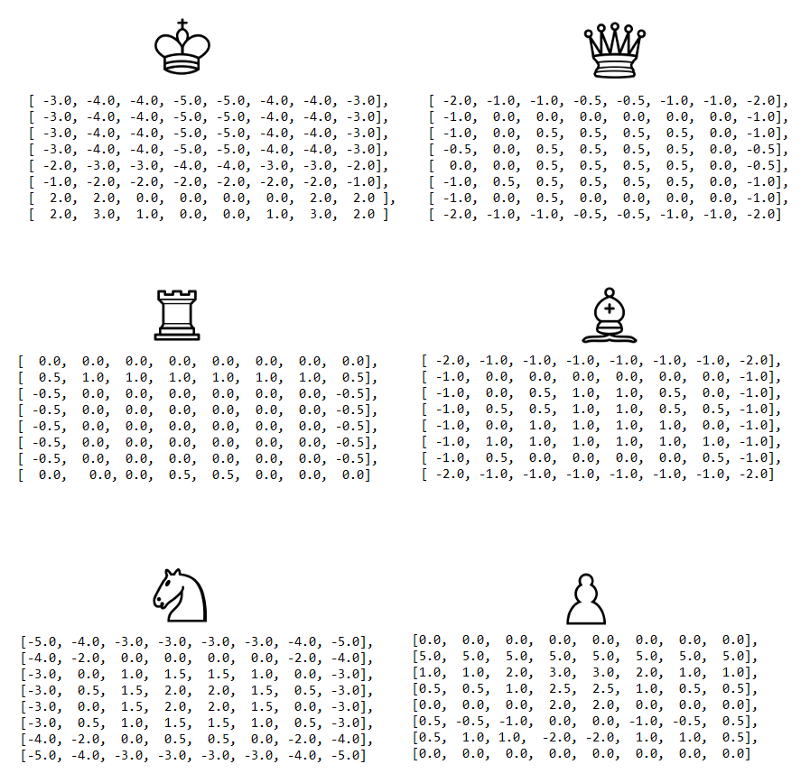
det visualiserede stykke-firkantede tabeller visualiseret. Vi kan reducere eller øge evalueringen afhængigt af placeringen af stykket.

med følgende forbedring begynder vi at få en algoritme, der spiller noget “anstændigt” skak, i det mindste set fra en afslappet spiller:

forbedret evaluering og alfa-beta beskæring med søgedybde på 3. Afspilles på https://jsfiddle.net/q76uzxwe/1/

konklusioner

styrken af selv en simpel skakspilalgoritme er, at den ikke laver dumme fejl. Når det er sagt, mangler det stadig strategisk forståelse.

med de metoder, jeg introducerede her, har vi været i stand til at programmere en skak-spiller-algoritme, der kan spille grundlæggende skak. Den” AI-del ” (Flyt-generation udelukket) af den endelige algoritme er kun 200 linjer kode, hvilket betyder, at de grundlæggende begreber er ret enkle at implementere. Du kan tjekke den endelige version er på GitHub.

nogle yderligere forbedringer, vi kunne foretage i algoritmen, ville være for eksempel:

Flyt-bestilling
hurtigere Flyt generation
og slutspilsspecifik evaluering.

KGSAU