der er mere end en måde at opsummere en uendelig serie på. Ces larro summation giver dig mulighed for at beregne summen af serier, der ikke har en sum i klassisk forstand.
Antag, at vi har en uendelig serie
den nte delvise sum af serien er givet af
den klassiske sum af serien, hvis den findes, er defineret til at være grænsen for dens delvise summer. Det vil sige
ces Larro summation tager en anden tilgang. I stedet for at tage grænsen for delbeløb, tager den grænsen for gennemsnittet af delbeløb. For at være specifik, Definer
og definer ces Pristro summationen for at være grænsen for Cn, da n går til uendelig. Hvis en serie har en sum i klassisk forstand, har den også en sum i CES Larro-forstand, og grænserne er de samme. Men nogle serier har en ces Larro sum, der ikke har en klassisk sum. Eller måske findes begge grænser, men mellemtrinnene i CES Larro summation er bedre opført, som vi vil se i et eksempel nedenfor.
Hvis du udtrykker Cn i form af de originale an-udtryk, får du
med andre ord er den nte ces-delvise sum en genvejning af de klassiske delvise Summer, hvor vægtene ændres som en funktion af n. Bemærk, at for fast i, fraktionen multiplicerer ai går til 1 som n stiger.
fej larr summation og Gibbs fænomen
fej larr summation er ces Larro summation anvendt på Fourier-serien. De (almindelige) delvise summer af en Fourier-serie giver den bedste tilnærmelse til en funktion målt ved mindst kvadrater norm. Men ces Kroro delbeløb kan være kvalitativt mere som den funktion, der tilnærmes. Vi demonstrerer dette nedenfor med en firkantet bølge.
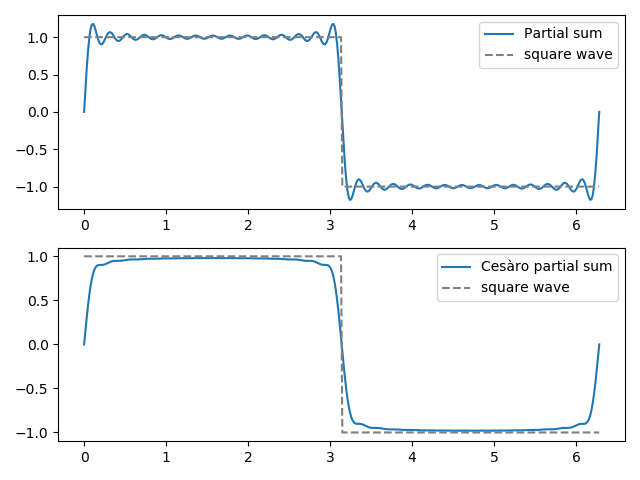
den 30.almindelige delvise sum viser begyndelsen på Gibbs-fænomenet, “flagermusørene” øverst på firkantbølgen og deres spejlbillede i bunden. Den 30. delvise ces-sum er glattere og eliminerer Gibbs-fænomener nær diskontinuiteten i firkantbølgen.
flere Fourier series indlæg
- Fourier-Bessel series
- modeksempel til Dirichlet princip
- klippede sinusbølger
