teď Pojďme na tento. Odvozím výraz pro těžiště pravoúhlého trojúhelníku. Proč?

Uvidíte, budeme se bavit. Už jsem zahrnul Yoda mem. Co by se mohlo pokazit?

zde je trojúhelník.

Oh, to vypadá jako normální modrý trojúhelník. Že? Předpokládejme však, že se jedná o nějaký tenký plech s hmotností m. jak byste našli umístění středu hmoty? Začněme základní definicí těžiště.

Toto je v podstatě vážený průměr. OK, je to vážený průměr. Pokud však objekt rozbijete na spoustu malých kusů, vynásobte vektorovou polohu každé hmoty a její malou hmotnost. Pak přidáte vše a vydělíte celkovou hmotností. To je těžiště hmoty. Tady je další obrázek.

Samozřejmě v tomto případě nemáme na kousky. Máme spojitou hmotu. To znamená, že můžeme místo toho přeměnit součet na integrál. Místo toho, abych se zabýval oběma směry x a y současně, budu zvažovat y – střed hmoty.

začnu tím, že tento trojúhelník rozbiju na spoustu vodorovných obdélníků. Tady je jeden z těch obdélníků.

Můžu použít tyhle úzké obdélníky najít těžiště. Jen musím znásobit polohu každého obdélníku a hmotnost každého obdélníku. Pozice je docela přímočará, je to „y“. Hmota je trochu složitější. Všimněte si také, že u obdélníků, které se pohybují nahoru po trojúhelníku, jsou menší s menší hmotností.

plocha tohoto malého obdélníku by měla být úměrná jeho ploše. Dovolte mi definovat oblast, hustota pro celou trojúhelník jako:

to znamená, Že hmotnost malého obdélníku bude malé hodnoty (dm) to závisí na jeho oblasti.

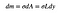
a Konečně, musím se dostat L, pokud jde o y. Budu dělat, že tím, že nejprve získat vyjádření z hlediska x. Mohu nazvat levou stranu obdélníku “ x „a pravou stranu „s“. To znamená, že:

Ale na levou stranu, že trojúhelník může být popsán jako přímka s rovnicí:

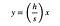
Where (h/s) je na svahu. Mohu vyřešit tuto rovnici pro x a nahradit výrazem pro L.

Jak se o kontrolu rychlý skutečnost. Jen se ujistíme, že věci fungují, než se dostaneme příliš daleko. Co když necháme y = h? To by mělo být v horní části trojúhelníku s délkou obdélníku nula. Jo. Práce. A co y = 0? Obdélník by měl mít délku s. vypadá dobře.

teď musím dát všechny tyto věci dohromady. Toto je hmotnost tohoto řezu obdélníku.

„s“ zruší FTW (for the win).

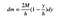
to je dost dobré pro teď. Dalším krokem je napsat výraz pro y – střed hmoty. Vzhledem k tomu, že nechám šířku tohoto kusu jít na nulu, dostanu integrál místo součtu.

lze integrovat to, ale je to jednodušší, když jsem rozbít to do dvou částí. Jen trochu z algebry, mi dává:

Teď můžu integrovat. Tady je to, co jsem si.

Vyhodnocení na limity (což je snadné, protože spodní hranice je nulová):

Boom. To je y – střed hmoty. Má dokonce jednotky vzdálenosti(které by měly). Všimněte si také, že y-střed hmotnosti nezávisí na délce trojúhelníku ve směru x (parametr s). To je v pohodě. To také znamená, že můžeme snadno najít x-centrum hmoty. Vše, co musím udělat, je rozdělit ten stejný trojúhelník na svislé obdélníky.

Aby matematiky stejné ve směru x, já bych třeba přesunout počátek průběhu do druhého rohu trojúhelníku. To znamená, že x-střed hmotnosti je (1/3) s z pravé strany. To dává celkem těžiště:

v Pohodě.

numerický výpočet těžiště

Oh, mysleli jste, že jsem skončil? Ještě jsem neskončil. Co takhle-numerický výpočet těžiště? Ano, bude to zábava. Tady je můj plán.

• Vyberte skutečné rozměry trojúhelníku. Neumím numerický výpočet s proměnnými. Potřebuju čísla. Použiji s = 4, h=1. Ano, měly by tam být jednotky, ale na tom nezáleží. OK, hustota plochy je 1 (mělo by být jasné, že na tom také nezáleží).
• vyberte malou velikost kroku. Řekněme, že mám malé bloky o velikosti 0,01 x 0,01. Najděte vektorové umístění tohoto bloku a jeho hmotnost (všechny bloky mají stejnou hmotnost).
• použijte součet vzorec verze těžiště.
• pohybujte blokem, dokud nejsou pokryty všechny části trojúhelníku.

Udělejme to. OK, Tam je malý problém. Budu muset udělat smyčku uvnitř smyčky. Vnitřní smyčka bude přidávat až čtverců podél x-osy od levého svahu k x = h. Vnější smyčka bude přesun těchto vodorovných řadách od 0 do h.

Tady je hlavní část kódu (úplný kód):

while y<=h:
x=(s/h)*y
while x<=s:
r=vector(x,y,0) rsum=dm*r+rsum
x=x+dx
y=y+dyA=.5*s*h
M=sigma*Arcm=rsum/M

S kusem velikosti 0.01 do 0.01, jsem si následující:

Jo, jsem docela spokojený s tím.