Jak vzpomínáte na místě na pustém ostrově, kde si zakopal svůj poklad? Vyberete orientační bod, řekněme palmu a změříte, kolik kroků na sever / jih a kolik kroků na východ / západ musíte jít od tohoto orientačního bodu, abyste se dostali k pokladu. Je to jednoduchý nápad, ale překvapivě, matematici trvalo staletí rozvíjet svůj plný potenciál ve svém oboru. Když to konečně udělali, revolucionizovalo matematiku spojením dvou oblastí, které na první pohled nemají nic společného: algebra a geometrie.
Když se začneme učit geometrii, obvykle myslíme na jednoduché tvary, jako jsou čáry, trojúhelníky a kruhy ve dvourozměrné rovině. Tyto a složitější tvary můžete postavit pomocí pravítka, kompasů a úhloměru. Starověcí Řekové byli mistři tohoto typu geometrie: pomocí kružítka a pravítka (neoznačený pravítko) byli schopni vytvořit řadu tvarů a dokonce můžou dokázat matematické výsledky, jako Pythagoras teorém, pomocí těchto jednoduchých nástrojů.
existují však určité věci, které nelze provést pomocí těchto základních metod. Dva tvary, říci čáry a kruhu, může nebo nemusí protínat, a oni mohou protínat v různých způsobech: možná, že linka jen dotkne kruhu, možná to holení trochu oblouk, nebo možná to snižuje na polovinu. Chcete-li zaznamenat tyto informace, potřebujete způsob popisu umístění tvarů.
zde je myšlenka ostrova pokladů užitečná. Ilustruje to, co se nazývá Kartézský souřadnicový systém. Vyberte bod v rovině, nazvaný původ, a nakreslete dvě kolmé osy, jednu vodorovnou a jednu svislou. Jakýkoli bod v rovině lze dosáhnout Od počátku ujetím určité vzdálenosti \(x\) podél vodorovné osy a určité vzdálenosti \(y\) podél svislé osy. Čísla \((x, y)\) jsou souřadnice bodu. Samotný počátek má souřadnice \((0,0)\). Část vodorovné osy (nazývaná také osa \(x\)), která leží vlevo od počátku, a část svislé osy(osa \(y\)) pod počátkem jsou popsány zápornými čísly.
kartézské souřadnice jsou pojmenovány podle francouzského filozofa a matematika 17. století Reného Descartese. Existuje (pravděpodobně nepravdivý) příběh, který Descartes vynalezl tyto souřadnice, zatímco ležel v posteli a sledoval mouchu na stropě a přemýšlel, jak popsat její polohu. Descartesova záliba ležet v posteli až do poledne mohla být ve skutečnosti příčinou jeho zániku, ke kterému došlo ve Stockholmu v roce 1650. Descartes byl ve Švédsku, aby působil jako učitel matematiky královny Christiny, která bohužel raději pracovala brzy ráno. Podle některých zpráv to byly tyto časné hodiny a skandinávské teploty, které způsobily zápal plic, který ho nakonec zabil. Jiní navrhli, že byl otráven katolickým knězem, který se obával Descartesovy radikální teologie.
ať tak či onak, Kartézský souřadný systém je jedním z Descartes‘ nejvíce důležité odkazy (i když nebyl jediný, kdo měl nápad). Umožňuje nám odpovědět na geometrické problémy pomocí algebry a vizualizovat algebraické vztahy, které by jinak zůstaly docela abstraktní. Vezměte si například rovnici \ můžeme vykreslit graf této funkce v Kartézském souřadném systému vynesením všech bodů, jejichž souřadnice jsou ve tvaru \((x,2x-1)\): body jako \((0, -1)\), \((1, 1)\), \((2,3)\), \((-1,-3)\), \((-2,-5)\), \((-\frac{1}{2}, -2)\), a \((1.73, 2.46)\). V tomto případě je graf přímkou, která splňuje osu \(y\) v bodě \((0, -1)\) a má sklon \(2\).
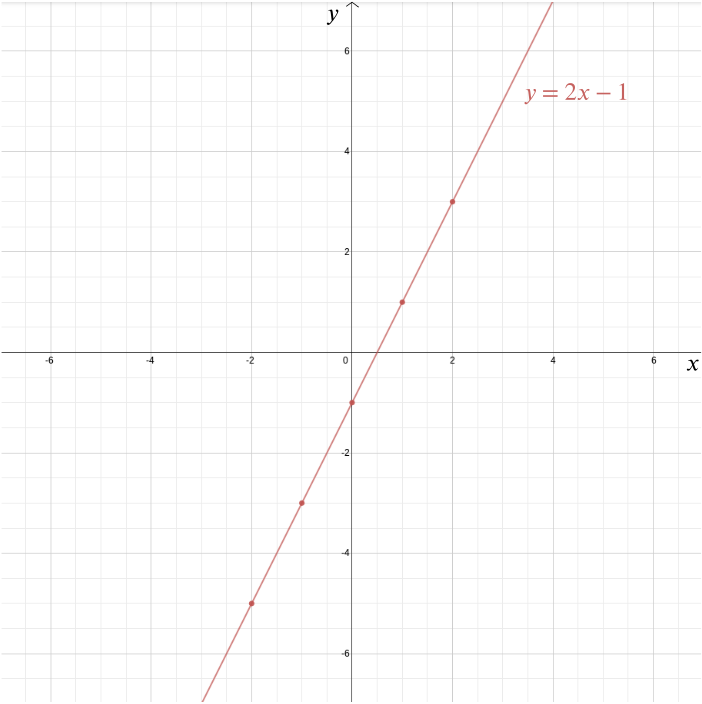
Více obecně každá přímka je dána rovnicí ve tvaru \ kde \(m\) vám dává sklon přímky a \((0,b)\), je bod, ve kterém se kříží \(y\)-osa. Svislá čára, která nepřekročí osu \(y\), je dána rovnicí tvaru \(x=c\). V tomto případě \((c, 0)\) je bod, ve kterém protíná osu \(x\).
a co kruh? Kruh se skládá ze všech bodů, které leží ve stejné vzdálenosti \(r\) od daného bodu \(m\). Předpokládejme, že \(m\) je bod \((0,0)\). Z Pythagoras teorém víme, že pokud bod \((x, y)\) leží ve vzdálenosti \(r\) od \((0,0)\), pak \
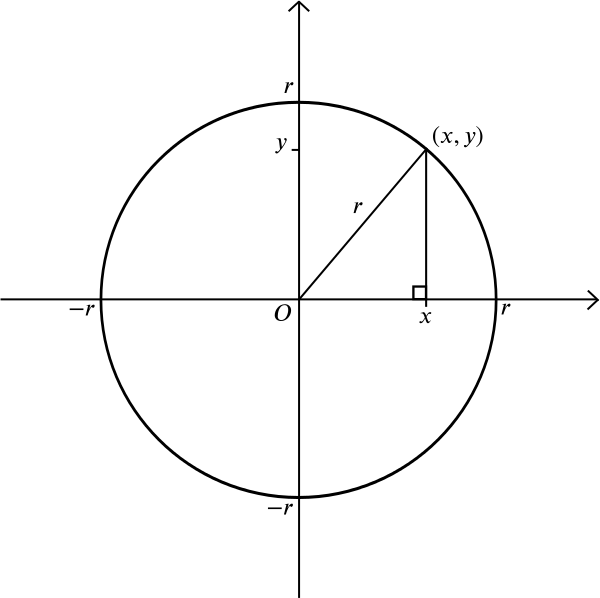
Jedná se tedy o rovnici kružnice o poloměru \(r\) soustředěnou na počátek. Můžete si sami zjistit, že kružnice o poloměru \(r\) soustředěná na bod \((a, b)\) má rovnici \ , ale zde je složitější otázka: jaký tvar získáte, když vezmete v úvahu všechny body, které leží ve stejné vzdálenosti od daného bodu a dané čáry? Bez souřadnicového systému můžete nakreslit bod a čáru a experimentovat s pravítkem nebo kompasy. Můžete nakreslit několik bodů, které leží ve stejné vzdálenosti od obou, a zjistit, zda můžete odhadnout celkový tvar.
vyzbrojen souřadnicovým systémem, ačkoli, odpověď se stává mnohem jednodušší a mnohem přesnější. Předpokládejme, že daný bod je ve vzdálenosti \(1\) od daného řádku. Pojďme umístit daný bod na počátku a na dané trati tak, že je horizontální, je dána rovnicí \ Tím, Pythagoras teorém vzdálenost libovolného bodu \((x,y)\) z \((0,0)\) je \(\sqrt{x^2 + y^2}\). Vzdálenost od bodu \((x, y)\) k přímce \(y = -1\) je \(/y+1/\) (zde používáme absolutní hodnotu, protože souřadnice \(y\) může být záporná). Pokud tyhle dvě jsou si rovny, pak \ Kvadratura obou stranách dává \ Uspořádání dává \ Takže jakýkoli bod, ve stejné vzdálenosti od bodu \((0,0)\) a přímka \(y ‚ =-1\) má souřadnice \(\left(x, \frac{x^2}{2} – \frac{1}{2}\right)\). Můžete si sami ověřit, že konverzace je také pravdivá: každý bod s těmito souřadnicemi leží ve stejné vzdálenosti od bodu \((0,0)\) a čáry \(y=-1\).
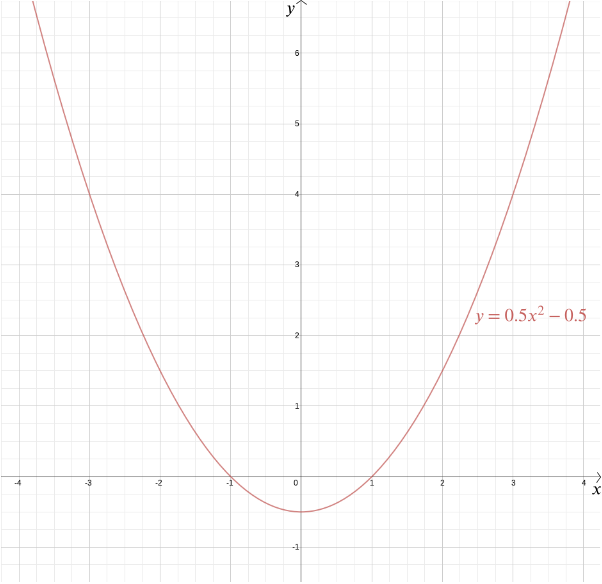
můžeme vykreslit graf této funkce viz požadovaného tvaru, který se ukáže být parabola. Ve skutečnosti každá kvadratická funkce \ pro \(A\), \(b\) A \(c\) konstanty nám dává parabolu. Tento známý tvar, který může přijít v tolika jemných variacích-dlouhý a tenký nebo squat a plochý-je zachycen tímto praktickým algebraickým výrazem. Skutečnost, že dnes jsou pojmy „kvadratická funkce“ a „parabola“ téměř považovány za synonymum, zdůrazňuje, jak úspěšný byl Descartesův nápad. Obecněji, jakýkoli algebraický vztah mezi dvěma proměnnými \(x\) a \(y\) nám dává křivku, kterou můžeme vykreslit pomocí kartézských souřadnic.
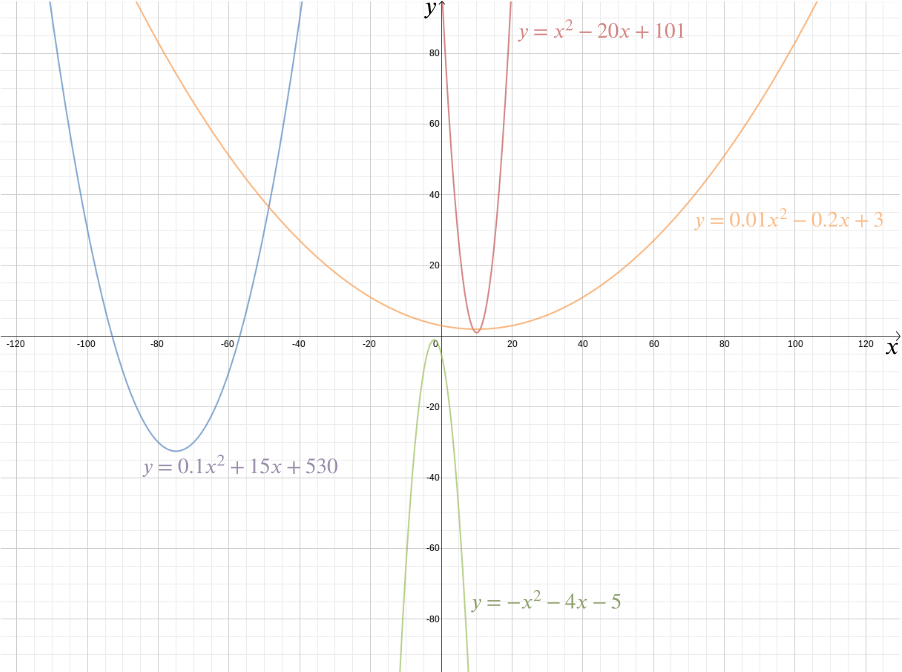
algebraické reprezentace umožňuje snadno odpovědět na celou řadu geometrické otázky. Vypracovat body na průsečíku řádku dána \ a parabola \(y = \frac{x^2}{2} – \frac{1}{2}\), jsme prostě na vědomí, že \(y\) souřadnice jakéhokoliv bodu \((x,y)\) leží na obou, musí splňovat obě rovnice, takže \ To dává \ Řešení kvadratické rovnice dostaneme \ a \, takže průsečíky jsou v \
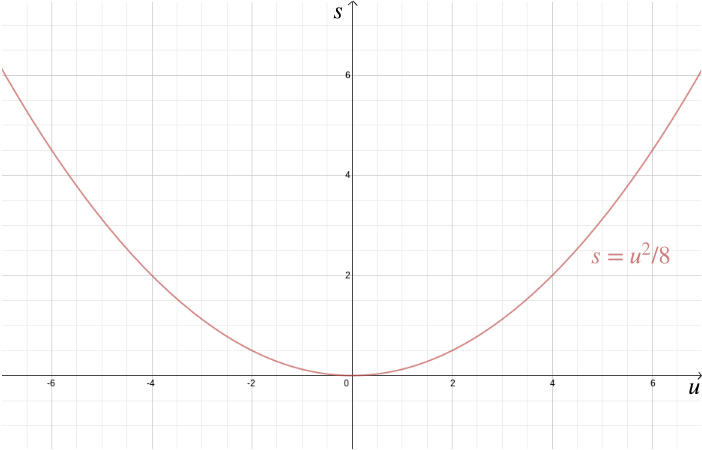
na Rozdíl od řešení geometrických problémů, Kartézské souřadnice také pomoci vizualizovat algebraické vztahy. Předpokládejme například, že auto jede rychlostí \(u\) a řidič brzdí, což má za následek konstantní zpomalení například \(-4\) metrů / sekund\(^2\). Brzdná dráha \(s\)—vzdálenost, auto kryty, než se to zastaví—je dána algebraickým vztahem \ Vykreslování pomocí Kartézských souřadnic přináší domů jen, jak je důležité zpomalit v městských oblastech, protože brzdná dráha se rychle zvyšuje s \(u\).
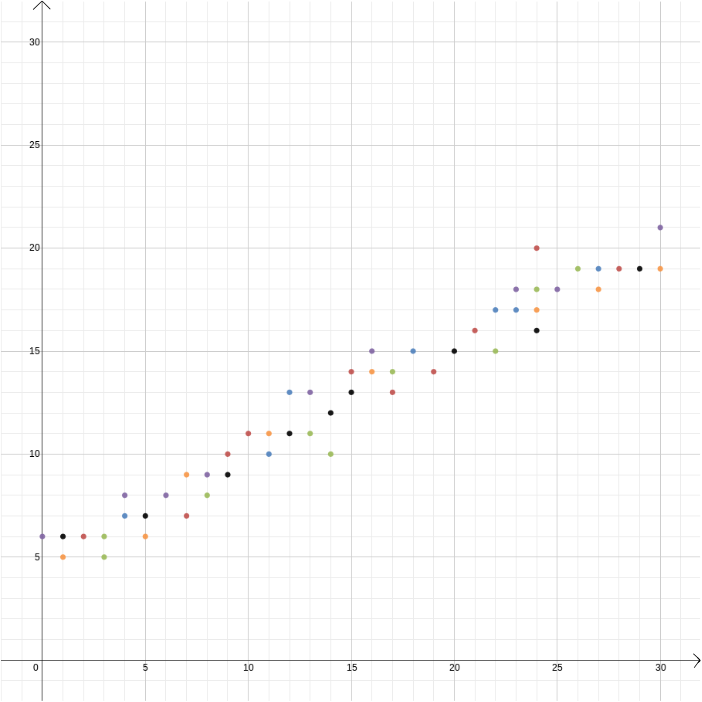
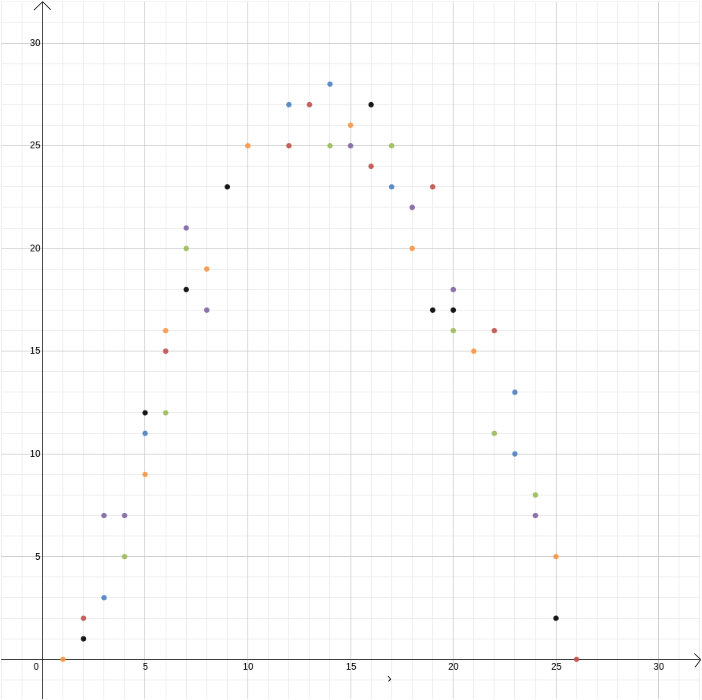
V tomto příkladu věděli jsme, že vztah mezi dvěma proměnnými, protože to lze odvodit ze zákonů fyziky. Ale kartézské souřadnice jsou také užitečné, když máte podezření, že dvě proměnné spolu souvisejí, ale nevíte jak. Předpokládejme, že si myslíme, že existuje vztah mezi ziskem prodejce zmrzliny a venkovní teplotou. Zjistit, co ten vztah může být, můžeme měřit teplotu a zisk více než, řekněme, v průběhu roku a pozemek hodnoty proti sobě, s teplotou zaznamenanou na \(x\)-osy a zisk na \(y\)-osa. Pak uvidíme, zda můžeme najít vzor. V prvním diagramu níže můžeme hádat, že vztah je lineární, a můžeme se pokusit najít přímku\, která nejlépe odpovídá našim datům (existují metody pro nalezení toho nejlepšího). Ve druhém diagramu níže můžeme hádat, že vztah je kvadratický a znovu se můžeme pokusit najít funkci\, která nejlépe vyhovuje datům.
kartézské souřadnice hrály významnou roli ve vývoji počtu ve druhé polovině 17. století. Počet umožňuje vypracovat atributy křivek, jako je jejich sklon v daném bodě nebo oblast oblasti, která leží mezi křivkou a osou \(x\). Ty mohou mít také fyzické interpretace. Například, pokud jsme pozemek vzdálenost auto putuje proti času, že byl na cestách, sklon výsledné křivky v daném čase—rychlost změny vzdálenosti s ohledem na čas—představuje rychlost, při které auto bylo cestování na ten okamžik v čase: je to derivace funkce, která nám dává vzdálenost v čase. Podívejte se také, Proč jsou přechody důležité v reálném světě?.
můžeme také jít do dimenze zvážením třetí osy kolmé na první dvě, kterou si můžete představit jako vycházející z vašeho listu papíru a směřující na vás. Pomocí takového trojrozměrného systému nyní můžete reprezentovat trojrozměrné objekty a vizualizovat, jak třetí proměnná \(z\) závisí na vašich prvních dvou, \(x\) a \(y\).
Tyto příklady by vám nějaký smysl, proč souřadnice staly se tak nepostradatelnou ve všech oblastech vědy, z fyziky, astronomie, a inženýrství, a také v aplikaci visual průmyslu k výrobě počítačové grafiky a počítačem generované obrazy, které obdivujeme ve filmech a hrách.
v samotné matematice spojení mezi algebrou a geometrií vyvrcholilo v celé oblasti zvané algebraická geometrie, která má vlastní fascinaci. Snad nejznámější výsledek, který vyplynul z této oblasti je velká Fermatova Věta, pojmenovaný po moderní Descartes, Pierre de Fermat, který také výrazně přispěl k rozvoji Kartézský souřadnicový systém. Fermat zvažoval otázku, která spojuje geometrii s teorií čísel. Podle Pythagoras teorém, pokud \(a\), \(b\) a \(c\) jsou strany pravoúhlého trojúhelníku a \(c\) je strana naproti pravému úhlu, pak \(a^2 + b^2 = c^2\). Existuje nekonečně mnoho trojic celých čísel \(a\), \(b\) A \(c\), které tento vztah uspokojují; \((3,4,5)\) je příkladem.
Nyní předpokládejme, že změníme exponent a zvážit výrazy jako \ a \ a obecněji \ kde \(n\) je přirozené číslo větší než \(2\). Můžeme stále najít kladná celá čísla \(a\), \(b\) A \(c\) uspokojující rovnici? Fermatova podezření, že nemůžeme a načmáral, jak moc v rozpětí jeho matematika text knihy, řekl, že má „úžasné důkaz“ pro to je skutečnost, kterou rozpětí bylo příliš úzký obsahovat.
že čmáranice bylo strašit matematiků pro více než 350 let. Teprve v roce 1994 byl matematik Andrew Wiles konečně oznámen správným důkazem tohoto zdánlivě neškodného výsledku. Wiles široce využíval algebraickou geometrii. Zvláště, on použil výsledky týkající se eliptických křivek popsal bodů v rovině, jejichž souřadnice splňují \ Descartes‘ rozjímání moucha má za sebou dlouhou cestu!
