Cesaro sčitatelnost

Existuje více než jeden způsob, jak součet nekonečné řady. Cesàro sumation umožňuje vypočítat součet sérií, které nemají součet v klasickém smyslu.

Předpokládejme, že máme nekonečnou řadu

$a_0 + a_1 + a_2 + \cdots$

n-tý částečný součet řady je dána tím,

$S_n = \sum_{i=0}^n a_i$

klasické součet řady, pokud existuje, je definován limit pro její částečné součty. To je,

$\sum_{i=0}^\infty a_i\stackrel{\text{def}}{=} \lim_{n\to\infty} \sum_{i=0}^n a_i$

Cesàro součtu má jiný přístup. Místo toho, aby limit částečných částek, bere limit průměrů částečných částek. Chcete-li být konkrétní, definovat

$C_n = \frac{S_0 + S_1 + S_2 + \ldots + S_n}{n}$

a definovat Cesàro sumační být limit Kn jako n jde do nekonečna. Pokud má řada součet v klasickém smyslu, má také součet ve smyslu Cesàro a limity jsou stejné. Ale některé série mají Cesàro součet, který nemají klasickou sumu. Nebo možná existují oba limity, ale mezistupně Cesàro summation jsou lépe chovány, jak uvidíme v příkladu níže.

Pokud se vám express Kn, pokud jde o původní podmínky, dostanete

$C_n = \sum_{i=0}^n \frac{n-i+1}{n+1} a_i$

jinými slovy, n Cesàro dílčí součet je reweighting klasické částečné součty, s hmotností mění jako funkce n. Všimněte si, že pro pevné i, zlomek vynásobením ai jde do 1, jak n se zvyšuje.

Fejér sumace a Gibbsův jev

Fejér sumace je Cesàro sumace aplikovaná na Fourierovu řadu. (Obyčejné) částečné součty Fourierovy řady poskytují nejlepší aproximaci funkce měřené normou nejmenších čtverců. Částečné součty Cesàro však mohou být kvalitativně spíše jako aproximovaná funkce. Ukážeme to níže čtvercovou vlnou.

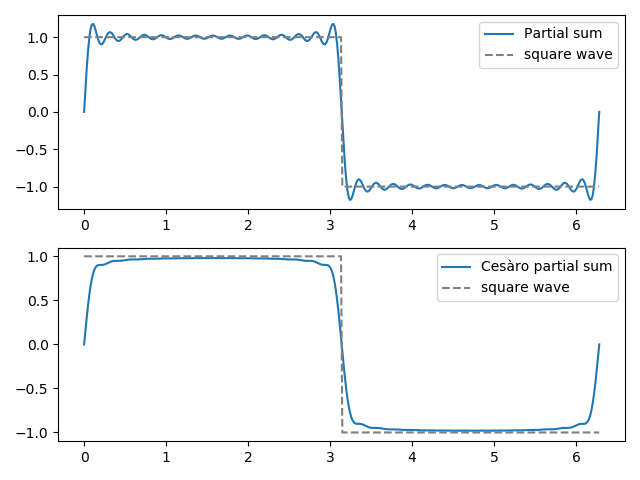
30. běžné dílčí součet ukazuje počátky Gibbsova jevu, „netopýří uši“ v horní části náměstí vlna a jejich zrcadlový obraz na dně. 30. Dílčí součet Cesàro je plynulejší a eliminuje Gibbsovy jevy poblíž diskontinuity ve čtvercové vlně.

více příspěvků Fourierovy řady

Fourierova-Besselova řada
protipříklad Dirichletova principu
oříznuté sinusové vlny

KGSAU

Cesàro shrnutí

Fejér sumace a Gibbsův jev

více příspěvků Fourierovy řady

Napsat komentář Zrušit odpověď na komentář